Н.И. НЕВЗОРОВ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению расчетно-графической работы

по дисциплине " Инженерная геодезия^"

на тему "Составление топографического плана

тахеометрической съемки"

для студентов строительных специальностей

всех форм обучения.

Ижевск 1999 г.

УДК 528.49

Составители: Н.И. Невзоров, к.т.н., доцент кафедры ГиСМ

Рецензенты: Н.Н. Рыбников, доц. каф. ГиТ

С.П. Макаров, ст. препод. каф. ГиСМ

Методические указания к выполнению расчётно-графической работы по дисциплине «Инженерная геодезия» на тему: «Составление топографического плана тахеометрической съёмки».

Печатается по решению методического совета ИС факультета

протокол № 5 от « 25 » января 1999 г.

Методические указания предназначены для студентов строительных специальностей всех форм обучения. В методических указаниях рассмотрен состав полевых и камеральных работ при топографической съёмке небольшого участка местности с целью проектирования зданий и сооружений, а также вопросы камеральной обработки результатов полевых измерений и составления топографического плана.

ВВЕДЕНИЕ.

Топографические планы необходимы проектным и строительным органи­зациям для разработки генеральных планов городов и поселков; проектов де­тальной планировки; проектирования линейных сооружений; составления разбивочных чертежей; решения задач вертикальной и горизонтальной планиров­ки; проектов реконструкции промышленных, сельскохозяйственных и граждан­ских объектов; составления исполнительных планов строящихся объектов; планов подземных коммуникаций и т.д.

Топографические съемки подразделяются на наземные и воздушные. К наземным методам съемок относятся:

• теодолитная;

• фототеодолитная;

• тахеометрическая;

• мензульная;

• нивелирование поверхности.

Если съемка выполняется с целью получения на плане взаимного поло­жения контуров местности, то она называется плановой. Если ставится цель по­лучить на плане не только контуры, но и рельеф местности, то такая съемка на­зывается топографической. В отдельных случаях заказчика интересует только рельеф местности. В этом случае съемка называется вертикальной.

Независимо от метода съемки всем им присущи одинаковые этапы работ, представленные в виде схемы.

Подготовительный период

Рекогносцировка местности и закрепление точек съемочного обоснования

Измерение горизонтальных и вертикальных углов, а также длин линий

Съемка контуров и рельефа местности

К амеральная обработка результатов измерений

Построение плана топографической съемки

Сравнение плана с местностью

Рис.1. Схема последовательности этапов работ при создании топографических планов.

В первой части предлагаемой методической разработки подробно рас­смотрены как полевые, так и камеральные работы при создании топографического плана методом теодолитно-тахеометрической съемки. Полученный план используется во второй части для составления разбивочного чертежа с целью перенесения осей сооружения на местность.

Методическая разработка не претендует на роль учебника и предусматри­вает, что студенты; прежде чем приступить к выполнению расчётно-графичеекой работы, проработали конспект лекций и учебники [1,2] .Рекомендуется после выполнения работы ответить на контрольные вопросы

1.Состав работ при создании съемочного обоснования.

После согласования участка строительной площадки и утверждения проекта изыскательских работ выполняют закрепление точек съемочного обоснования и привязку их к пунктам геодезической опорной сети. Наиболее распро­страненным методом создания съемочного обоснования является проложение теодолитно-высотных ходов в виде замкнутых полигонов с рассечкой их одним или несколькими диагональными ходами. В результате рекогносцировки местности уточняется положение точек съемочного обоснования. Основными кри­териями по выбору их местоположения являются:

• хороший обзор с них контуров и рельефа;

• удобство измерения углов и длин линий;

• сохранность точек.

Точки съемочного обоснования, в зависимости от предполагаемой про­должительности их сохранения, закрепляют деревянными кольями, металлическими штырями, насечками и окрасками на асфальте и других предметах.

Измерение длин линий выполняют механическими мерными приборами (рулетками, лентами) или светодальномерами с обеспечением точности не менее 1/2000, При этом длины линии должны находиться в пределах 40-150м. Измерения выполняют с контролем, т.е. в прямом и обратном направлении двумя мерными приборами. Для редуцирования их на горизонтальную плоскость измеряют вертикальные углы или превышения отрезков, углы наклона которых превышают 1°.

В отдельных случаях, чаще всего при проложении диагональных ходов, допускается измерение длин линий нитяным дальномером в прямом и обратном направлениях.

Горизонтальные углы измеряют теодолитом технической точности полным приемом при допустимых расхождениях между полуприемами 1°. Угловые невязки в замкнутых и разомкнутых полигонах не должны превышать 2t√n, где t-точность теодолита. Для обеспечения такого допуска необходимо обращать особое внимание на тщательность центрирования теодолита и визирных целей.

Превышения между точками съемочного обоснования могут быть изме­рены как методом геометрического нивелирования из середины, так и тригонометрическим нивелированием в прямом и обратном направлениях. Применение того или иного метода диктуется высотой сечения рельефа. Если h₀≥1м, то вы­бирают, как правило, тригонометрическое нивелирование. Во всех случаях все измерения необходимо выполнять с достаточным контролем и исключением из результатов измерений систематических погрешностей.

В методической разработке ниже рассмотрен пример камеральной обра­ботки результатов измерений и построения топографического плана на съемоч­ном обосновании, созданном в виде замкнутого полигона и диагонального хода (рис.2).

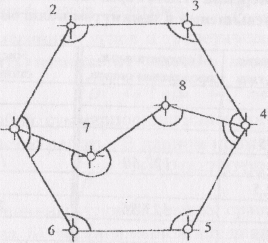
Рис.2. Схема съемочного обоснования

Точка 1 съемочного обоснования привязана к пунктам государственной геодезической сети и поэтому известны все три ее координаты Х₁, V₁, Н₁. Из­вестен также дирекционный угол α_1-2. Исходные координаты и угол ориентиро­вания выдает преподаватель.

В табл.1 приведены результаты измерений горизонтальных углов, длин линий и превышений в замкнутом полигоне. Горизонтальные углы измерены теодолитом 2ТЗОП полным приемом, длины линий - в прямом и обратном на­правлениях стальной 20-ти метровой лентой, а превышения.- геометрическим нивелированием из середины по двухсторонним рейкам. В таблице 2 приведены результаты измерений горизонтальных углов, длин линий и превышений в диа­гональном ходе. Горизонтальные углы измерены теодолитом 2ТЗОП полным приемом, а длины линий - нитяным дальномером в прямом и обратном на­правлениях. В таблице приведены их средние значения, редуцированные на го­ризонтальную плоскость по формуле

d = D cos² ν, (1)

где D – дальномерное расстояние;

ν – угол наклона.

Превышения в диагональном ходе измерены методом тригонометриче­ского нивелирования в прямом и обратном направлениях и вычислены по фор­муле:

D

2

h = sin2v+i, (2)

где i - высота теодолита над вершиной угла;

ν- высота наведения визирного луча на рейку.

В таблице приведены средние значения превышений.

Таблица 1.

Результаты измерения углов, горизонтальных длин линий

и превышении в замкнутом полигоне

№ вершин	Среднее значение измеренных углов	Горизонтальные проложения сторон	Число станций	Превышения, мм
6
1	151 32.5
		127.60	1	1856
2	106 14.5
		123.86	2	-784
3	119 46.5
		131.36	2	86
4	115 01.5
		125.35	2	659
5	134 41.0
		129.15	1	1090
6	92 46.0
		117.64	2	-2900
1

Таблица 2

Результаты измерения углов, горизонтальных длин линий

и превышений в диагональном ходе

№ вершин	Среднее значение измеренных углов	Горизонтальные проложения сторон, м.	Превышения, м
6
1	55 48.0
		86.9	9,14
7	279 22.5
		91.1	-2,16
8	81 31.5
		133.2	-5,84
4	75 50.0
5

2. Вычисление координат точек замкнутого теодолитного хода

2.1. Средние значения горизонтальных углов теодолитного хода из табл. 1 выписывают в колонку 2 ведомости вычисления координат (табл. 3) и подсчи­тывают сумму углов (_изм) в замкнутом полигоне. В рассматриваемом приме­ре эта сумма равна 720° 02,0'. Полученную сумму сравнивают с теоретической суммой углов (_теор ), которая вычисляется по формуле :

_теор =180° (n-2), (3)

где п  число измеренных углов,

В данном полигоне 6 углов, поэтому: _теор=180°(n-6)=720°00'. Раз­ность между суммой измеренных углов и теоретической суммой (то, что есть минус то, что должно быть) называется

угловой невязкой (f_)

f_=_изм -_теор (4)

которая представляет собой суммарное значение погрешностей измерения уг­лов и характеризует качество работы. В данном примере невязка равна:

f_=72002,0-72000,0=2,0.

Абсолютное значение величины угловой невязки сравнивают с предельно до­пустимой величиной (доп. f_ ), установленной для данного класса работ. Она определяется по формуле:

доп. f_ =2t√n, (5)

где, п количество измеренных углов,

t  точность теодолита.

В нашем примере: доп. f_ =1√6 = ±2,4'.

Так как f_< доп. f_, то измерения считаются удовлетворительными, а сле­довательно полученную невязку распределяют с обратным знаком в измерен­ные углы в виде поправок _ :

_ =−f_ /n (6)

Поправки _ округляют до 0,1', но сумма поправок должна точно равняться невязке f_ с противоположным знаком. Если f_ не делится ровно на п, то большие поправки вводят в утлы с короткими сторонами. Значения поправок записывают над измеренными углами. Затем вычисляют исправленные углы по формуле:

_испр=_изм+_

и записывают их в колонку (3) ведомости. Сумма исправленных углов должна равняться теоретической сумме.

2.2. По исправленным значениям углов и дирекционному углу исходной линии 1-2 вычисляют дирекционные углы всех линий теодолитного хода как

α_посл=α_пред.+180º- β_испр (7)

то есть дирекционный угол последующей линии равен дирекционному углу предыдущей линии плюс 180°, минус, исправленный угол, право по ходу лежа­щий. Эта связь хорошо прослеживается на рис.3, где показана схема вычисле­ния α_1-3

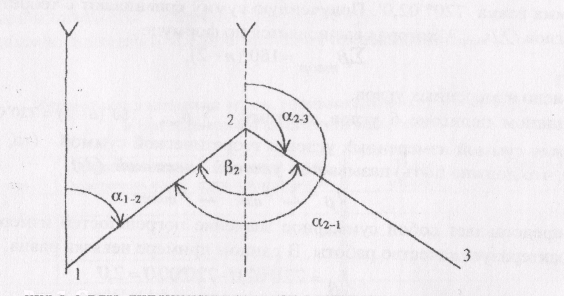
Рис.3. Связь дирекционных углов с горизонтальными углами.

Значение дирекционного угла исходной линии (1-2) в данном примере равно 18⁰31,0´, а исправленное значение угла β₂=106º14,1´. Тогда дирекционный угол стороны α_2-3 равен:

α_2-3=18⁰31,0´+180°00.0´-106°I4.1´=92°16.9´,

а дирекционный угол α_3-4 равен:

α_3-4 =92° 16,9´+180°00.0´ -119°46,2´ = 152º30,7´.

Аналогичным образом вычисляют дирекционные углы всех других линий полигона. Вычисления дирекционных углов контролируют тем, что по дирекционному углу стороны (6-1) и углу на станции 1 вычисляют дирекционный угол исходной (заданной) стороны (1-2). Расхождений не должно быть. Прове­ренные значения дирекционных углов линий теодолитного хода выписывают в соответствующую колонку ведомости вычисления координат.

2.3. Вычисляют горизонтальные проложения линий (табл.1) по формуле:

d =√D²-h², (8)

где d — горизонтальное проложение длины линии;

D — среднее измеренное значение длины линии;

h — превышения между концами линии.

Рис.4.Приведение длин линий к горизонту.

Вычисленные значения горизонтальных проложений длин линий выписы­вают в колонку (5) ведомости (табл.3).

Примечание. В рассматриваемом примере в табл.1 и 2 значения длин ли­ний даны на горизонтальной плоскости.

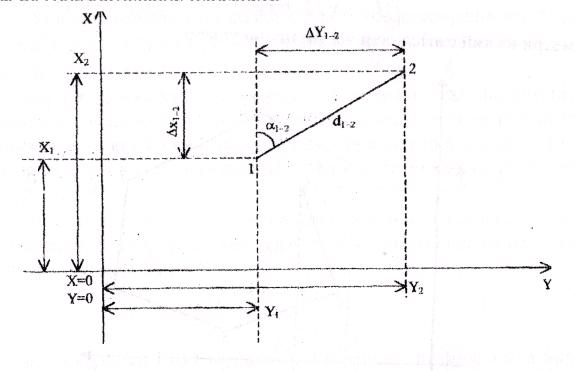
Рис. 5. Геометрическая схема вычисления приращений координат

2.4 . По горизонтальным проложениям длин линий и их дирекционным углам вычисляют приращения координат (∆х и ∆у) по формулам (рис.5):

∆х = d cos α, (9)

∆y= d sin α.

Контроль d =√∆х² +∆у².

Приращения вычисляют на калькуляторе или ПК. Вычисленные прира­щения координат округляют до 0,01 м и выписывают в колонки 6 и 7 ведомости (табл.3). В зависимости от того в какой четверти находятся значения α_i линий теодолитного кода приращениям координат приписывают знаки "плюс" или "минус".

Так как полигон замкнутый, то с теоретической точки зрения сумма приращений координат по обеим осям равны нулю (Σ∆х_теор и Σ∆у_теор). Вслед­ствие погрешностей измерения углов и линий этого, как правило, не бывает, т.е. Σ∆Х≠0, Σ∆Y≠0, а следовательно:

Σ∆Χ= f_{Χ ,} (10)

Σ∆Y= f_{Y ,}

Значения f_Χ и f_Y называются невязками по соответствующим осям коор­динат. Они являются количественными характеристиками точности измерения углов и длин линий и служат для оценки качества выполненных измерений. По этим невязкам вычисляют абсолютную линейную невязку теодолитного хода f_d по формуле:

f_d=√f_x²+ f_y² (11)

Геометрический смысл ее показан на рисунке 6.

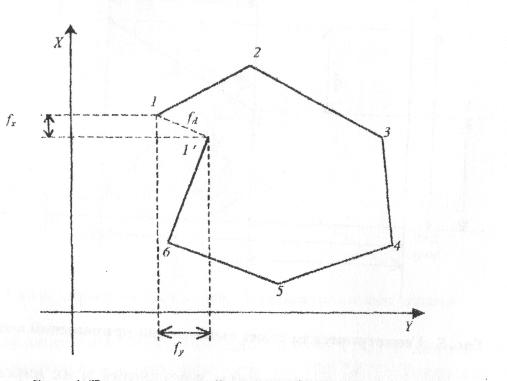
Рис. 6. Геометрический смысл абсолютной невязки.

По данным нашего примера (см. табл. 3), имеем:

f _d =√(-0.22)² + 0.16² = 0.27м

Абсолютная линейная невязка недостаточно характеризует точность ли­нейных измерений. Более удобной характеристикой для этих целей служит от­носительная невязка, т.е. f_d/Σd. В геодезии относительную невязку записывают всегда в виде простой дроби, в числителе которой единица. Если относительная невязка меньше 1/2000, то измерения и вычисления признают удовлетворитель­ными, а значения f_x и f_y считают допустимыми. Относительная невязка, полу­ченная в нашем примере, равна 1:2800, что меньше допустимой 1:2000. Так как условие выполнено, то невязки необходимо распределить в приращения ко­ординат в виде поправок пропорционально длинам сторон, т.е.

f_x

Σd

_∆Χi =- d_i ,

f_y

(12)

Σd

_∆Yi =- d_i .

Например, в приращение ∆х_1-2 поправка равна _∆X1-2 = +0,04м, а в при­ращение ∆у_1-2 равна _∆Y1-2 = -0,03м.

Так как поправки в приращения координат имеют не более двух значащих цифр, то периметр полигона (Σd) и длины линий в формуле (12) достаточно взять с округлением до сотен метров.

Аналогично вычисляют поправки и в остальные приращения ∆x и ∆y. Ал­гебраическая сумма поправок в приращения должна быть равна величине не­вязки, взятой с обратным знаком, т.е. _∆x = −f_x, _∆y=−f_y.

Поправки в приращения координат выписывают над соответствующими приращениями в ведомости (табл.3) и затем вычисляют исправленные прира­щения. Алгебраические суммы исправленных приращений координат в замкну­том теодолитном ходе должны быть равны теоретической сумме, т. е. ∆x_исп=0, ∆y_исп=0

2.5. По заданным координатам начальной точки и по исправленным зна­чениям приращений координат вычисляют координаты остальных точек теодо­литного хода по формулам:

Y_i= Y_i−1+ ∆y_i−1,i (13)

X_i= X_i−1+ ∆x_i−1,i

и записывают в колонки 10-11 ведомости. Контролем правильности вычисления координат является получение координат начальной точки 1.

З.Вычисление координат точек диагонального тахеометрического хода

Так как диагональный ход опирается на точки замкнутого полигона, то исходными данными для вычислительной обработки являются: Х₁, Y₁, X_4, Y1,α_6-1, α_4-5.

Обработка результатов измерений диагонального хода принципиально не отличается от рассмотренной выше схемы обработки замкнутого полигона. Особенности заключаются в следующем.

3.1.Для вычисления угловой невязки теоретическую сумму углов (если измерены правые углы) находят как

Σβ_теор= n ·180º+(α_н - α_к), (14)

где п - число измеренных углов;

α_н - дирекционный угол начальной стороны (6-1),

α_к - дирекционный угол конечной стороны (4-5).

Примечание. Если α_н меньше α_к, то к α_н необходимо прибавить 360°.

Угловая невязка равна f_β=β_пр.−β_теор.

Применительно к рассматриваемому числовому примеру α_н =^:350º03.1; α_к =217°29.5', а следовательно угловая невязка равна :

f_β=492°32.0-4∙180º+(350º03,1-217°29.5)=-1.6

Допустимую угловую невязку в диагональном ходе принимают равной 3t√n. Применительно к примеру don.f_β = 1,5√4 = ±3.0.

3.2.Невязки f_x и f_y вычисляют по формулам:

f_x=∆x_выч−(X_к− Х_н) (15)

f_y=∆y_выч −(Y_к−Y_н),

где Х_н,Y_н- координаты начальной точки хода (точка1);

Х_к,Y_к- координаты конечной точки кода (точка 4).

Координаты Х_н, Y_н,Y_к, X_к берут из таблицы 3 и округляют до 0,1 м. При изме­рении длин линий в ходе нитяным дальномером допустимая абсолютная линей­ная невязка не должна превышать:

Σd

400√n

f_d= (16)

где n - число сторон хода;

d- длина хода.

Для нашего примера d=311.2м, п=3. По формуле (16) доп.f_d=0.4м, а по результатам измерений f_d=0.1 м. Следовательно, полевые измерения выполнены удовлетворительно, а в вычислительном процессе отсутствуют грубые погреш­ности.

Дальнейший ход обработки результатов измерений в диагональном ходе не отличается от изложенного в § 2. Контролем правильности вычислений слу­жит получение координат X и Y вершины №4.

№ вер-шин	Измеренные углы	Исправлен-ные углы	Дирекцион-ные углы	Горизонталь-ные проложения	Вычисленные приращения координат		Исправленные приращения координат		Координаты		№вер- шин
	β		α	d,м	∆x,м	∆y,м	∆x,м	∆y,м	X,м	Y,м
1	2	3	4	5	6	7	8	9	10	11	12
1	-0.4 151°32.5´	151°32.1´			+0.04	-0.03			500.00	500.00	1
	-0.4		18°31.0´	127.60	120.99	40.52	121.03	40.49
2	106°14.5´	106°14.1´			+0.04	-0.02			621.03	540.49	2
	-0.3		92°16.9´	123.86	-4.93	+123.76	-4.89	123.74
3	119°46.5´	119°46.2´			+0.04	-0.03			616.14	664.23	3
	-0.3		152°30.7´	131.36	-116.53	60.63	-116.49	60.60
4	115°01.5´	115°01.2´			+0.04	-0.03			499.65	724.83	4
	-0.3		217°29.5´	125.35	-99.46	-76.29	-99.42	-76.32
5	134°41.0´	134°40.7´			+0.03	-0.03			400.23	648.51	5
	-0.3		262°48.8´	129.15	-16.16	-128.14	-16.13	-128.17
6	92°46.0´	92°45.7´			+0.03	-0.02			384.10	520.34	6
			350°03.1´	117.64	115.87	-20.32	115.90	-20.34
1									500.00	500.00	1

Ведомость вычисления координат замкнутого полигона. Таблица 3.

_изм = 720°02.0´ d = 754.96 м ∆x_выч.= -0.22 м ∆y_выч.= +0.16 м

_теор = 720°00.0´ f_x=-0.22 м f_y= +0.16 м

f_= +2 f_абс.=√f_x² +f_y²= 0.27 м

_доп.f_= +2.4 f_абс./d=0.27/754.96=1/2800<1/2000

№ вер-шин	Измеренные углы	Исправлен-ные углы	Дирекцион-ные углы	Горизонталь-ные проложения	Вычисленные приращения координат		Исправленные приращения координат		Координаты		№ вер- шин
	β		α	d,м	∆x,м	∆y,м	∆x,м	∆y,м	X,м	Y,м
1	2	3	4	5	6	7	8	9	10	11	12
6											6
	+0.4		350°03.1´
1	55°48.0´	55°48.4´							500.00	500.00	1
	+0.4		114°14.7´	86.9	-35.7	79.2	-35.7	79.2
7	279°22.5´	279°22.9´							464.3	579.2	7
	+0.4		14°51.8´	91.1	88.0	23.4	88.0	23.4
8	81°31.5´	81°31.9´				-0.1			522.3	602.6	8
	+0.4		113°19.0´	133.1	-52.7	122.3	-52.7	122.2
4	75°50.0´	75°50.4´							499.6	724.8	4
5			217°29.5´
											5

Ведомость вычисления координат точек диагонального хода. Таблица 4.

_выч = 492°32.0´ d = 311.2 м ∆x_выч.= -0.4 м ∆y_выч.=224.9 м

 _теор =α_5,1 – α_3,2 +180ºп =492°33.6´ ∆x_теор.= -0.4 м ∆y_теор.= 224.8 м

f_= -1.6 f_x= 0.0 м f_y=0.1 м

_{д оп.}f_= 3t√n =±2.0, f_d=√f_x² +f_y²= ±0.1 м

где n число углов _доп.f_d=Σd/400√n= ±0.4 м

4. Вычисление высот точек съемочного обоснования.

Полученные координаты X и Y точек съемочного обоснования позволя­ют построить контурный план местности. Если ставится задача показать на нем и рельеф, то необходимо дополнительно определить еще и высоты точек съе­мочного обоснования. Это возможно выполнить юга геометрическим, или три­гонометрическим нивелированием Выбор того или иного способа зависит от требуемой точности изображения рельефа.

В данной разработке по замкнутому полигону проложен ход геометриче­ского нивелирования технической точности, а по диагональному, ход триго­нометрического нивелирования

Геометрическое нивелирование выполнено способом из середины по двухсторонним рейкам трехметровой длины. Контроль на станции осуществля­ли сравнением пяток реек и по разностям превышений, полученных из измере­ний по черной и красной сторонам реек. Средние значения превышений приве­дены таблице 1.

При проложении диагонального хода длины сторон измерены нитяным дальномером в прямом и обратном направлениях, углы наклона, при двух по­ложениях вертикального круга также в прямом и обратном направлениях. Контроль измерения углов наклона осуществлялся по постоянству значения места нуля и размаху его колебания. Высота наведения соответствовала высоте инст­румента Расхождение превышений, полученных из прямого и обратного изме­рения, не превышало 4см на 100м длины линии.

Перед нивелированием точек съемочного обоснования выполняют его привязку к реперу, то есть к закрепленной точке местности с известной высо­той. В данной работе к реперу привязана точка I съемочного обоснования. Зна­чение высоты этой точки выдает преподаватель.

4.1. Вычисление высот точек съемочного обоснования в замкнутом полигоне

Вычислительную обработку результатов нивелирования точек замкнутого полигона выполняют в следующей последовательности (табл. 5).

4 1.1.Находят сумму средних превышений h_ср и сравнивают ее с теоре­тической. В замкнутом полигоне ее значение равно нулю. Таким образом, сумма измеренных средних превышений и есть невязка хода, f_h =h_ср

В рассматриваемом примере f_h=7 мм. (табл. 5). Невязка характеризует ка­чество измерений, поэтому ее сравнивают с допустимой (доп. f_h), которая зави­сит от класса нивелирования. Для технического нивелирования доп. f_h.=30 мм √d (км), где d − периметр полигона.

Таблица 5 .

Ведомость вычисления высот в замкнутом полигоне.

№ точек	п	hср.,мм	δh,мм	hиспр., мм	H,м
1					103.210
	1	+1856	-1	1855
2					105,065
	2	-784	-1	-785
3					104.280
	2	+86	-1	+85
4					104,365
	2	+659	-1	+658
5					105.023
	1	+1090	-1	+1089
6					106.112
	2	-2900	-2	-2902
1					103.210

h_ср. =7мм; fh=7мм; доп.f_h= ± 26мм.

В рассматриваемом примере периметр равен 0.75км, а, следовательно, доп.f_h=± 26мм. Полученная невязка попадает внутрь интервала допустимой, следовательно, измерения выполнены удовлетворительно.

4.1.2.Распределяют полученную невязку fh, пропорционально числу стан­ций с округлением до мм.

_h=-f_h/n. (17)

В нашем примере _h =-7мм/10= 0.7мм. Округляя _h до мм необходимо обяза­тельно выполнить условие:

_h =-f_h

4.1.3.Вычисляют исправленные превышения h_ucnp. как

h_ucnp=h_cp+_h.

Контролем правильности вычисления служит равенство нулю суммы ис­правленных превышений, т.е. h_uспp.=0. Далее вычисляют высоты точек теодо­литного хода

Н₂=Н₁ +h_{испр.(1-2)}

Н₃=Н₂+h_{испр.(2-3)} (18)

………………………

Н₁=Н₆+h_{испр.(1-6).}

Таким образом, в конце вычислений снова приходят к высоте исходной точки. Это служит контролем правильности вычислений.