Домашнее задание №3 для потока ТОА-224, 225, 227, 228 и МСС-226 (4 семестр, 2011-2012 учебный год)

З а д а н и е 1. Самостоятельно изучить тему: «Комплексные числа и работа с ними». Написать конспект.

З а д а н и е 2. Выполнить расчетное задание по теме «Представление синусоидальных функций комплексными числами и векторами на комплексной плоскости» (стр. 13).

Срок сдачи: до 20 апреля 2012 года.

Примечание: Для выполнения расчетного задания использовать теоретический материал, приведенный тексте задания и материал лекций по теме «Представление синусоидальных функций с помощью комплексных величин» и «Векторные диаграммы».

Комплексные числа и работа с ними

Введение понятия комплексного числа. Представление комплексного числа на плоскости

Комплексные числа являются расширением множества действительных чисел. В результате расширения множества действительных чисел было введено понятие мнимой единицы , которая существует на множестве комплексных чисел, но не существует на множестве действительных. Мнимая единица удовлетворяет равенству:

(1)

Комплексное число можно представить в виде:

(2)

где носит название действительной части или реальной части и обозначается , а носит название мнимой части и обозначается как .

Пример 1. Для каждого из заданных комплексных чисел найти действительную и мнимую части.

1). ;

Действительная часть: ;

Мнимая часть: .

2).

Действительная часть: ;

Мнимая часть: .

3).

Действительная часть: ;

Мнимая часть: .

4)

Действительная часть: ;

Мнимая часть: .

5).

Действительная часть: ;

Мнимая часть: .

Графически все множество действительных чисел можно представить на бесконечной числовой прямой, при этом комплексные числа можно трактовать как расширение числовой прямой до комплексной плоскости, а каждое комплексное число можно представить как точку на комплексной плоскости (рис. 1). При этом все множество действительных чисел будет представляться прямой на комплексной плоскости.

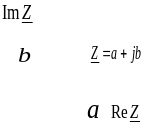
Рис. 1: Представление комплексного числа на плоскости

Комплексная плоскость делится прямыми реальной части (прямой действительных чисел) и прямой мнимых чисел на четыре четверти. Любое комплексное число ,будет представляться точкой на комплексной плоскости с координатами и . Если число не содержит мнимой части, то оно действительное и находится на прямой , а если число не содержит реальной части, то оно называется чисто мнимым и находится на оси .

Модуль и фаза комплексного числа

Если из начала координат комплексной плоскости к точке восстановить вектор, то можно вычислить длину этого вектора как

(3)

— действительное число, характеризующее длину вектора, и называется модулем комплексного числа. При этом сам вектор комплексного числа повернут относительно оси на некоторый угол , называемый фазой (аргументом) комплексного числа. Связь реальной и мнимой частей комплексного числа с его амплитудой и фазой представлено следующим выражением:

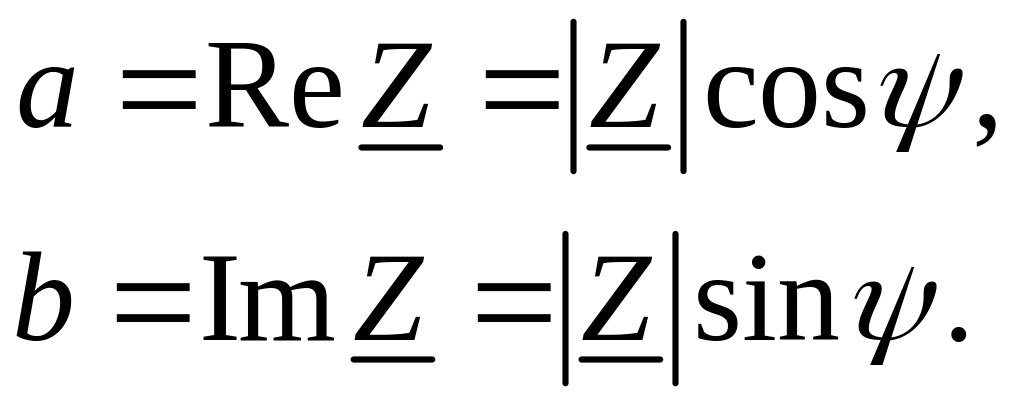(4)

Тогда комплексное число можно представить в тригонометрической форме:

(5)

Связь угла поворота вектора комплексного числа с реальной и мнимой частью комплексного числа:

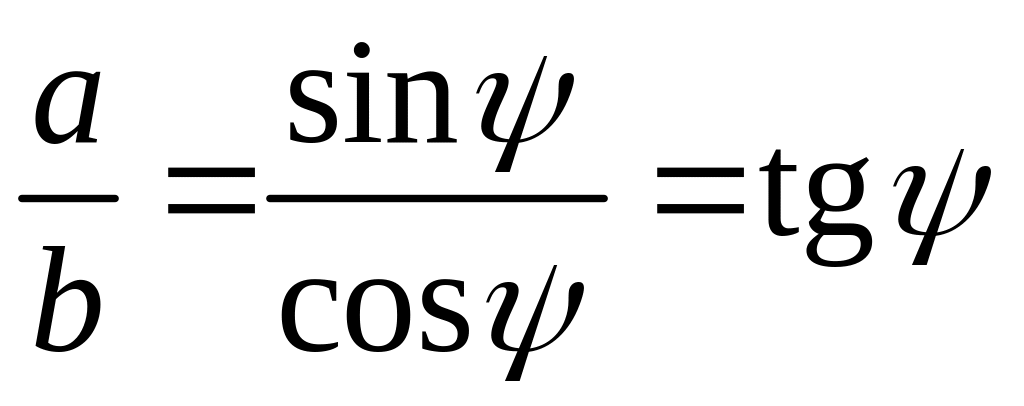(6)

тогда

, (7)

где учитывает четверть комплексной плоскости, в которой расположено число :

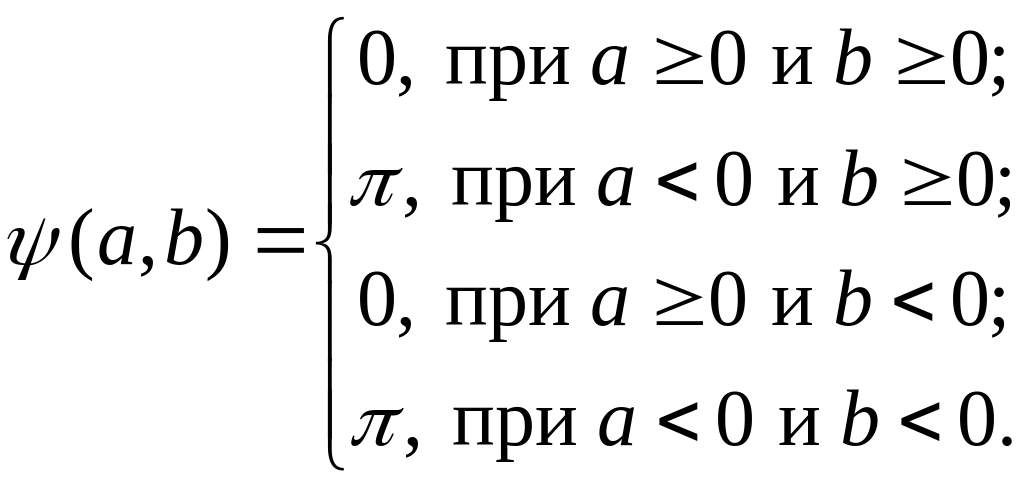(8)

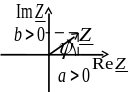
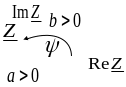
а) б)

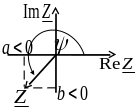
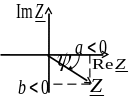
в) г)

Рис. 2: Вычисление угла поворота вектора комплексного числа

Для того чтобы понять смысл функции рассмотрим четыре варианта как это показано на рисунке 2.

Рисунок 2.а. , и , вектор в первой четверти плоскости. В этом случае .

Рисунок 2.б. , и , вектор во второй четверти плоскости. В этом случае. .

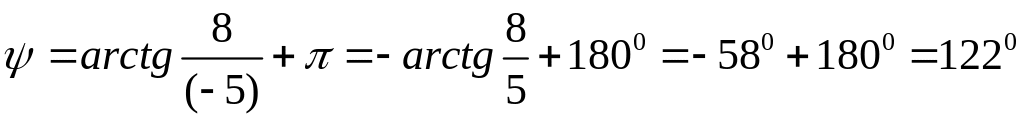Рисунок 2.в. , и вектор в третьей четверти плоскости. В этом случае .

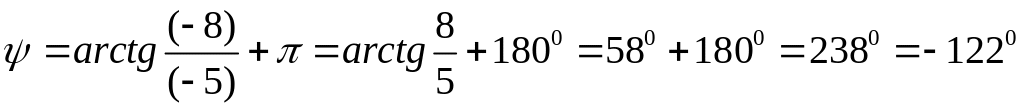Рисунок 2.г. , и вектор в четвертой четверти плоскости. В этом случае

.

Показательная форма комплексного числа. Существует также показательная форма комплексного числа связанная с тригонометрической по формуле Эйлера:

. (9)

Рассмотрим более подробно мнимую единицу в четной и нечетной степенях. Выражение (1) задало , тогда , в свою очередь . Таким образом можно рекуррентно записать:

. (10)

Построим аналогичным образом рекуррентное соотношение для нечетных степеней: тогда , в свою очередь , получим:

(11)

Сделаем несколько важных замечаний.

Замечание 1:

(12)

Замечание 2:

. (13)

Замечание3:

. (14)

Формы записи комплексного числа. Любое комплексное число можно записать в одной из форм:

• алгебраической: ;

• тригонометрической ;

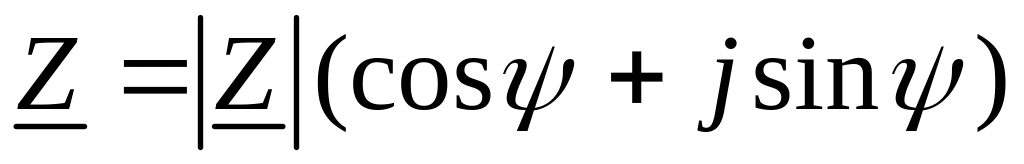• показательной .

Перевод из одной формы записи в другую определяется формулами, приведенными выше. Для упрощения перевода из одной формы в другую изобразим комплексное число на комплексной плоскости (рис. 3).

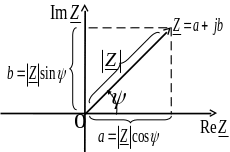
Рис. 3. Различные формы записи комплексного числа

Из рисунка легко получить переход от одной формы записи комплексного числа в другую. Например,

- из алгебраической – в показательную

,

где

- из показательной – в алгебраическую:

и т. д.

Перевод из одной формы записи в другую необходим при аналитических расчета с комплексными числами. Рассмотрим операции с комплексными числами.

Пример 2. Задано комплексное число . Представить его в тригонометрической и показательной формах.

Решение

Модуль комплексного числа

.

Фаза (аргумент):

.

Тригонометрическая форма:

.

Показательная форма:

.

Пример 3. Задано комплексное число . Представить его в тригонометрической и показательной формах.

Решение

Модуль комплексного числа

.

Фаза (аргумент):

.

Тригонометрическая форма:

.

Показательная форма:

.

Пример 4. Задано комплексное число . Представить его в тригонометрической и показательной формах.

Решение

Модуль комплексного числа

.

Фаза (аргумент):

.

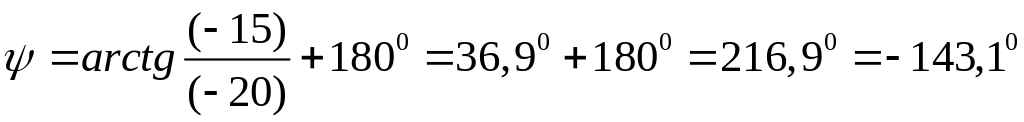Тригонометрическая форма:

.

Показательная форма:

.

Пример 5. Задано комплексное число . Представить его в алгебраической форме.

Решение

Алгебраическая форма:

.

Операции над комплексными числами. Сложение комплексных чисел.

Сумма двух комплексных чисел и есть также комплексное число :

. (15)

Как следует из выражения (15) при сложении комплексных реальные и мнимые части комплексного числа также складываются.

На комплексной плоскости операцию сложения можно реализовать как сложение векторов комплексных чисел по правилу параллелограмма (рис. 4).

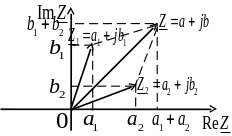
Рис. 4 Сложение комплексных чисел

Операции над комплексными числами. Вычитание комплексных чисел.

Разность двух комплексных чисел и есть также комплексное число :

. (15)

Как следует из выражения (15) при вычитании комплексных чисел реальные и мнимые части комплексного числа также вычитаются.

На комплексной плоскости операцию вычитания можно реализовать как вычитание векторов комплексных чисел по правилу параллелограмма (рис.5). На первом шаге из вектора формируется вектор , после чего вектор складывается с вектором по правилу параллелограмма.

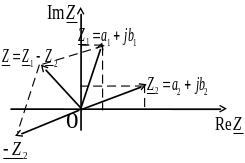
Рис. 5. Вычитание комплексных чисел