
- •Вопросы к экзамену
- •[Править]Шаг 1: Формирование таблицы шифрования[2]
- •[Править]Латинский алфавит
- •[Править]Русский алфавит[3]
- •[Править]Шаг 2: Принцип шифрования
- •[Править]Метод 1
- •Шифр Гронсфельда
- •Взлом полиалфавитных шифров
- •Гаммирование
- •Рекуррентный генератор последовательности чисел (ргпч)
- •Гаммирование с обратной связью
- •Выработка имитовставки
- •Алгоритм создания открытого и секретного ключей
- •Типы угроз для парольной системы.
- •Функции Службы информационной безопасности предприятия
Алгоритм создания открытого и секретного ключей
RSA-ключи генерируются следующим образом:[14]
Выбираются два различных случайных простых числа
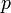 и
и 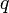 заданного
размера (например, 1024 бита каждое).
заданного
размера (например, 1024 бита каждое).Вычисляется их произведение
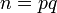 ,
которое называется модулем.
,
которое называется модулем.Вычисляется значение функции Эйлера от числа
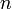 :
:
![]()
Выбирается целое число
 (
(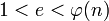 ), взаимно
простое со
значением функции
), взаимно
простое со
значением функции  .
Обычно в качестве
берут
простые числа, содержащие небольшое
количество единичных бит в двоичной
записи,
например, простые числа
Ферма 17,
257 или 65537.
.
Обычно в качестве
берут
простые числа, содержащие небольшое
количество единичных бит в двоичной
записи,
например, простые числа
Ферма 17,
257 или 65537.Число называется открытой экспонентой (англ. public exponent)
Время, необходимое для шифрования с использованием быстрого возведения в степень, пропорционально числу единичных бит в .
Слишком малые значения , например 3, потенциально могут ослабить безопасность схемы RSA.[15]
Вычисляется число
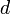 , мультипликативно обратное
к числу
по
модулю
,
то есть число, удовлетворяющее условию:
, мультипликативно обратное
к числу
по
модулю
,
то есть число, удовлетворяющее условию:
![]() .
.
Число называется секретной экспонентой. Обычно, оно вычисляется при помощи расширенного алгоритма Евклида.
Пара ![]() публикуется
в качестве открытого
ключа RSA (англ. RSA
public key).
публикуется
в качестве открытого
ключа RSA (англ. RSA
public key).
