1.3 Задание на расчет электромагнитных процессов в катушке

зажигания

Целью расчета переходных процессов в системе зажигания является расчет тока i₁(t), напряжений u_L(t), u_С(t), u₂(t) в общем виде и численно классическим и операторным методом для двух этапов по схемам рис.2 и рис.3. Переходные процессы рассчитываются для интервала времени (0–t_ЗАM, t_3АM - время накопления энергии магнитного поля) по схеме рис.2 и для интервала времени (0—t_РАЗ, t_РАЗ – время в течении которого ключ S разомкнут, в течении этого времени формируется высоковольтный импульс напряжения), по схеме рис.3. Курсовая работа должна быть оформлена в соответствии с требованиями ГОСТа по оформлению документов [2]. При расчете переходных процессов на первом и втором этапах отсчет времени следует начинать с нуля. Варианты индивидуальных заданий на курсовую работу по первой части даны в таблице 1.

1.4 Порядок расчета переходных процессов в катушке зажигания в режиме холостого хода (х.Х.)

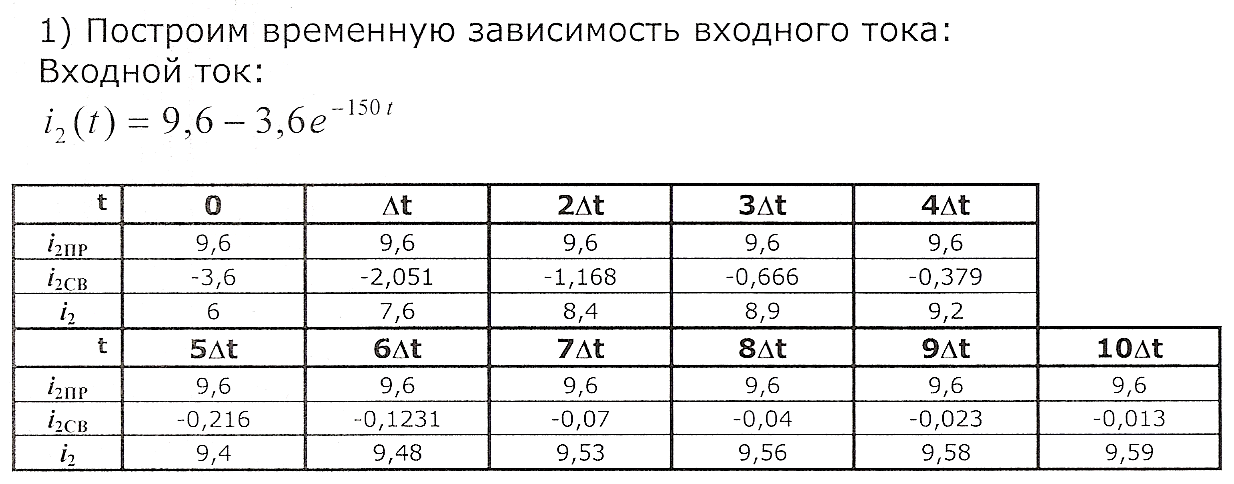
1. Производим расчет и определяем характер нарастания тока i₁(t) в первичной обмотке w₁ на первом этапе переходного процесса (рис.2) за время от 0 до t_H (t_H = t_ЗАMK – время накопления энергии магнитного поля в катушке зажигания, указано в таблице № 1 для варианта индивидуального задания).

2. Осуществляем расчет временных зависимостей u₁(t) и u₂(t).

3. По полученным выражениям i₁(t), u₁(t) и u₂(t) строим графики в одном временном масштабе с совмещением начала координат. Мгновенные значения напряжений и токов определяются в моменты времени 0; lt; 2t ... 10t.( .

4. Рассчитываем ход переходного процесса на втором этапе, т.е. после размыкания ключа S с учетом начального значения тока в катушке w₁ (i₁ = i_H). В результате расчета необходимо получить выражения для i₁(t), u_L(t), u_С(t), u₂(t), характеризующих переходной процесс на втором этапе.

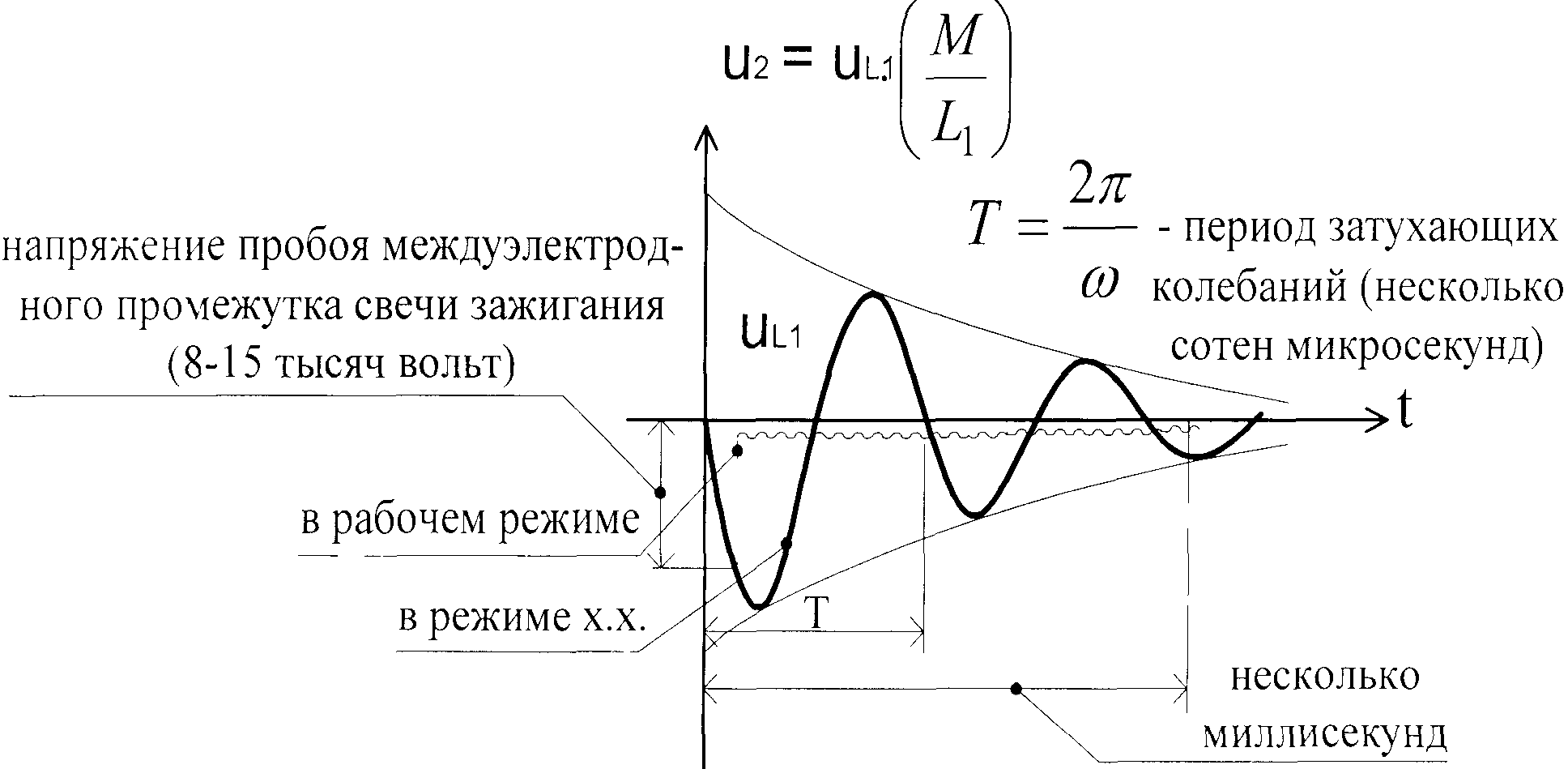
Рис.4

5. По полученным выражениям строим графики временных зависимостей в одном временном масштабе, совмещая начала координат, на одном листе. Мгновенные значения вычисляются в моменты времени 0; lt; 2t; 3t;....10t,

где  = (т.е. каждый из первых 3-х периодов 1 =— затухающих синусоидальных колебаний делят на 10 частей).

После построения кривой напряжения на вторичной обмотке u₂(t) в режиме холостого хода, на эту кривую пунктиром наносим реальную кривую для рабочего режима в условиях электрического пробоя межэлектродного пространства свечи зажигания, как показано на рис. 4.

Таблица 1. Варианты индивидуальных заданий на курсовую работу по первой

части.

№ зада-ния	Исходные данные для расчета
	Е, (В)	R, (Oм)	L1, мГн	W1	W2	C, мкФ	tзам., с	tраз. , с	М, Гн
1	12,6	2	10	310	23000	0,25	0,025	0,015	0,55
2	12,6	2,5	11	250	38000	0,25	0,025	0,015	0,25
3	12,6	2,5	10	310	23000	0,25	0,025	0,015	0,55
4	12,6	2,2	10	310	23000	0,25	0,025	0,015	0,55
5	12,6	2,2	12	250	38000	0,33	0,025	0,015	0,27
6	12,6	2,2	12	250	38000	0,33	0,025	0,015	0,27
7	12,6	2,1	9	300	25000	0,33	0,025	0,015	0,62
8	12,6	2,4	9	300	25000	0,3	0,025	0,015	0,62
9	12,6	2,4	9	300	26000	0,3	0,025	0,015	0,67
10	12,6	2,3	8	300	27000	0,3	0,025	0,015	0,64
11	12,6	2,3	8	310	25000	0,3	0,025	0,015	0,52
12	12,6	2,3	8	250	37000	0,4	0,025	0,015	0,17
13	12,6	2,5	11	250	35000	0,4	0,025	0,015	0,21
14	12,6	2	11	250	34000	0,4	0,025	0,015	0,2
15	12,6	2	11	250	33000	0,4	0,025	0,015	0,19
16	12,6	2	10,5	250	32000	0,25	0,025	0,015	0,17
17	12,6	1,8	10,5	270	38000	0,25	0,025	0,015	0,2
18	12,6	1,9	11,5	280	37000	0,3	0,025	0,015	0,2
19	12,6	2	9,5	290	36000	0,3	0,025	0,015	0,14
20	12,6	2	9,5	290	35000	0,3	0,025	0,015	0,13
21	12,6	2,1	9,5	300	25000	0,35	0,025	0,015	0,36
22	12,6	2,0	9,0	270	27000	0,3	0,025	0,015	0,32
23	12,6	1,6	8,5	250	30000	0,25	0,025	0,015	0,3
24	12,6	1,8	8,0	230	26000	0,2	0,025	0,015	0,25

Примечание: tзам – время, в течении которого ключ S замкнут; tраз- время в течении которого ключ S разомкнут.

После построения кривой напряжения на вторичной обмотке u₂(t) на втором этапе переходного процесса, определяющий характер изменения напряжения на вторичной обмотке в режиме холостого хода, на эту кривую пунктиром нанести реальную кривую для рабочего режима в условиях электрического пробоя межэлектродного пространства свечи зажигания, как показано на рис.4.

расчет магнитной цепи втягивающего электромагнита постоянного тока

Рассмотрим переходный процесс в катушке зажигания, имеющей индуктив­ность L и сопротивление R, после подклю­чения ее к источнику постоянного напряже­ния E (рис. 5). После коммутации ток в цепи будет увеличиваться от нуля до пре­дельного значения, равного установивше­муся постоянному току i_У=I=U/R. Энер­гия магнитного поля W_K катушки при этом также возрастет, и переходный процесс в рассматриваемой цепи будет связан с на­коплением энергии W_M=Lf²/2.

У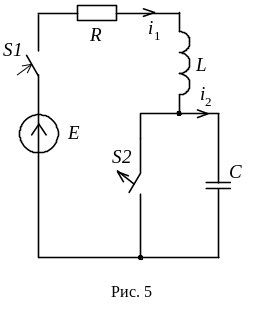 равнение электрического состояния цепи рис. 5 после замыка­ния выключателя S имеет вид

. (2.1)

Для свободного тока справедливо уравнение

с общим решением вида

,

где  = L/R — постоянная времени.

Переходный ток в цепи определяется суммой установившейся и свободной составляющих:

i_nep= i_У+ i_СВ = E/R + Ае^-t/. (2.2)

Для определения постоянной интегрирования А воспользуемся первым законом коммутации. До замыкания выключателя ток в ин­дуктивной катушке был равен нулю, следовательно, в первый момент после замыкания выключателя ток будет также равен нулю:

i₍₀₊₎= i_(0–) = U/R + А = 0.

Отсюда A = – E/R, поэтому выражение (2.2) можно представить в виде

,

т. е. ток в цепи нарастает до установившегося значения U/R по экспоненци­альному закону с постоянной времени  =L/R. Чем меньше со­противление R, тем больше предельное значение тока в цепи и тем больше энергия, которая будет накоплена в магнитном поле катушки.

При подключении к источнику постоянного напряжения E индук­тивной катушки, схема замещения которой состоит из последователь­но соединенных резистивного и индуктивного элементов (см. рис. 5), напряжения на этих элементах изменяются следующим образом. На­пряжение на резистивном элементе с сопротивлением R пропорцио­нально току:

u_R = Ri = U(1– e^-t/).

Напряжение на индуктивном элементе с индуктивностью L

График изменения напряжения на резистивном и индуктивном эле­ментах приведен на рис. 6. В первый момент времени после под­ключения источника напряжение на индуктивном элементе скачком возрастает до значения u_L = U, после чего по экспоненциальному за­кону уменьшается до нуля.

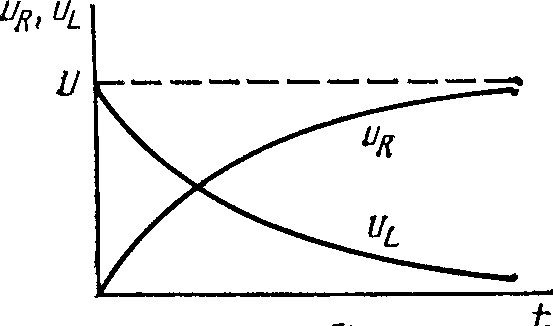
Рис.6

При размыкании ключей в электрических цепях, содержащих катушки с большой индуктивностью, на отдельных участках могут возникать наряжения, во много раз превышающие установившиеся. До размыкания ключа через индуктивность протекает ток. В катушке индуктивности была запасена энергия Li2/2Если размыкание ключа произошло мгновенно и дуга не возникла, то ток после коммутации в первый момент не изменится и за счет запаса магнитной энергии будет протекать по замкнутому контуру. При этом на концах обмотки возникнет пиковое напряжение , которое определяется как UC (0+) = R₁I₀ = nU₀. За время t = 4 RC.