
- •Федеральное агентство по образованию
- •Часть 1. Неопределённый интеграл
- •Пример решения простейшего интеграла.
- •На будущее:
- •Наиболее популярные методы решения неопределённых интегралов
- •1. Замена переменной интегрирования.
- •2. Приведение к «табличному виду».
- •3. Замена функции.
- •4. Интегрирование «по частям»
- •Рациональные дроби
- •Метод «неопределённых коэффициентов»
- •6. Тригонометрические функции.
- •6.1. Интегралы типа , .
- •6.2. Интегралы типа
- •6.3. Интегралы типа
- •6.4. Интегралы типа
- •6.5. Интегралы типа .
- •2А: ─ см. Пример 3;
- •2Б: ─ см. Пример 9.
- •7. Тригонометрические подстановки
- •8. Интегралы с иррациональностью типа .
- •Приложение 2 Построение таблицы исходных данных и соответствующего ей совмещённого графика
- •Построение графика
- •Часть I. Неопределённый интеграл Кузема Владимир Евгеньевич Требухин Сергей Александрович
- •620002, Екатеринбург, ул. Мира,19
- •620002, Екатеринбург, ул.Мира,19
Приложение 2 Построение таблицы исходных данных и соответствующего ей совмещённого графика
Для понимания предлагаемого алгоритма необходимы всего лишь минимальные навыки работы в Microsoft Excel любой версии.
Рассмотрим этот
алгоритм на примере задачи-образца.
Напомним, что в этой задаче решался
интеграл
=![]() ,
и было получено решение
=
+С.
Поэтому будем исследовать поведение
подынтегральной функции
,
и было получено решение
=
+С.
Поэтому будем исследовать поведение
подынтегральной функции
![]()
![]() и первообразной функции
и первообразной функции
![]() +С
в диапазоне значений аргумента
.
+С
в диапазоне значений аргумента
.
Для создания графика функции необходимо сначала оформить таблицу базовых данных (Таблица П1), содержащую:
начальное значение аргумента хнач;
конечное значение аргумента хкон;
шаг изменения аргумента ∆x, рассчитанный на определённое количество точек графиков (здесь в качестве взято число, равное 10);
константу интегрирования , значение которой подбирается из соображений усиления наглядности рисунка.
Например, такая таблица для нашего примера может иметь следующий вид:
Таблица П1. Базовые данные для построения таблицы исходных данных.
-
хнач
хкон
x
C
0
1,5708
0,15708
-1
В данном случае
эта таблица расположилась в диапазоне
ячеек
![]()
Затем строим таблицу исходных данных:
в любую свободную ячейку, например,
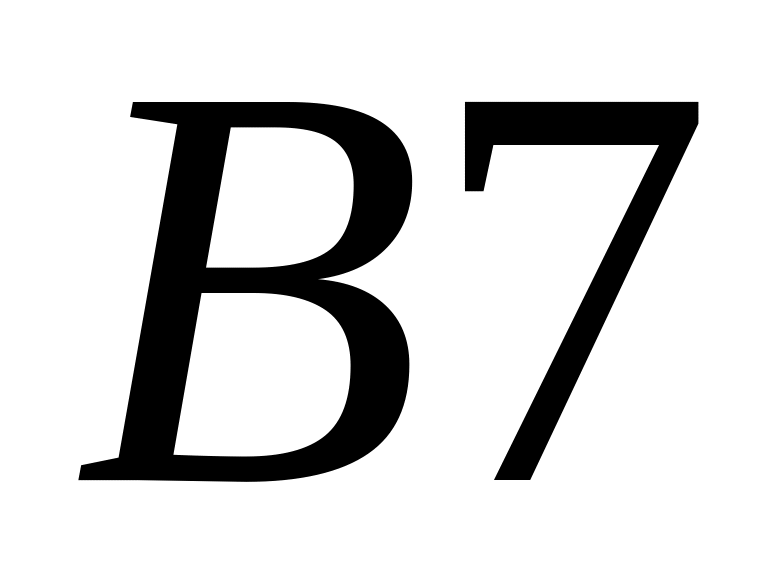 вписываем текст
вписываем текст
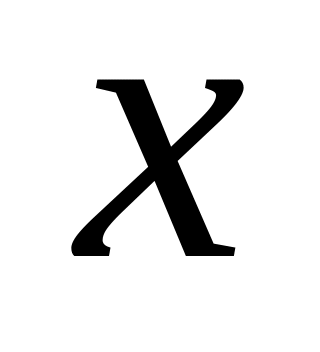 ,
левее в ячейку
,
левее в ячейку
 ,
─ текст
и, наконец, в ячейку
,
─ текст
и, наконец, в ячейку
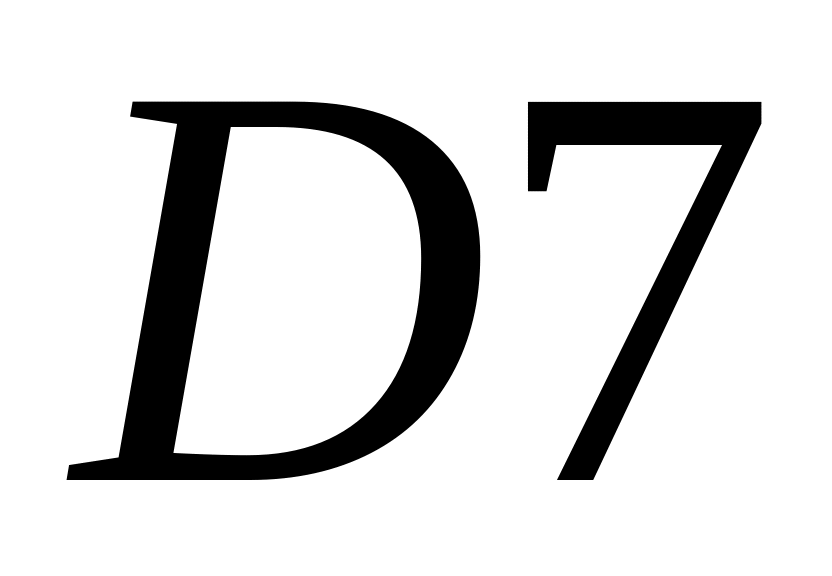 - текст
.
Таким образом, мы оформили «шапку»
таблицы;
- текст
.
Таким образом, мы оформили «шапку»
таблицы;формируем столбец , представляющий собой арифметическую прогрессию, первый член которой соответствует хнач, а разность - ∆x. Для этого в ячейку
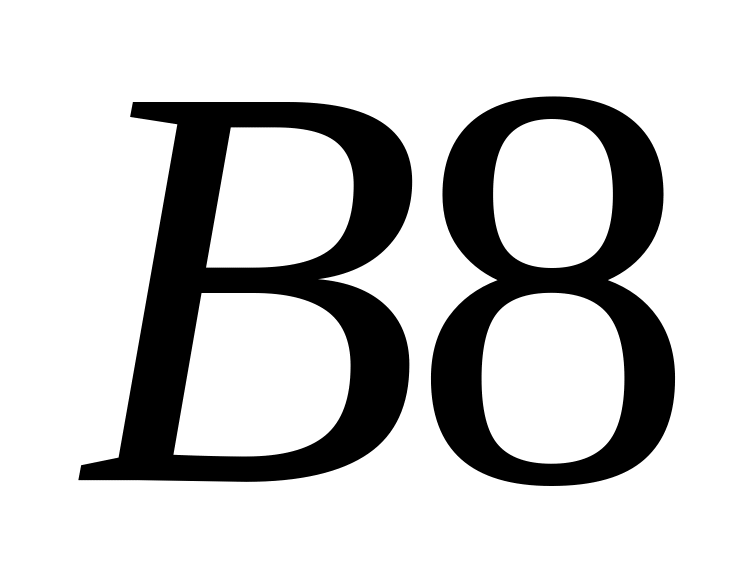 вводим формулу:
вводим формулу:
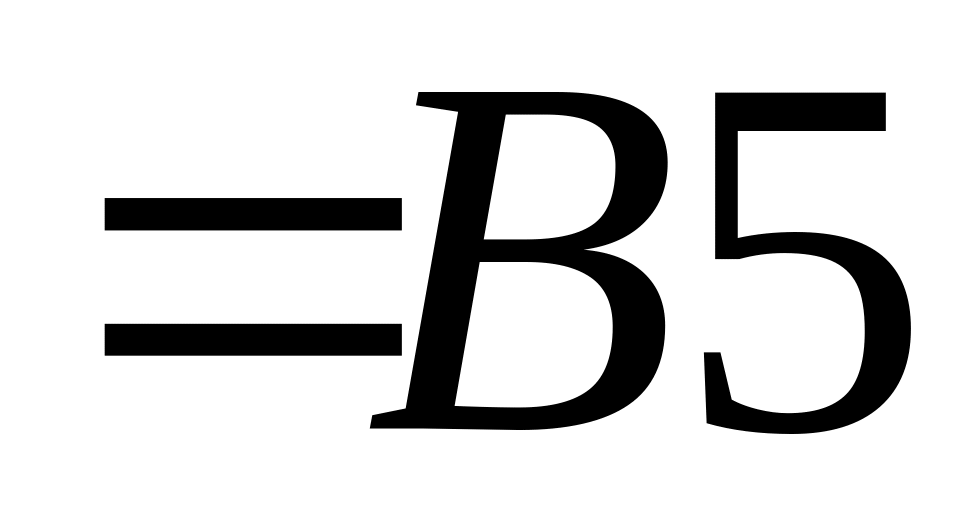 ,
а в ячейку
,
а в ячейку
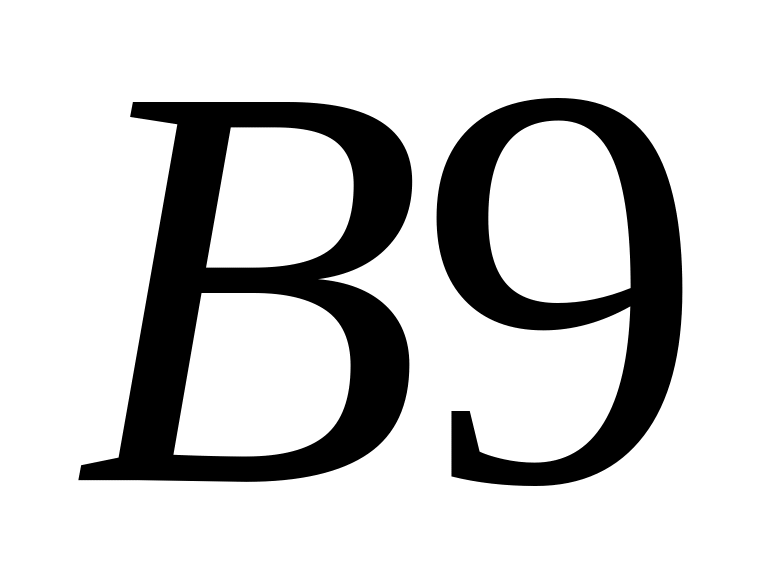 другую формулу:
другую формулу:
 +$
$
+$
$ (значки $ фиксируют адрес приращения
аргумента). Затем перемещаем курсор в
нижний правый уголок ячейки
до появления чёрного крестика, фиксируем
левую кнопку мышки и «протягиваем» эту
ячейку до конца таблицы;
(значки $ фиксируют адрес приращения
аргумента). Затем перемещаем курсор в
нижний правый уголок ячейки
до появления чёрного крестика, фиксируем
левую кнопку мышки и «протягиваем» эту
ячейку до конца таблицы;переходим к формированию столбца . Для этого в ячейку
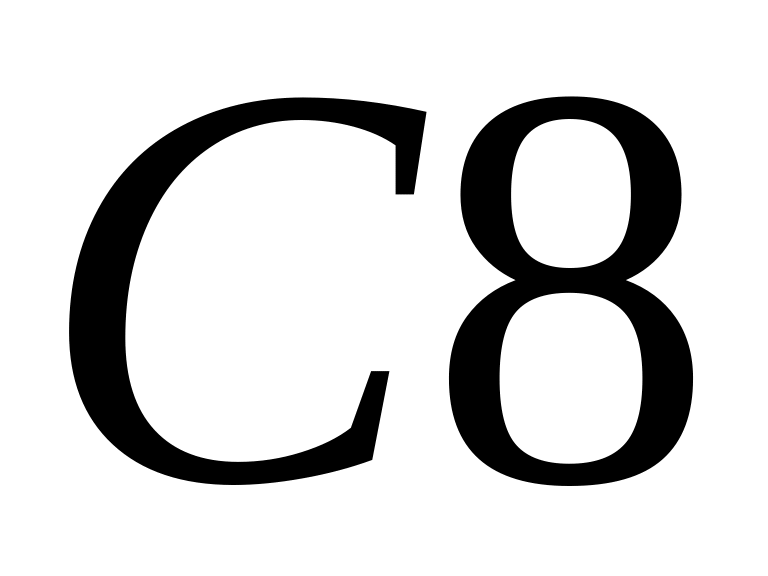 вводим соответствующую формулу со
ссылками на функции
вводим соответствующую формулу со
ссылками на функции
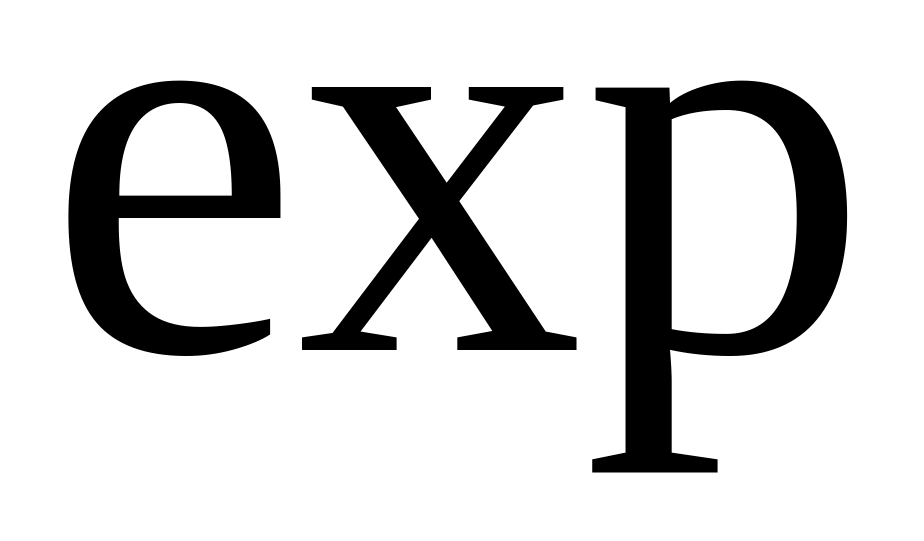 и
и
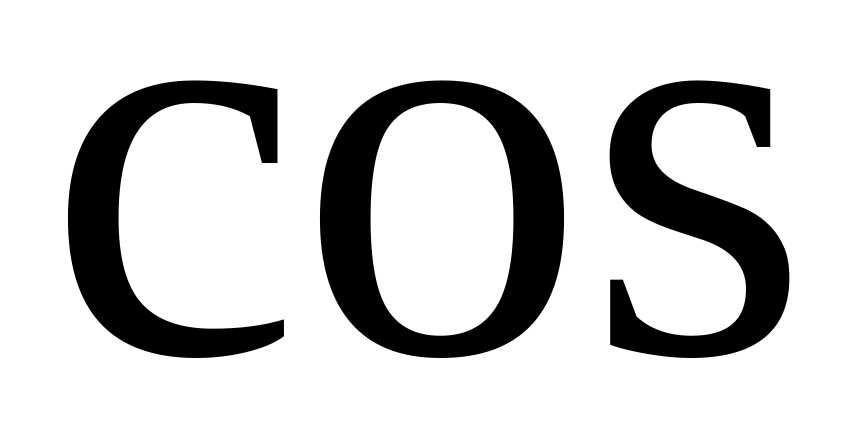 ,
которые, в свою очередь ссылаются на
ячейку
в качестве аргумента;
,
которые, в свою очередь ссылаются на
ячейку
в качестве аргумента;аналогично формируется столбец , начиная с ячейки
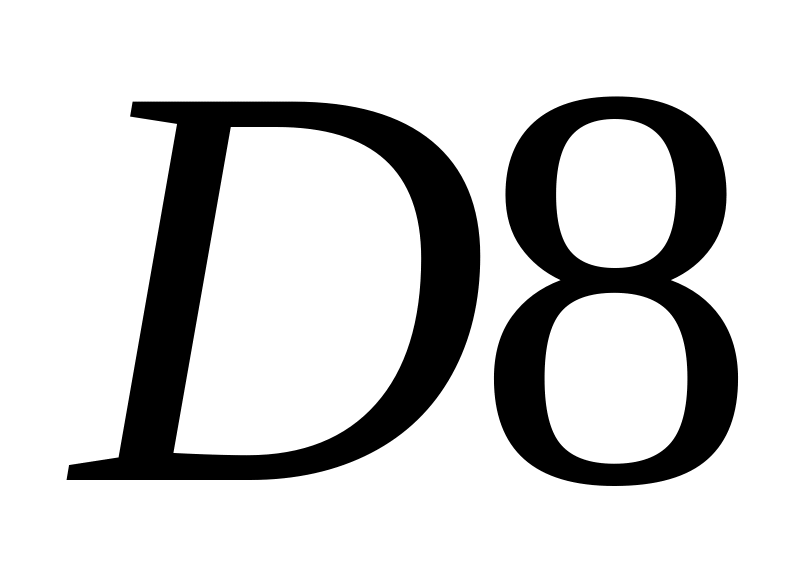 с использованием ещё одной функции
с использованием ещё одной функции
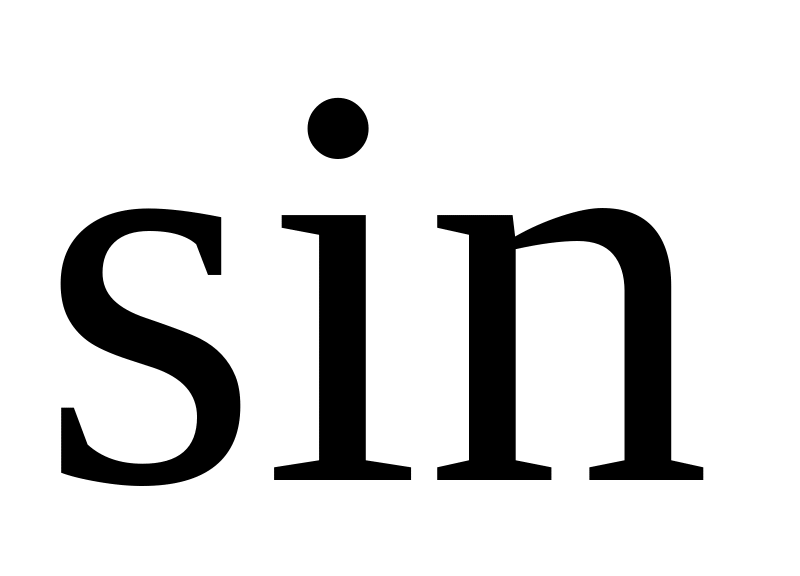 ;
;затем выделяем ячейки и в качестве диапазона ячеек, перемещаем курсор в правый нижний угол ячейки и аналогично действиям предыдущего пункта «протягиваем» обе ячейки до конца таблицы.
Теперь черновой вариант таблицы сформирован, осталось только произвести «косметические» правки: выравнивание «по центру», оформление бордюра и т.д.
-
x
f(x)
F(x)
0
-7,00
-0,65
0,16
-1,15
-1,30
0,31
1,61
-1,20
0,47
0,86
-0,98
0,63
-0,18
-0,94
0,79
-0,30
-0,98
0,94
-0,05
-1,01
1,10
0,07
-1,01
1,26
0,04
-1,00
1,41
-0,01
-1,00
1,57
-0,01
-1,00
Табл. П2.Таблица исходных данных для пос-
троения совмещённых графиков подынтег-
ральной и первообразной функций
Для распечатки этой таблицы необходимо:
выделить таблицу П2;
в панели «Меню» зайти в пункт «Файл»;
в появившемся вертикальном меню щёлкнуть по пункту «Печать»;
затем в одноимённом Диалоговом Окне щелкнуть в окошечке «Выделенный диапазон»;
и, наконец, щёлкнуть по кнопке
 .
.
Отпечатанную таблицу вырезать и приклеить в нужном месте отчёта.
