1.3 Охарактеризувати витрати напору при рівномірному русі рідини
Равномерное движение жидкости возможно лишь при отсутствии местных сопротивлений. Следовательно, в этом случае существуют только линейные потери напора.
С целью получения общего выражения для этих потерь составим динамическое уравнение равномерного движения потока жидкости.
Предположим, имеется поток жидкости с равномерным движением, ось которого наклонена к горизонту под углом . Выделим в этом потоке двумя живыми сечениями 1 и 2 объём малой длины L и применим к его движению теорему теоретической механики о движении центра масс. Так как движение жидкости равномерное, то ускорение центра масс выделенного объёма равняется нулю. Отсюда следует, что сумма проекций всех внешних сил, приложенных к указанному объёму, на любую ось также должна равняться нулю.
Такими внешними силами являются:
Силы давления
и
в сечениях 1 и 2, нормальные к этим
сечениям и направлены: первая – в
сторону движения, вторая – в сторону,
обратную движению; эти силы равны
произведению средних гидродинамических
давленийв этих сечениях на величину
площади сечения потока:
Силы давления на боковую грань рассматриваемого объёма жидкости со стороны ограничивающего его стенок
,
направленные нормально к этой поверхности;Сила тяжести, направленная по вертикали вниз, определяемая выражением
;Сила сопротивления движению Т.
Сделаем допущение,
что все частицы жидкости движутся с
одинаковыми скоростями, равными средней
скорости потока. Тогда сила сопротивления
будет равняться силе трения, возникающей
на боковой поверхности выделенного
объёма. Дляеё нахождения обозначим силу
трения, приходящуюся на единицу
поверхности через
.
Где А – смоченный периметр.
Составим сумму проекций:
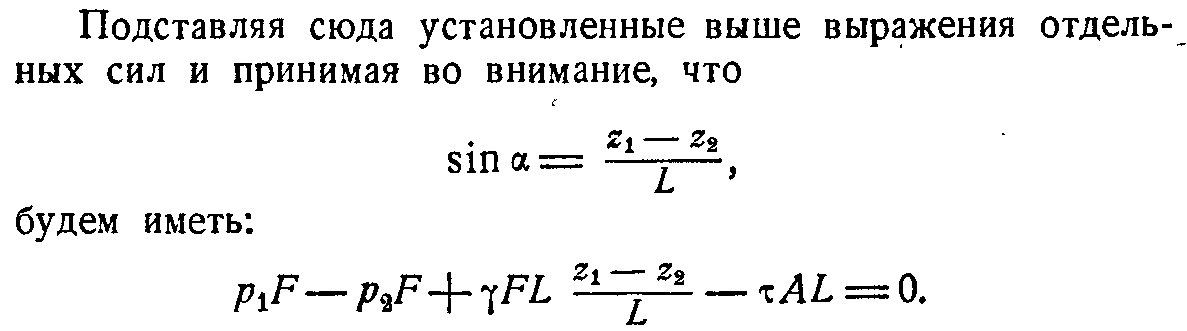
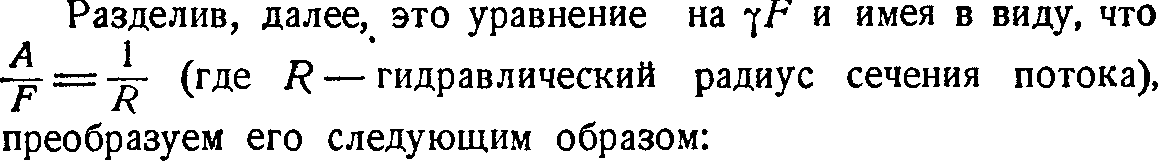
Сравнивая полученное уравнение с уравнением Бернулли, выражение для потер напора будет иметь вид:
2. Задачі
2.1. Визначити силу тиску на вільну поверхню в закритій посудині, якщо рівень рідини у відкритому п’єзометрі вище рівня рідини в посудині на h=2,3 м, а атмосферний тиск рівняється pатм.=1010 ГПа. Густина рідини рівняється ρ=700 кг/м3 .
Давление на свободной поверхности трубки равняется давлению в сечении А пьезометра и определяется по основному уравнению гидростатики:
Удельный
вес воды
Р = 1 + 0,0007 ∙ 230=1,161(кг/см2)
2.2. Із отвору у боковій стінці посудини по горизонтальній трубі змінного перерізу витікає вода. Визначити витрати води Q, а також середню швидкість і тиск в перерізах трубопроводу 1,2 і 3, рівень рідини в посудині вважати постійним і не враховувати гідравлічний тиск при наступних даних: висота Н=2 м, d1=7,5 см, d2=25 см, d3=10 см.
Составим уравнение Бернулли для двух сечений: сечения свободной поверхности жидкости в сосуде а-а и выходного сечения трубы 3,принимая за плоскость сравнения горизонтальную плоскость,проходящую через ось трубопровода. Имеем:
Ввиду значительных размеров сосуда по сравнению с поперечными размерами трубопровода скорость будет весьма мала и ею можно пренебречь. Учтём также,что (атмосферное давление).
Тогда получаем:
Отсюда находим:
и
Далее, по уравнению расхода определяем средние скорости в сечениях 1 и 2:
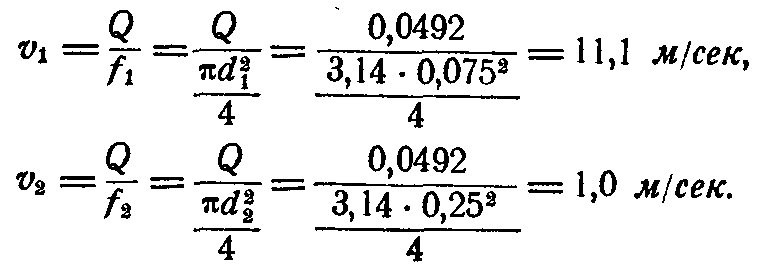
Затем по уравнению Бернулли, составляемому для сечений 1 и 3 и сечений 2 и 3,находим давления в сечениях 1 и 2; имеем:
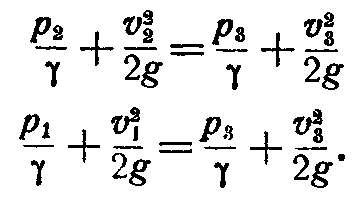
Отсюда получаем:
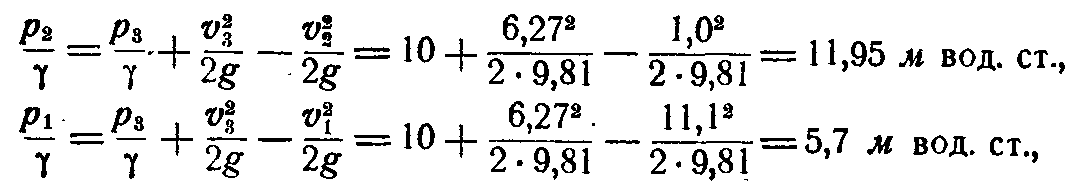
что соответствует
Таким образом, в сечении 1 имеет место вакуум(разрежение).