1.4.1.3. Ограниченные множества вещественных чисел

Рассмотрим произвольное множество вещественных чисел, которое будем обозначать символом x. Будем предполагать, что множество x содержит хотя бы одно число (непустое множество). Обозначение: x.

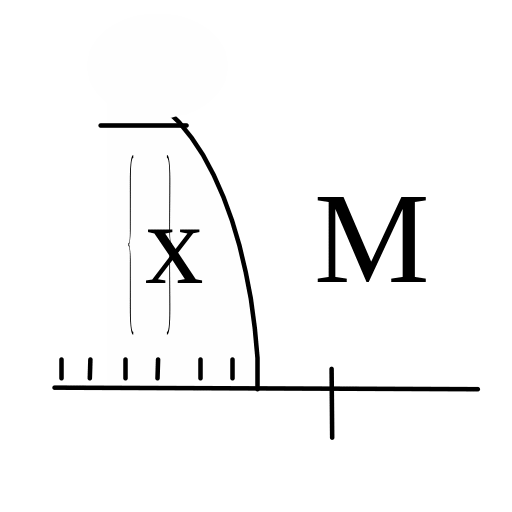
Определение 1. Множество вещественных чисел x называется ограниченным сверху (снизу), если существует такое вещественное число М (число m), что каждый элемент x множества удовлетворяет неравенству

x  М. (x  m).

Класс ограниченных сверху (снизу) множеств вещественных чисел будем обозначать символом , так что запись означает, что множество вещественных чисел x является ограниченным сверху (снизу).

На языке алгебры логики данные определения формулируются следующим образом:

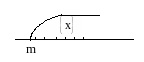
Числа М и m называются, соответственно, верхней гранью (нижней гранью) множества x.

Замечание. Если вещественное число М является верхней гранью множества x, то и любое вещественное число М¹, большее М, также является верхней гранью этого множества. Отсюда вытекает, что любое ограниченное сверху множество x имеет бесконечно много верхних граней.

Аналогичные выводы можно сделать и в отношении нижних граней ограниченного снизу множества x.

Пример 1. Множество всех целых отрицательных чисел

-1,-2,-3,... ограничено сверху. В качестве верхней грани этого множества можно взять любое вещественное число М, удовлетворяющее неравенству М-1.

Пример 2. Множество всех положительных вещественных чисел ограничено снизу. В качестве нижней грани этого множества можно взять любое неположительное вещественное число.

Определение 2. Точной верхней гранью ограниченного сверху множества x называется наименьшая из всех верхних граней этого множества. Точная верхняя грань x обозначается символом (sup - первые три буквы латинского слова supremum (“супремум”), которое переводится как “наивысшее”).

Наибольшая из всех нижних граней ограниченного снизу множества x называется точной нижней гранью этого множества и обозначается символом (от латинского слова infimum (“инфимум”), которое переводится как “наинизшее”).

Определение 2 формулируют чаще и по-другому:

Число (число ) называется точной верхней (точной нижней) гранью ограниченного сверху (снизу) множества x, если выполнены следующие два требования:

1) каждый элемент xx удовлетворяет неравенству ;

2) каково бы ни было вещественное число x¹ меньшее (большее ), найдется хотя бы один элемент , удовлетворяющий неравенству .

В этом определении требование 1 означает, что число (число ) является одной из верхних (нижних) граней, а требование 2 показывает, что эта грань является наименьшей (наибольшей) и уменьшена (увеличена) быть не может.

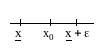
Пример 3. У множества всех целых отрицательных чисел -1,-2,-3,... существует точная верхняя грань x= -1, которая принадлежит этому множеству (т.е. является наименьшим элементом этого множества).

У множества всех положительных вещественных чисел существует точная нижняя грань- число 0, причем это число не принадлежит указанному множеству.

Имеет место следующая теорема.

Теорема 1.

(x) .

Если множество вещественных чисел содержит хотя бы один элемент и ограничено сверху (снизу), то существует вещественное число , которое является точной верхней (точной нижней) гранью этого множества.

Доказательство данной теоремы можно найти в некоторых работах.¹