1.4.3.12. Предельный переход в функциональных неравенствах

Пусть функции f(x), g(x), h(x) заданы в проколотой - окрестности т. а .

Теорема 1.

(рис.6)

Пусть функция f(x) имеет в т. а предел, равный b. Если в указанной окрестности точки а (за исключением, может быть, самой точки) выполняется неравенство f(x)c (f(x) c), где с - некоторая константа, то предел функции f(x) в т. а удовлетворяет неравенству bc (bc).

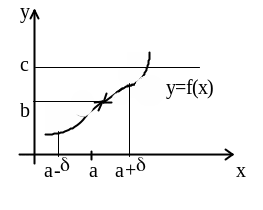
Рис. 6

Доказательство:

Пусть {x_n}- какая-нибудь последовательность Гейне, тогда по определению предела (по Гейне) функции f(x) в т. а : , причем f(x_n)c. По теореме о предельном переходе для последовательностей Но , поэтому bс. Для случая f(x) c доказательство аналогично.

Следствие 1.

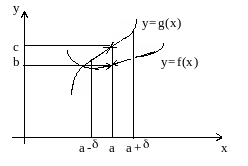
Рис. 7

Следствие 2.

Рис. 8

Теорема 2.

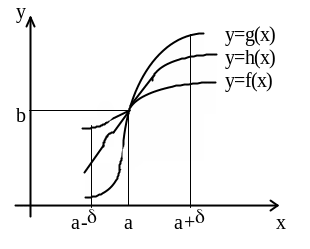
Рис.9

Доказательство: В отличие от предыдущих утверждений, здесь нужно доказать существование предела h(x) при xа. Пусть {x_n}- произвольная последовательность Гейне. Тогда и, кроме того, f(x_n)h(x_n)g(x_n). По теореме 2 п. 2.9 для последовательностей существует . Так как последовательность {x_n}- произвольная последовательность Гейне и , то по определению предела (по Гейне) существует . Терема доказана.

1.4.3.13. Определение непрерывности функции в точке и на множестве

Пусть {x} - область определения функции f(x), а{x} и любая - окрестность т. а содержит точки {x}, отличные от а.

Определение 1. Функция f(x) называется непрерывной в т. а, если

(Обозначение : f(x)С{a}).

Определение 2.

Определение 3.

.

Замечание 1. В определении 2 нет условия x_n а, в 3 - нет условия

x-a>0. Эти определения (2 и 3) эквивалентны.

Определение 4. Функция f(x) непрерывна в т. а слева, если

Определение 5. Функция f(x) непрерывна в т. а справа, если

Замечание 2. Если функция непрерывна в т. а справа и слева, то она непрерывна в т. а. Это следует из замечания п.1.4.3.8.

Определение 6. Точки, в которых функция f(x) не обладает свойством непрерывности, называются точками разрыва этой функции.

Пример 1. f(x)=xⁿ (nN) непрерывна в т. а (аR).

.

Пример 2.

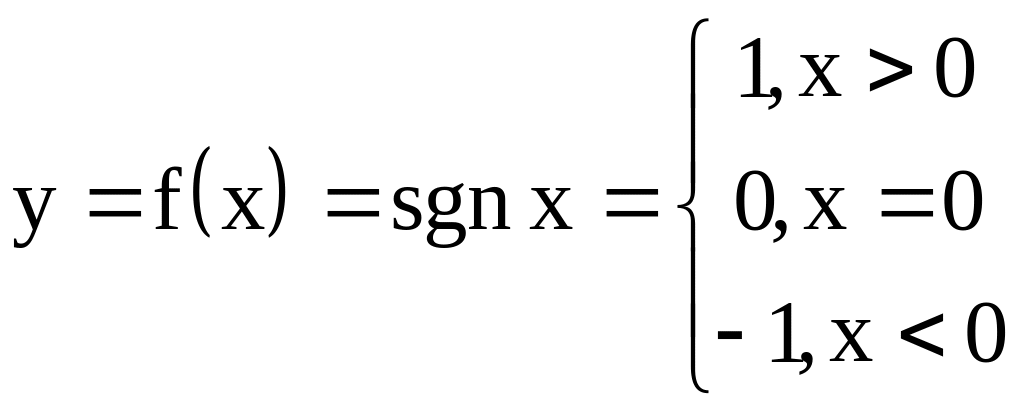разрывна в т. x=0,

не существует y=sgnx разрывна в т. x=0. В остальных точках она непрерывна.

Пример 3. Функция Дирихле y=D(x) разрывна в каждой точке, т.к. нет предела в каждой точке. (Докажите это, построив последовательность рациональных и последовательность иррациональных чисел, сходящихся к этой точке).

Определение 7. Функция f(x) непрерывна на множестве М(f(x)C(М)), если она непрерывна в каждой точке множества М.

Определение 8. Функция f(x) называется непрерывной на сегменте [a,b], если она непрерывна в каждой внутренней точке этого сегмента и, кроме того, непрерывна справа в т. а и непрерывна слева в b (f(x) C[a,b]); (для интервала f(x) C(a,b)).

1.4.3.14. Арифметические действия над непрерывными функциями

Теорема. Пусть f(x) и g(x) заданы на множестве {x}. Если эти функции непрерывны в т. x=а, то функции f(x)  g(x), f(x)g(x), непрерывны в точке x=а (частное при условии g(a))

Доказательство:

По теореме о пределе разности, суммы, произведения и частного двух функций (теорема п.3.10)

(если g(а)). Эти равенства и означают непрерывность в т. а функций f(x)  g(x), f(x)g(x), .