Уравнение движения тела переменной массы

Выведем уравнение движения тела пе­ременной массы на примере движения ра­кеты. Если в момент времени t масса раке­ты т, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса систе­мы за отрезок времени dt

dp = [(m-dm) (v+dv)+dm (v + u)]- mv,

где и — скорость истечения газов относи­тельно ракеты. Тогда

dp = mdv + udm

(учли, что dm dv — малый высшего порядка малости по сравнению с осталь­ными).

Если на систему действуют внешние силы, то dp = Fdt, поэтому

Fdt = mdv + udm,

mdv/dt=F-udm/dt. (10.1)

Член -udm/dt называют реактивной силой F_p

Таким образом, мы получили уравнение движения тела переменной массы ma=F + F_p, (10.2)

Применим уравнение (10.1) к движе­нию ракеты, на которую не действуют ни­какие внешние силы. Полагая F = 0 и счи­тая, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим

т*dv/dt=-udm/dt. откуда

Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени скорость ра­кеты равна нулю, а ее стартовая масса то, то С = uln m₀. Следовательно,

v = uln(m₀/m). (10.3)

Это соотношение называется формулой Циолковского. Она показывает, что: 1) чем больше конечная масса ракеты т, тем больше должна быть стартовая масса ракеты то; 2) чем больше скорость истече­ния и газов, тем больше может быть ко­нечная масса при данной стартовой массе ракеты.

Работа, мощность

Работа силы — количественная характеристика процесса обмена энергией между взаимодействую­щими телами.

F_s =Fcos A = F_ss

В общем случае сила может изменять­ся как по модулю, так и по направлению, поэтому формулой пользоваться не­льзя. Если, однако, рассмотреть элемен­тарное перемещение dr, то силу F можно считать постоянной, а движение точки ее

приложения — прямолинейным. Элемен­тарной работой силы F на перемещении dr называется скалярная величина

dА =Fdr = Fcos•ds=F_sds,

где а — угол между векторами F и dr; ds = |dr| — элементарный путь; F_s — про­екция вектора F на вектор dr (рис. 13).

Работа силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных бесконечно малых участках пути. Эта сум­ма приводится к интегралу

Если, например, тело движется прямолинейно, сила F=const и =const, то получим

где s — пройденный телом путь (см. также формулу (11.1)).

Чтобы охарактеризовать скорость со­вершения работы, вводят понятие мощ­ности:

N=da/dt. = Fdr/dt=Fv

Кинетическая энергия механической системы — это энергия механического движения этой системы.

dA = dW = FVdt = dp/dt * Vdt = dp*v = p/m * dp;

W = int (0-p) pdp/m = mv^2/2;

Или сумма в случае системы мат точек.

Потенциальная энергия — механиче­ская энергия системы тел, определяемая их взаимным расположением и характе­ром сил взаимодействия между ними.

Пусть работа, совершаемая действующими сила­ми при перемещении тела из одного поло­жения в другое, не зависит от того, по какой траектории это перемещение прои­зошло, а зависит только от начального и конечного положений. Такие поля на­зываются потенциальными, а силы, дей­ствующие в них,— консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется диссипативной; ее примером является си­ла трения.

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией II. Работа консервативных сил при элемен­тарном (бесконечно малом) изменении конфигурации системы равна приращению потенциальной энергии, взятому со знаком минус, так как работа совершается за счет убыли потенциальной энергии:

dA = -dП. (12.2)

Работа dА выражается как скалярное произведение силы F на перемещение dr и выражение (12.2) можно записать в виде

Fdr=-dП. (12.3)

или в векторном виде

F=-gradП, (12.4) где

Для него наряду с обозначением grad П применяется также обозначение П.  («набла»)

Закон сохранения энергии

W= Wп+Wк При условии что внешние силы действующие на систему являются стационарными и потенциальными, а внутренние потенциальными, энергия

Wp+Wr = const.

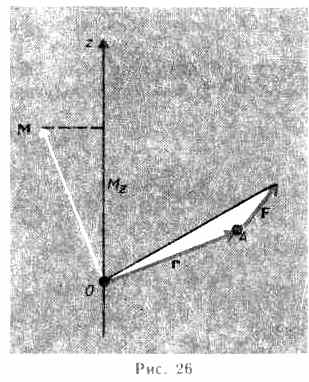
Момент инерции

Моментом инерции системы (тела) отно­сительно оси вращения называется физи­ческая величина, равная сумме произведе­ний масс n материальных точек системы на квадраты их расстояний до рассматри­ваемой оси:

В случае непрерывного распределения масс эта сумма сводится к интегралу

где интегрирование производится по всему объему тела. Величина r в этом случае есть функция положения точки с коорди­натами х, у, z.

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относи­тельно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела J относительно любой оси вращения равен моменту его инерции J_c относительно параллельной оси, про­ходящей через центр масс С тела, сло­женному с произведением массы m тела на квадрат расстояния а между осями: J = J_c + ma². (16.1)

Момент инерции цилиндра относительно его оси

Тонкостной цилиндр, r=R. J = int (m) r^2dm = R^2 * int (m) dm = m*R^2;

Сплошной цилиндр, r<=R, dJ = dm*r^2 = dm*(Ro)dV = (Ro)*2*pi*r*h*dr

J = int r^2dm = 2pi(Ro)h*int (0-R) r^2dr = 2pi(Ro)hR^4/4= mR^2/2

Момент инерции стержня относительно перпендикулярной оси

dJ=dm*r^2 = (Ro)Sr^2dr

dm=Sdr*(Ro)

J = 2*(Ro)*S * int (0-L/2) r^2dr = 2*(Ro)*S*r^3/3 | (0-L/2) = m*L^2/12 J = 2*(Ro)*S * int (0-L) r^2dr = *(Ro)*S*r^3/3 | (0-L) = m*L^2 /3

Кинетическая энергия вращения

Пусть есть объект m₁, m₂, ..., m_n, находящиеся на рас­стоянии r₁, r₂, ..., r_n от оси вращения. При вращении твердого тела относительно не­подвижной оси отдельные его элементар­ные объемы массами m_i, опишут окружно­сти различных радиусов r_i и имеют раз­личные линейные скорости v_i. Но так как мы рассматриваем абсолютно твердое те­ло, то угловая скорость вращения этих объемов одинакова:

 = v₁/r₁ = v₂/r₂ = ... = v_n/r_n. (17.1)

Кинетическую энергию вращающегося тела найдем как сумму кинетических энер­гий его элементарных объемов:

Используя выражение (17.1), получим

где J_z — момент инерции тела относитель­но оси 2. Таким образом, кинетическая энергия вращающегося тела

T_вр = J_z²/2. (17.2)