Работа N 1.1.

Исследование динамических характеристик типовых звеньев систем автоматического управления

2.1. Цель работы

Цель курсовой работы — изучить статические и динамические свойства элементарных и типовых звеньев, являющихся составными элементами сложных динамических систем автоматического управле­ния (объектов управления и регуляторов). Цель достигается путем получения аналитических выражений для временных и частотных ха­рактеристик, расчета и построения графиков указанных характери­стик, их анализа и обобщения.

Исходными данными для, выполнения курсовой работы являются дифференциальные уравнения (уравнения динамики) изучаемых звеньев. Эти уравнения приведены в приложении 9, а коэффициенты уравнений (в соответствии с номером варианта задания) — в прило­жениях 10, 11, 12, 13.

2.2. Содержание работы

1. Записать исходное дифференциальное уравнение в оператор­ной и стандартной форме, рассчитать для заданного варианта пара­метры звена (постоянные времени, коэффициенты передачи, декре­менты затухания).

2. Используя преобразования Лапласа, получить передаточную функцию звена, привести к стандартному виду и определить тип (на­звание) звена. Привести определение передаточной функции.

3. Привести определения временных характеристик звеньев и пол­учить аналитические выражения для переходной функции и функции веса.

4. Построить графики временных характеристик для данного ва­рианта исходных данных. Провести анализ характеристик, а именно,

выявить характерные особенности переходных процессов и влияние коэффициентов дифференциальных уравнений ( а_i, b_i, k_i, T_i, _i) на характеристики переходных процессов (переходной функции и функции веса).

5. Получить частотную (комплексную) передаточную функцию.

6. Привести определения частотных характеристик звеньев:

— амплитудной частотной характеристики (АЧХ);

— фазовой частотной характеристики (ФЧХ);

— амплитудно-фазовой частотной характеристики (АФЧХ);

— логарифмической амплитудной частотной характеристики (ЛАЧХ);

— логарифмической фазовой частотной характеристики (ЛФЧХ);

— логарифмической амплитудно-фазовой частотной характери­стики (ЛАФЧХ), и получить аналитические выражения для указанных характеристик.

7. Построить графики всех частотных характеристик и провести их анализ, охарактеризовать зависимость усиления амплитуды и сдви­га фазы от частоты и выявить влияние коэффициентов дифференци­альных уравнений ( а_i, b_i, k_i, T_i, _i) на частотные характеристики

звеньев.

Примечание. В заданиях 16...19 предлагается построить только асим­птотические ЛАЧХ и ЛФЧХ.

2.3. Методические указания к выполнению работы №1

1. Началу работы должно предшествовать изучение соответству­ющих тем теории автоматического управления, например, по учебни­кам [1, с. 76—124] или [2, с. 15—43).

2. Аналитические выражения для переходных характеристик можно получить решением дифференциальных уравнений, описываю­щих динамику звеньев. При этом можно воспользоваться как класси­ческим подходом (см. курс «Математический анализ»), так и оператор­ными методами, в частности преобразованиями Лапласа с последую­щим переходом к оригиналу, т.е. к функциям времени [1,с. 235-242]. Не следует забывать, что если найдена переходная функция, то фун­кцию веса можно получить дифференцированием переходной функ­ции.

П ример 1. Динамика звена описывается дифференциальным урав­нением:

Найти выражение для переходной функции и функции веса. Ис­ходное уравнение необходимо преобразовать к стандартному виду:

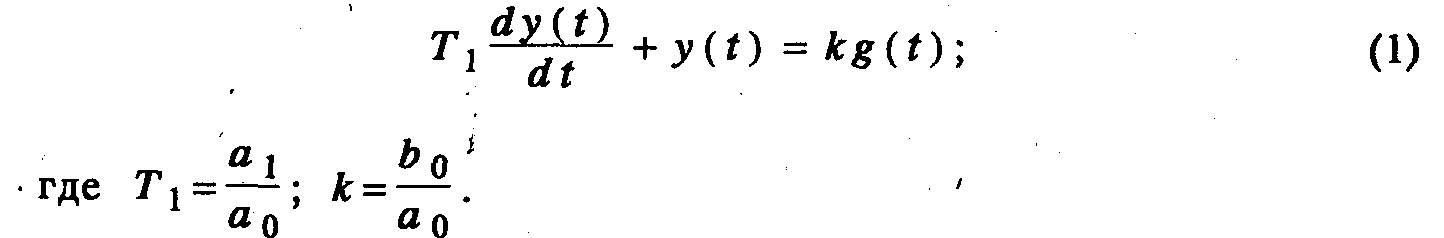
Решение уравнения (1) для определения переходной функции мо­жет быть записано как сумма решений однородного уравнения и час­тного решения при g(t)=l(t) при нулевых начальных условиях:

Подставив в (2) у(0)=0 при t=0, найдем, что C=-k1(t). Сле­довательно, переходная функция запишется в виде

Продифференцировав выражение (3), получим функцию веса:

Пример 2. Решить уравнение (1) с помощью преобразований Лапласа. Передаточная функция звена, заданного уравнением (1), имеет вид

а преобразования Лапласа входного сигнала l(t) имеет вид 1/s (приложение3).

Следовательно, преобразование Лапласа переходной функции

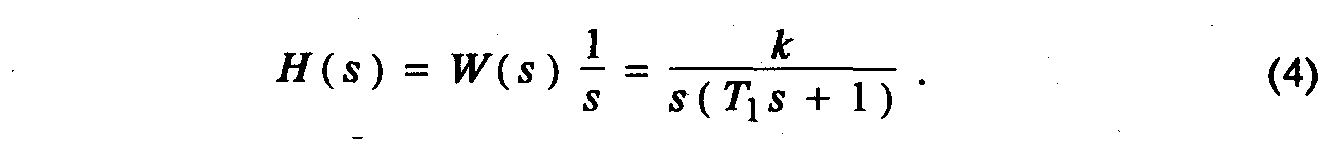
Разложив на элементарные дроби правую часть выражения (4), получим

и, переходя к оригиналу, окончательно запишем:

что, естественно, совпадает с уравнением (3).

Функция веса находится аналогично. Имеем L{(t)}=1. Тогда

Переходя к оригиналу, получим

Для большей наглядности при анализе динамических звеньев и систем целесообразно разместить временные графики один под другим и выполнить их в одинаковом масштабе по оси абсцисс (по оси времени).

3. Вывод частотной комплексной передаточной функции можно осуществить применением формулы Эйлера для представления гармонической функции в виде экспоненциальной функции [1, с. 82—84, или 2, с. 21—35].

4. Для получения аналитических выражений частотных характеристик необходимо уметь осуществлять элементарные действия с комплексными функциями, основными из которых являются:

выделение действительной и мнимой составляющих;

нахождение модуля и аргумента комплексного выражения. Если комплексная функция представляет собой дробь, то для выделения действительной и мнимой составляющих целесообразно освободиться от мнимых слагаемых в знаменателе путем умножения числителя и знаменателя на комплексное выражение, сопряженное знаменателю.

Пример 3. Имеем частотную (комплексную) передаточную функцию:

Необходимо выделить действительную и мнимую составляющие

этой функции. Знаменатель представим выражением (-Т²+j), а комплексно

сопряженное ему выражение будет (- Т²-j). Тогда

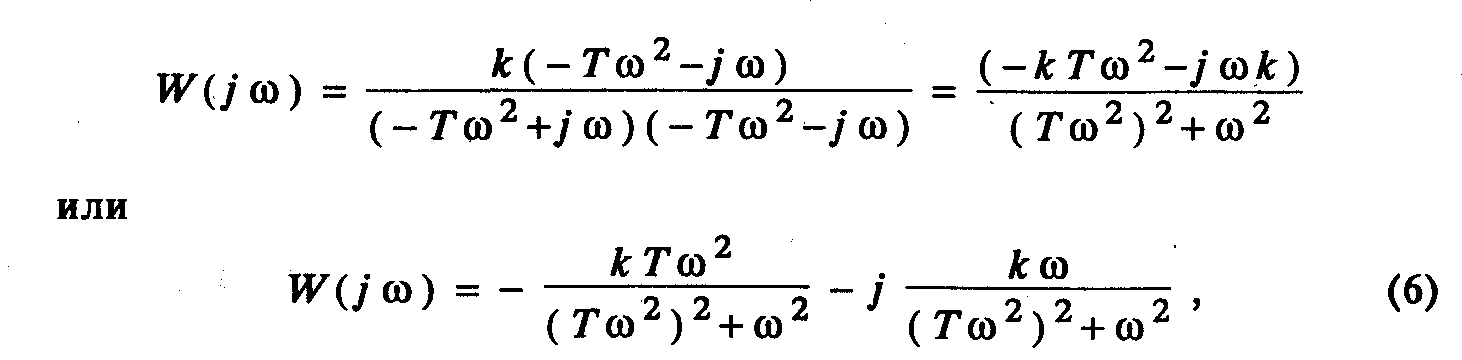
где первое слагаемое — действительная часть; второе — мнимая.

Модуль, частотной передаточной функции является амплитудно-частотной характеристикой звена или системы, а аргумент — фазовой частотной характеристикой. Согласно теории функций комплексного переменного модуль комплексного выражения равен корню квадрат­ному из суммы квадратов действительной и мнимой составляющих, а аргумент — арктангенсу отношения мнимой части к действительной, т.е.

где U() и V()— соответственно действительная и мнимая части комплексного выражения (б).

Пример 4. найти модуль и аргумент частотной передаточной фун­кции (5). Из выражения (6) следует, что

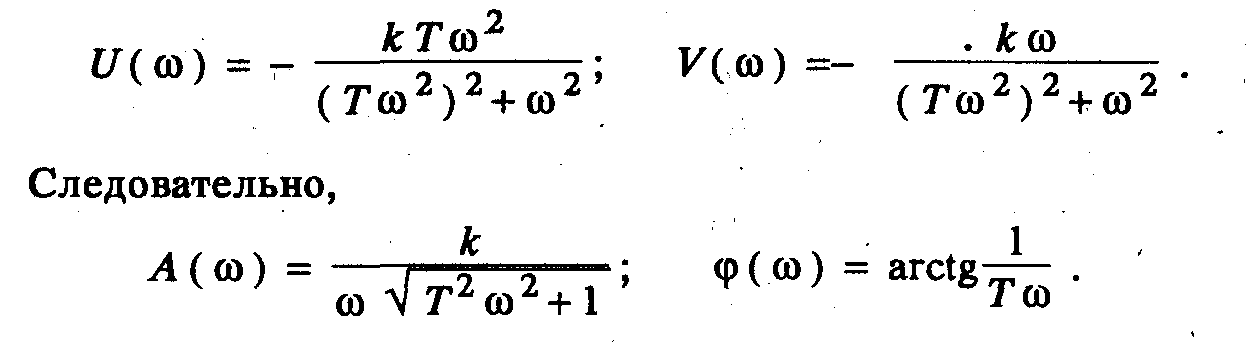
Однако во многих случаях модуль А() и аргумент f() проще находить, если вычислять раздельно модули и аргументы числителя и знаменателя передаточной функции.

Пример 5. Найти модуль и аргумент частотной передаточной функции (5), используя указанный подход:

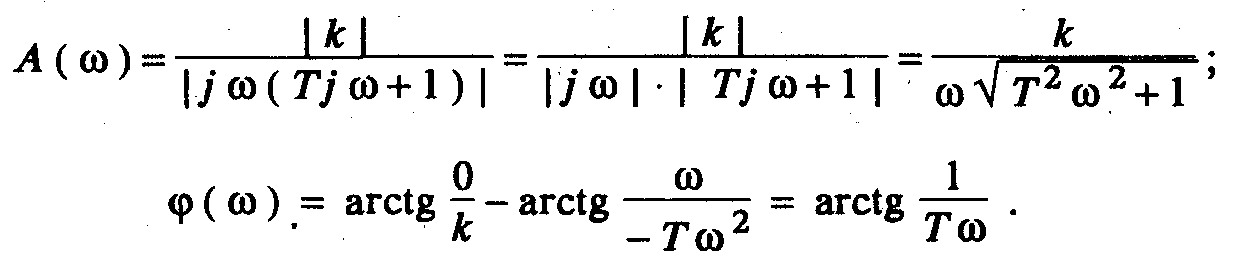
Результаты решения примеров 4 и 5 совпадают.

Если числитель и знаменатель передаточной функции представ­лены в виде произведений простых комплексных чисел, что часто име­ет место, то удобнее воспользоваться следующими правилами:

а) при умножении комплексных чисел их модули перемножаются, а аргументы складываются,

б) при делении — модуль числителя делят на модуль знаменате­ля, а из аргумента числителя вычитают аргумент знаменателя.

Пример 6. Найти модуль и аргумент частотной передаточной функции, заданной следующим образом:

Следуя правилам, приведенным выше, представим

5. При графическом построении амплитудно-фазовой частотной характеристики для наглядности целесообразно (где это возможно) использовать одинаковый масштаб по действительной и мнимой осям. При этом для расчетных точек на характеристике необходимо указать значения частоты со. В числе расчетных точек обязательно должны быть точки для значений частот: 0; 1/T; °°. На характеристике следует указывать направление возрастания значений частоты (стрелкой).

Амплитудно-частотную и фазовую частотную характеристики рекомендуется строить одну под другой с одинаковым масштабом по оси частот. Вертикальной пунктирной линией отмечают сопрягающие частоты (_c = 1/T или _c = 1/).

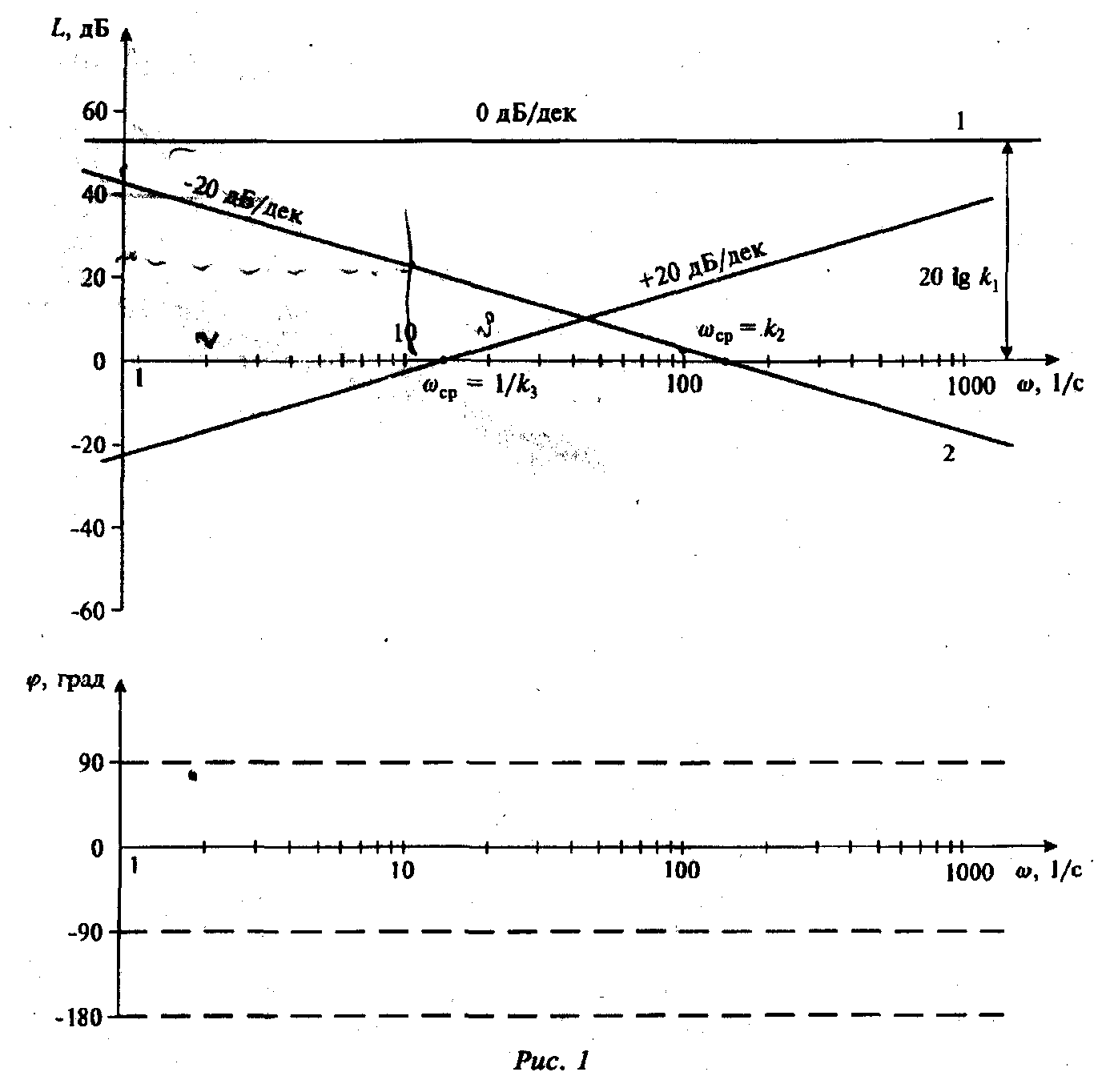
6. Для построения ЛАЧХ и ЛФЧХ используется стандартная сетка (рис. 1). По оси абсцисс откладывается угловая частота в логарифми­ческом масштабе и наносятся отметки, соответствующие lg со, а около отметок пишут значения частоты (О в рад/с. Увеличение частоты в 10 раз соответствует приращению логарифма на единицу, что составляет одну декаду.

Для построения этих характеристик целесообразно использовать специальную полулогарифмическую бумагу, однако можно использо­вать и обычную миллиметровую бумагу, но масштаб по оси частот должен быть логарифмическим. Логарифмический масштаб можно наносить с помощью логарифмической линейки. Однако это можно сделать и без логарифмической линейки. Для этого откладывают по оси частот требуемое количество декад (равных отрезков) и оцифро­вывают их значениями частот в зависимости от частотного диапазона, выбранного для исследования данного звена. Длину каждого отрезка, соответствующего одной декаде, принимают условно равной единице и разделяют метками со значениями 0,30; 0,48; 0,60 и т.д. от длины отрезка (рис. 2, нижняя шкала). Затем оцифровывают метки внутри декады, например, так, как оцифрована верхняя шкала на рис. 2 для случая изменения частоты от 10 до 100 рад/с.

При построении ЛАЧХ по оси ординат наносят равномерный мас­штаб и откладывают модуль А () в децибелах (-дБ):

Величина L() выражается в децибелах. Бел представляет собой логарифмическую единицу, соответствующую увеличению мощности в 10 раз, 2 Бела — в 100 раз, 3 Бела— в 1000 раз и т.д. Децибел равен одной десятой части Бела. Если бы A() было отношением мощностей, то перед логарифмом в правой части (9) должен бы стоять множитель 10. Но так как A() — это отношение выходной и входной величин (перемещений, скоростей, токов, напряжений и т.п.), а не мощностей, то увеличение этого отношения в 10 раз соответствует увеличению мощностей в 100 раз, что равняется двум Белам или двадцати децибелам. Поэтому в правой части (9) стоит множитель 20.

Один децибел характеризует изменение амплитуды в ²⁰10 1,12 раз.

Ось ординат может пересекаться с осью абсцисс при любом произвольном значении частоты О), так как точка w=0 на логарифмической оси лежит слева в бесконечности (lg0=-°°). Разумно ось ординат располагать так, чтобы справа от нее можно было показать весь характерный участок ЛАЧХ. Для этого ось ординат следует расположить левее самой малой сопрягающей частоты.

Фазовую характеристику рекомендуется располагать под амплитудной и строить в одинаковом масштабе по оси частот.

Преимуществом логарифмических частотных характеристик является возможность их построения практически без вычислительной работы, особенно это преимущество проявляется при построении асимптотических ЛАЧХ. Асимптотические ЛАЧХ представляют собой совокупность отрезков прямых линий с наклонами, кратными 20 дБ/дек. Ниже приведены примеры построения ЛАЧХ.

Пример 7. Модуль частотной передаточной функции имеет вид A() = k₁. Тогда L() = 20lg(k₁). Следовательно, ЛАЧХ представляет собой прямую, параллельную оси абсцисс, т.е. ее наклон равен нулю (прямая l на рис. 1).

Пример 8. Модуль частотной передаточной функции A() = lg(k₂/) = 20 lgk₂ – 20 lg.

Это прямая линия, пересекающая ось частот на частоте =k2 и имеющая отрицательный наклон 20 дБ/дек. Действительно, положив L() = 0, получим  = k₂. Наклон ( - 20 дБ/дек) объясняется тем, что увеличение частоты в 10 раз ( на одну декаду) приводит к уменьшению L(w) на 20 дБ (прямая 2 на рис. 1). Частоту, на которой ЛАЧХ пересекает ось абсцисс, называют частотой среза и обозначают wcp,.

Пример 9. Модуль частотной передаточной функции A(w)=k₃. Тогда L()=20lgk₃+20lg. Это прямая с положительным наклоном 20 дБ/дек (+20 дБ/дек), пересекающая ось абсцисс на частоте  = l/k₃ (прямая 3 на рис. 1).

Пример 10. Модуль частотной передаточной функции имеет вид

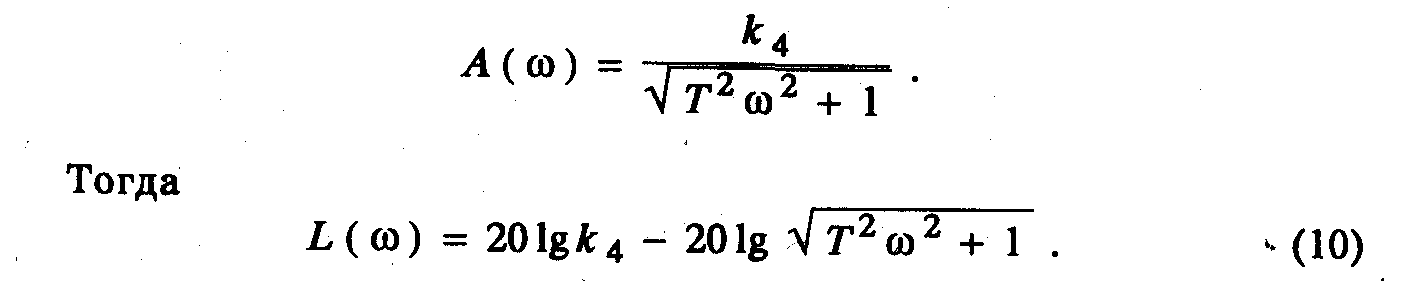
Построение ЛАЧХ показано на рис. 3. На стандартной сетке проводят вертикальную пунктирную прямую через точку с частотой  = 1/T, называемой сопрягающей частотой. Для частот со << 1/T — можно пренебречь первым слагаемым под корнем в выражении (10) и тогда левее сопрягающей частоты получим L(w)=201gk4, чему соответст­вует

вует прямая линия а-b, параллельная оси частот и являющаяся первой асимптотой. Для частот  >> 1/T в выражении (10) можно пренебречь вторым слагаемым под корнем и тогда будем иметь приближенное значение L(),=20lgk₄-20lgT, которому, согласно примеру 8, будет соответствовать прямая b-с с отрицательным наклоном 20 дБ/дек, являющаяся второй асимптотой. Ломаную линию a-b-с называют асимптотической ЛАЧХ, которая на самом деле несколько отличается от истиной ЛАЧХ (действительная ЛАЧХ показана пунктиром). Наибольшее отклонение будет в точке b, оно равно приближенно 3 дБ. Действительно асимптотическая ЛАЧХ в этой точке равна 201gk₄, а реальная L(w) = L(1/T) = 20 lg(k₄/v2) = 20lgk₄ - 3 дБ. Левее и правее сопрягающей частоты отличие от истинной ЛАЧХ будет меньше 3 дБ.

Пример 11. Модуль частотной передаточной функции А() = k₅²²+1.

Рассуждая как в примере 10, нетрудно увидеть, что асимптотическая ЛАЧХ представляет собой ломаную линию q-1-m (рис. 3). Первой асимптотой является прямая q-l с нулевым наклоном, а второй — прямая 1-т с положительным наклоном 20 дБ/дек. Асим­птоты стыкуются на сопрягающей частоте =1/т. Для апериодиче­ских и форсирующих звеньев первого порядка допустимо построение асимптотических ЛФЧХ. На рис. 4 в качестве примера приведены асимптотическая ЛФЧХ для апериодического звена первого порядка (ломаная а-b-c-d) и реальная ЛФЧХ (пунктиром). Видно, что они отличаются друг от друга не более чем на 5—6° максимально, а в не­которых точках, в том числе и на  = 1/T , совпадают в точности.

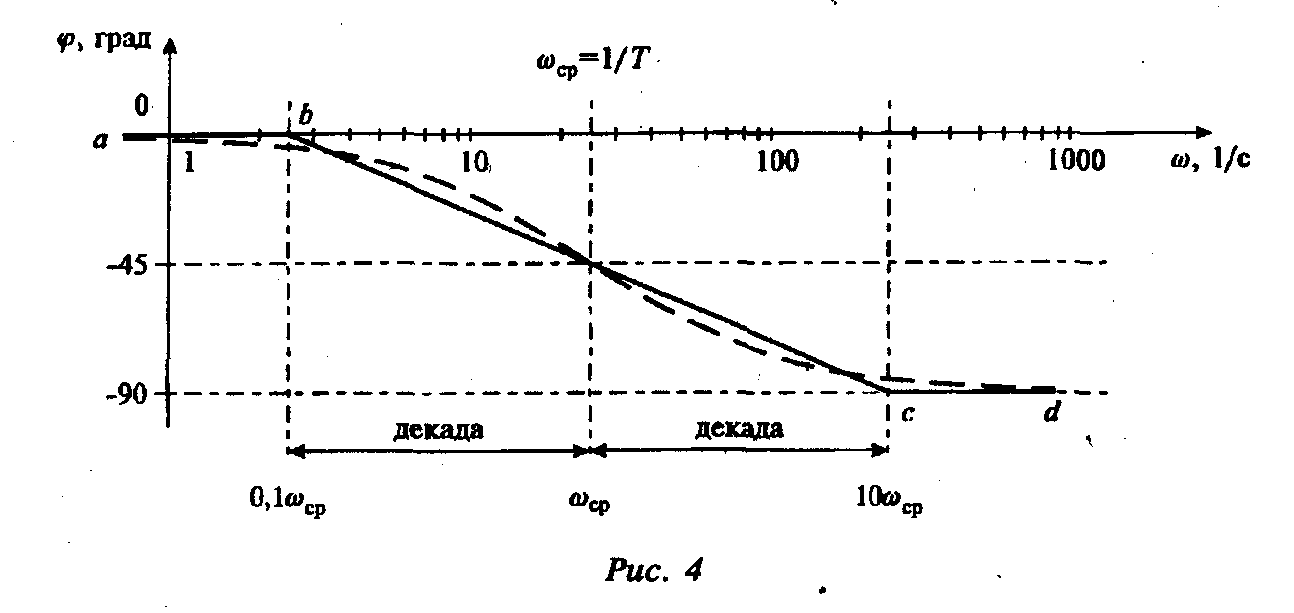
Для построения такой ЛФЧХ отмечают сопрягающую частоту ω = 1/T или ω = 1/t и значения частот, отстоящих от сопрягающей слева и справа на одну декаду

(0,1ω и 10ω). Затем на частоте 10ω откладывают значение фазового сдвига для апериодического звена первого порядка - 90° (для форсирующего звена + 90° ) и проводят прямую по оси частот слева до точки 0,1 со (отрезок а-b), потом прямую b-с до значения -90° на частоте 10ω и, наконец, прямую c-d правее 10w. При этом прямая b-с должна пройти через значение φ = -45° на частоте (ω = 1/T (или (φ = + 45° , на частоте ω = 1/τ ).

Для колебательных звеньев и форсирующих звеньев второго порядка такое построение ЛФЧХ невозможно, так как вид ЛФЧХ этих звеньев существенно зависит от численного значения декремента затухания ξ. Апериодическое звено 2-го порядка может быть представлено в виде произведения двух апериодических звеньев 1-го порядка. В этом случае можно по указанному принципу построить ЛФЧХ для каждого звена отдельно и путем их сложения получить результирующую ЛФЧХ.

7. При выполнении работы можно воспользоваться следующими рекомендациями.

Выражения для всех временных и частотных характеристик целесообразно получить в общем виде, а конкретные исходные данные подставить только при конечных расчетах.

Все результаты расчетов для построения временных и частотных характеристик удобно свести в таблицы. Например, для временных характеристик таблица может иметь вид

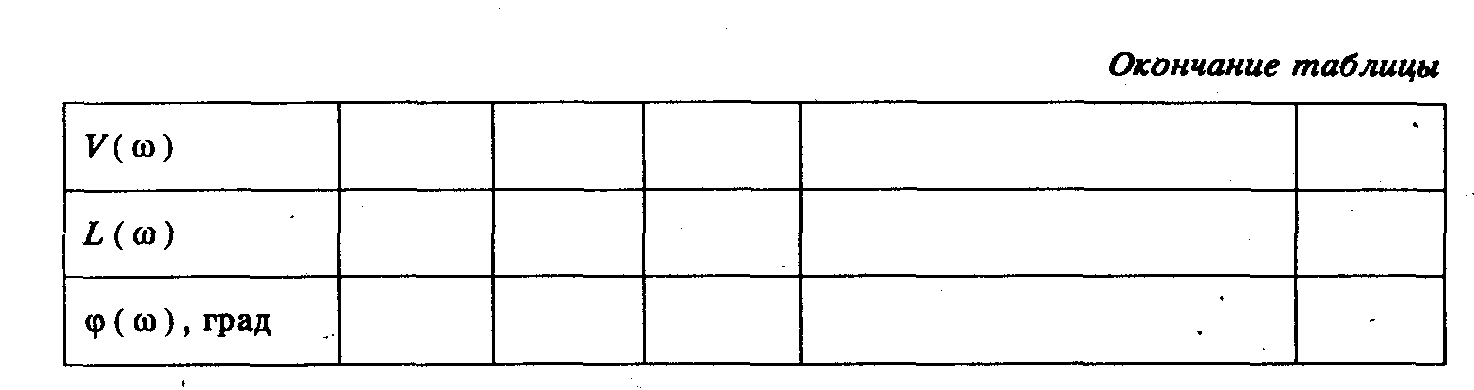
Прежде чем нанести на оси абсцисс и ординат масштабы необхо­димо определить (по данным из таблиц) максимальные значения и знаки откладываемых по этим осям параметров, что позволит более рационально использовать бумагу, отведенную для построения графи­ков. Недопустимо, когда при значительной протяженности осей абс­цисс и ординат график занимает мало места вблизи начала координат, или когда отдельным квадрантам систем-координат отводится боль­шая площадь, а графики или не заходят в эти квадранты, или занима­ют в процентном отношении незначительную, площадь.

8. По окончании всех расчетов и построения графиков необходимо провести анализ результатов как по каждому звену в отдельности, так и по совокупности всех исследований. Результаты анализа исследова­ний характеристик отдельных звеньев излагаются после фактического материала (расчетов и графиков) и должны содержать описание пол­ученных характеристик, влияние численных значений коэффициентов дифференциальных уравнений на основные параметры характеристик, а также перечень характерных свойств и специфических особенностей данного звена. Здесь же целесообразно показать, какие преобразова­ния входного сигнала осуществляет звено, и привести пример физи­ческой (технической) реализации исследуемой математической моде­ли (прибор, элемент, устройство и т.п.). В целом анализ результатов, полученных в работе, должен содержать закономерности, выявленные в результате обобщения временных и частотных характеристик иссле­дуемых звеньев (по разным группам звеньев, обладающих общими свойствами).

9. Работа №1 состоит из 19-ти заданий. Количество за­даний и их номера для группы студентов определяет преподаватель с учетом обязательного минимума для всех и дополнительных заданий по желанию отдельных студентов.

Приложение 5 Пассивные корректирующие устройства

Окончание прил. 5

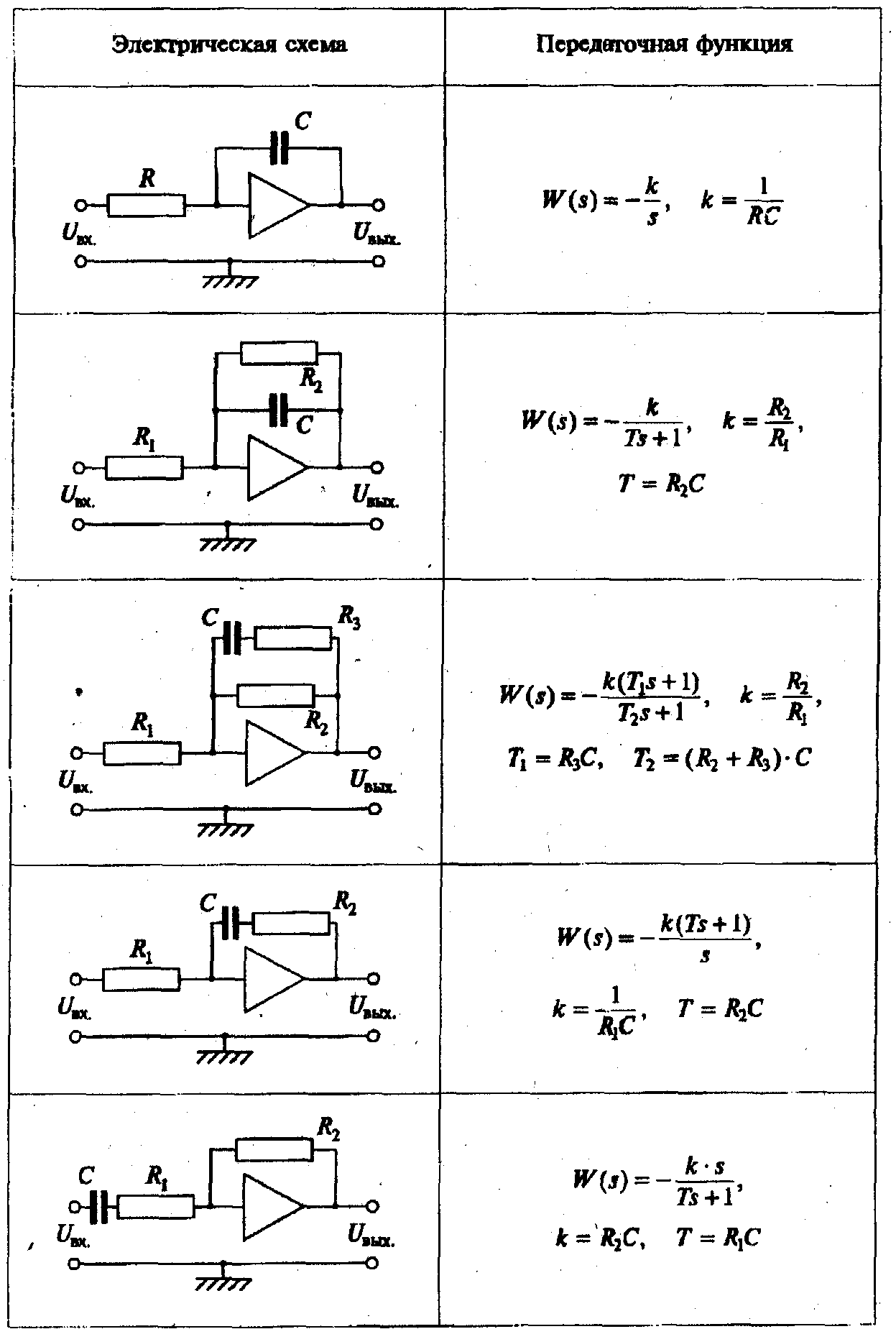
Приложение 9 Дифференциальные уравнения звеньев

Приложение 10 Коэффициенты уравнений 1—4, 9, 11—14

Приложение 11 Коэффициенты уравнений б—8, 10,. 15

Окончание прил. 11

Приложение 12 Коэффициенты уравнений 5

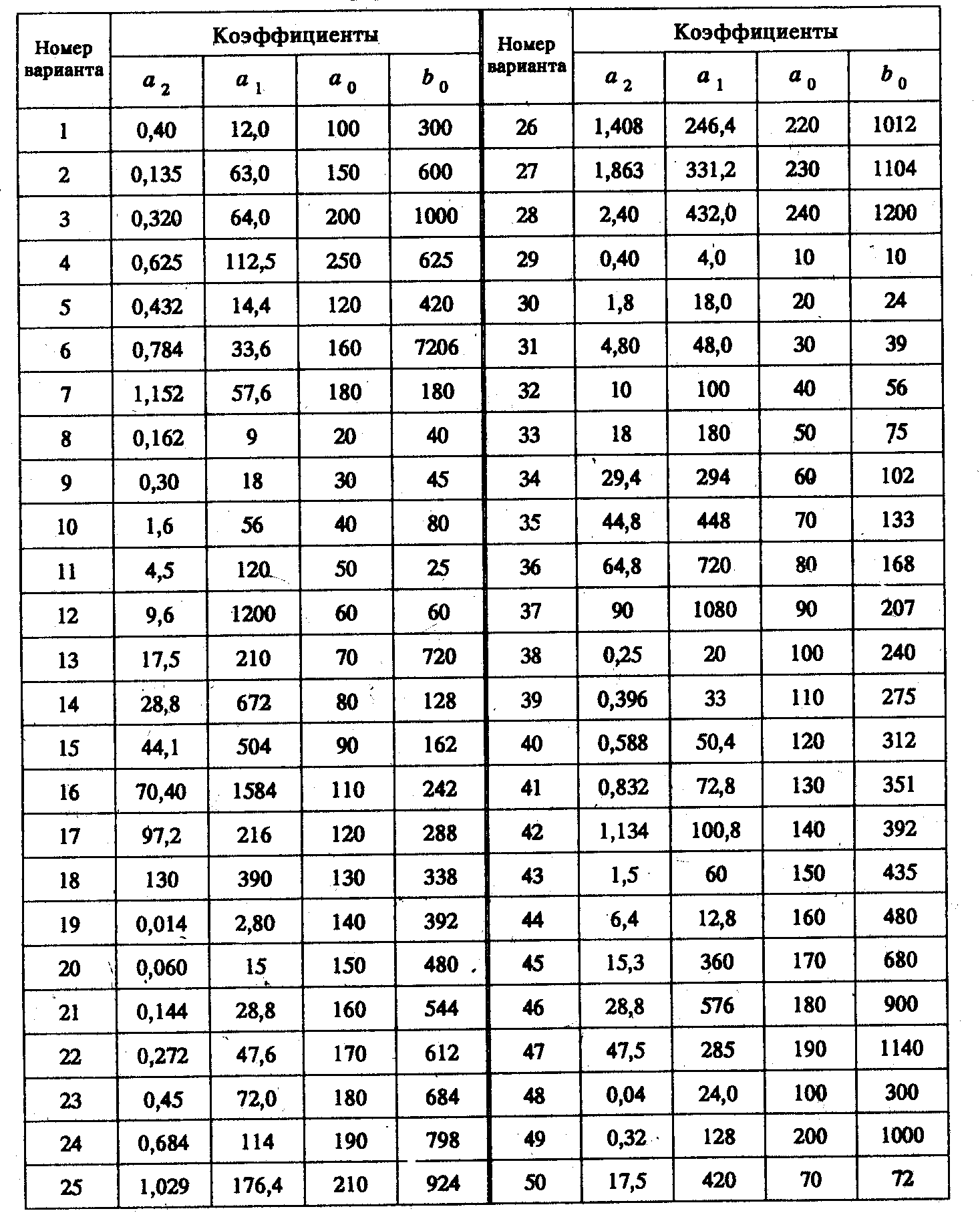
Приложение 13 Значение постоянных времени для уравнений 16—19

Окончание прил. 16

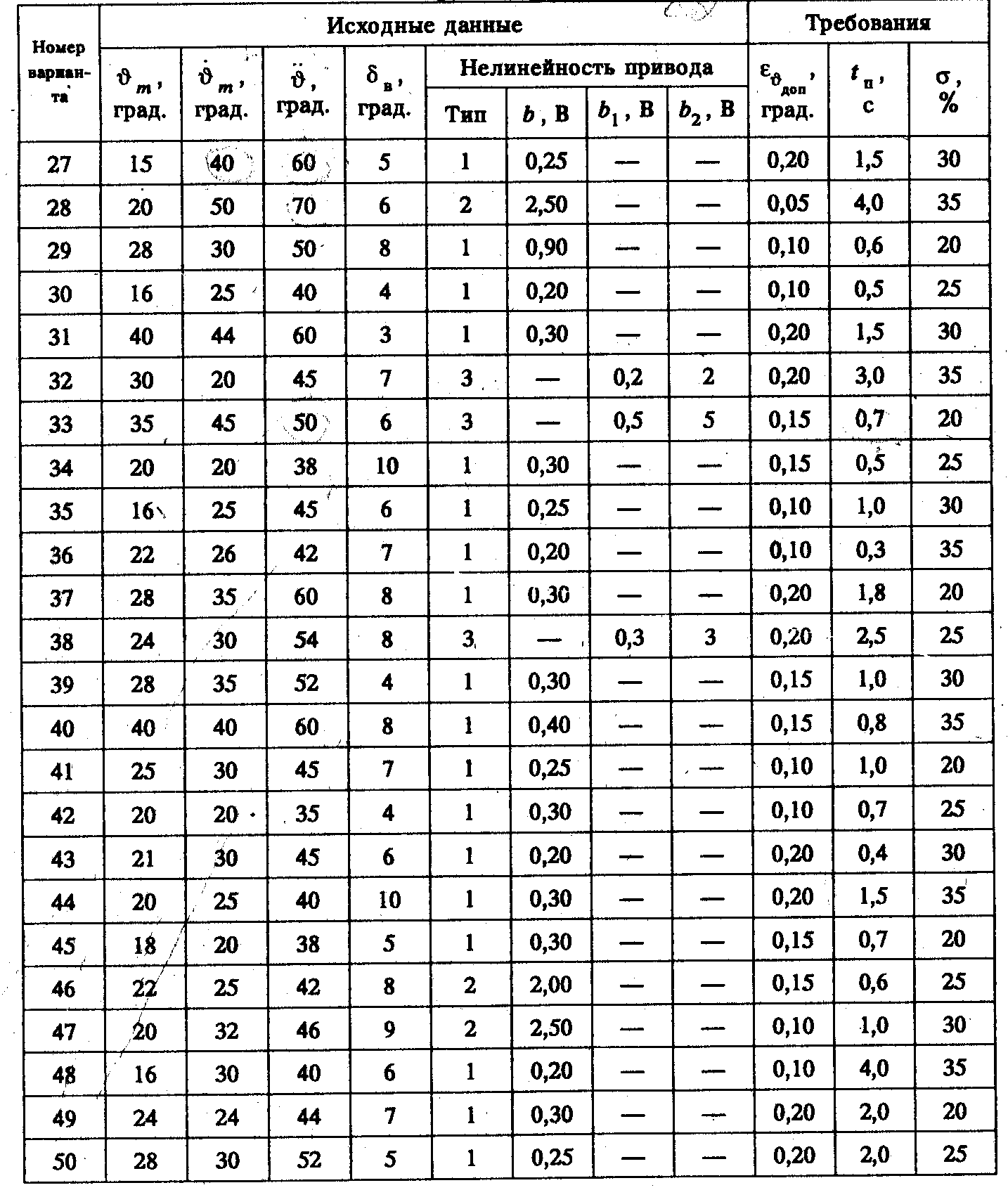
Примечания:

1. Тип нелинейности статической характеристики при­вода см. в приложении №8.

2. Требуемые запасы устойчивости по фазе 30... 60°, по амплитуде 8...12дБ.

ЛИТЕРАТУРА

1. Бесекерский В.А., Попов Е.П. Теория систем автоматического регули­рования. — М.: Наука, 1966. — 992 с.

2 Попов Е.П. Теория линейных система автоматического регулирования и управления. — М.: Наука, 1989. — 302 с.

3. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления. — М.: Наука, 1989. — 226 с.

4. Попов Е.П. Прикладная теория процессов управления в нелинейных си­стемах. — М.: Наука, 1973. — 583 с.

5. Воронов А.А, Основы теории автоматического управления. — М.: Энер­гия, 1966. — 371 с.

6. Техническая кибернетика. Теория автоматического регулирования./Отв. ред. В.В. Солодовников. Кн. 1, 2, 3. — М.: Машиностроение, 1969.

7. Разыграев А.П. Основы управления полетом космических аппаратов. — М.: Машиностроение, 1990. — 480 с.

8. Колчин И.В., Кочетков В.И., Туманов А.В. Оборудование летательных аппаратов. — М.: Машиностроение, 1979. — 152 с.

9. Боднер В.А. Системы управления летательных аппаратов. — М.: Маши­ностроение, 1973. — 504 с.

10. Кузовков Н.Т. Системы стабилизации летательных аппаратов. — М.:

Высшая школа, 1976. — 304 с.