Глава 2. Собственные интегралы, зависящие от параметра

Пусть определена на , и при каждом значении функция интегрируема по Риману на отрезке . Тогда интеграл

(1)

называют собственным интегралом, зависящим от параметра . Наряду с интегралами вида (1) рассматривают интегралы более общего вида

, (2)

и определены на множестве , и их значения принадлежат .

2.1. Непрерывность интеграла по параметру

Теорема 1. Если непрерывна в прямоугольнике , тогда непрерывна на . В частности, если непрерывна в прямоугольнике и , то

,

то есть, возможен предельный переход под знаком интеграла.

Теорема 2. Пусть функция непрерывна в прямоугольнике , а функции и непрерывны на отрезке , тогда непрерывна на .

2.2. Дифференцирование по параметру

Теорема 3. (I правило Лейбница).Если и непрерывны на , то дифференцируема на и имеет место формула

.

Теорема 4. (II правило Лейбница).Пусть и непрерывны на , а , имеют непрерывные производные на . Тогда тоже имеет производную на , причем

2.3. Интегрирование по параметру

Теорема 5. Если функция непрерывна в прямоугольнике , то интегрируема на отрезке , и справедливо равенство

.

2.4.Контрольные вопросы и задания

1. Дайте определение собственного интеграла, зависящего от параметра.

2. При каких условиях интеграл, зависящий от параметра, является непрерывной функцией?

3. Найти .

4. Доказать, что функция непрерывна на .

5. Найти , если .

6. Можно ли вычислить по правилу Лейбница , если при .

2.5.Образцы решения типовых задач

Пример 1. Вычислить .

Так как функция непрерывна на , можно применять теорему о непрерывности собственного интеграла с параметром. Имеем

.

Пример 2. Можно ли совершить предельный переход под знаком интеграла

.

Нет, нельзя. Переходя к пределу под знаком интеграла, получим ноль. Если вычислить интеграл, а затем перейти к пределу, то получим

.

Так как в точке функция терпит разрыв, теорему о предельном переходе применять нельзя.

Пример 3. Вычислить .

Рассмотрим функцию . Она непрерывна на прямоугольнике . Применяя теорему об интегрировании собственного интеграла по параметру, имеем

,

так как . Но так как , то .

Пример 4. Найти , если .

Так как функция непрерывно дифференцируема на , -непрерывно дифференцируемы на , непрерывна на , то

.

Глава 3. Несобственные интегралы, зависящие от параметра

3.1. Сходимость. Равномерная сходимость

Пусть определена на и при каждом функция интегрируема по Риману на любом отрезке , и сходится. Тогда этот интеграл представляет собой функцию , определенную на множестве .

Определение 1. Если для каждого интеграл сходится, то интеграл называется сходящимся на множестве .

Условия при которых для несобственных интегралов, зависящих от параметра, справедливы теоремы, аналогичные для собственных интегралов, основаны на понятии равномерной сходимости интеграла.

Определение 2. Сходящийся на множестве интеграл называется равномерно сходящимся на этом множестве, если для любого существует такое ), что для всех и всех выполняется неравенство

.

В этом определении следует отметить аналогию с функциональными рядами 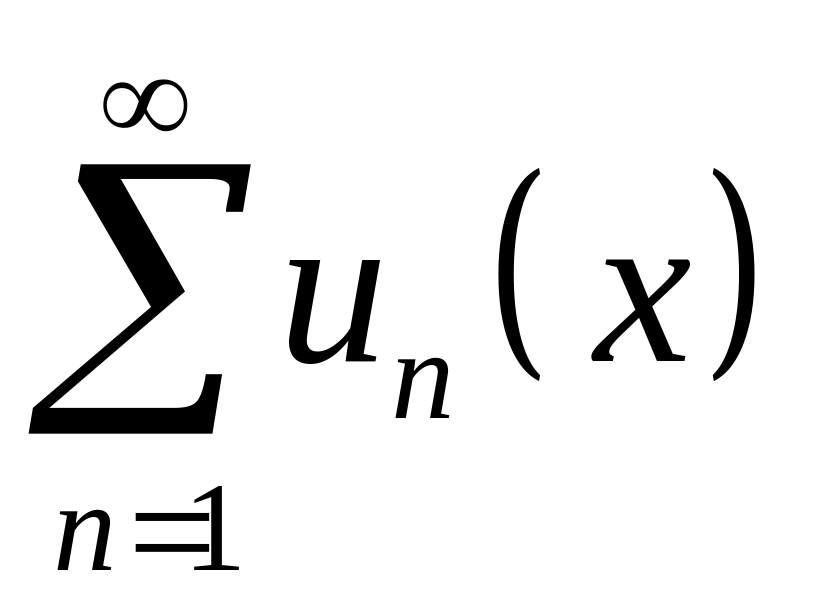. Равномерная сходимость функционального ряда равносильна равномерному стремлению к нулю остатка ряда .

Теорема 1. (Критерий Коши равномерной сходимости) Для того, чтобы несобственный интеграл равномерно сходился на множестве , необходимо и достаточно, чтобы для любого существовало такое , что для всех и , удовлетворяющих условиям и и для всех выполнялось неравенство

.

Теорема 2. (sup-критерий равномерной сходимости) Для того, чтобы несобственный интеграл равномерно сходился на множестве , необходимо и достаточно, чтобы

Пример.

.

. Интеграл сходится на множестве неравномерно.

На множестве , сходимость равномерная, так как

.