80. Моделирование нейронов мозга. Многослойные персептроны. Алгоритмы обучения. Задача аппроксимации функции.

Способностью нейрона является прием, обработка и передача электрических сигналов по нервным путям, которые создают коммуникационную систему мозга.

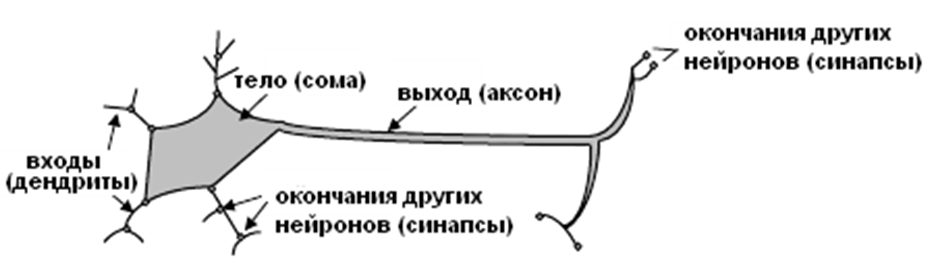
Рисунок 1. Биологический нейрон

Формальный нейрон (первая модель предложена в 1943 г. У. Мак-Каллоком и В. Питтсом) – это элемент обладающий, следующими свойствами:

• он может находиться в одном из двух устойчивых состояний («возбужден» - «невозбужден»), соответственно на выходе – 1 или 0;

• для возбуждения нейрона необходимо подать на его входы некоторое количество сигналов, число которых превышает порог возбуждения;

• порог возбуждения предполагается неизменным;

• имеются 2 вида входов: возбуждающие и тормозящие;

• возбуждение любого тормозящего синапса предотвращает возбуждение нейрона, независимо от числа возбуждающих сигналов;

• имеет место временная задержка прохождения сигналов в синапсах.

В 1952г. Мак-Каллок усовершенствовал эту модель. В новой модели тормозящие входы эквивалентны возбуждающим. Допускается флуктуация порога возбуждения. Ещё одно важное отличие – введение запрещающего входа, осуществляющего взаимодействие между входами нейрона.

Схема формального нейрона Мак-Каллока-Питтса для случая бинарных сигналов (без тормозящих входов и учета задержки) (f(s) – функция активации):

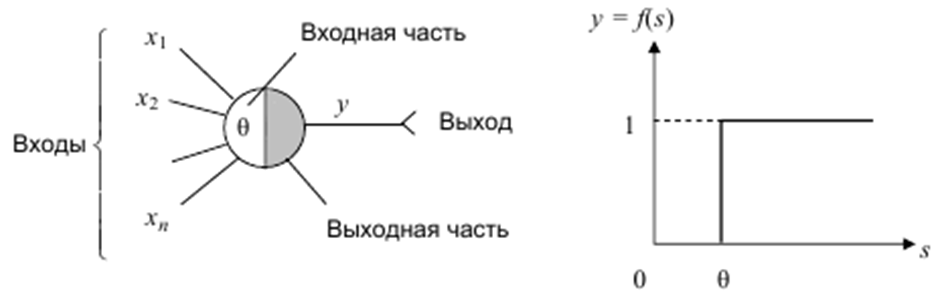
Условие возбуждения нейрона: , - порог возбуждения нейрона, s – суммарное возбуждение нейрона, х_i – значение i-го входа, .

Каноническая форма схемы нейрона:

- дополнительный вход – смещение (bias);

- веса входов ; ; порог возбуждения принят = 0 ( ).

Т. о. условие возбуждения формального нейрона:

или .

Теорема. Для любого логического выражения, удовлетворяющего некоторым условиям, можно найти нейронную сеть составленную из формальных нейронов, поведение которой описывается данным логическим выражением.

Обобщенная модель искусственного нейрона:

На нейрон поступает набор входных сигналов . Каждый входной сигнал x_i умножается на соответствующий ему вес w_i и поступает на суммирующий блок ( ). Там вычисляется уровень активности s нейрона: . Реакция на выходе нейрона определяется путем пропускания сигнала S через нелинейную функцию f. Функция f(S) называется функцией активации нейрона и удовлетворяет условиям: а) - ограниченность функции; б) - монотонная (обычно неубывающая) функция аргумента s.

В качестве функций активации на практике используют нелинейные функции вида:

а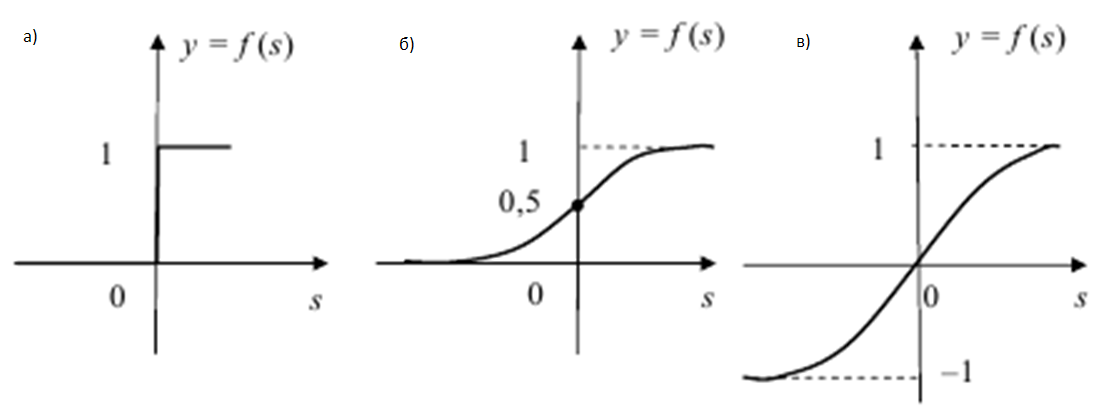 ) пороговая (логическая) функция: .

б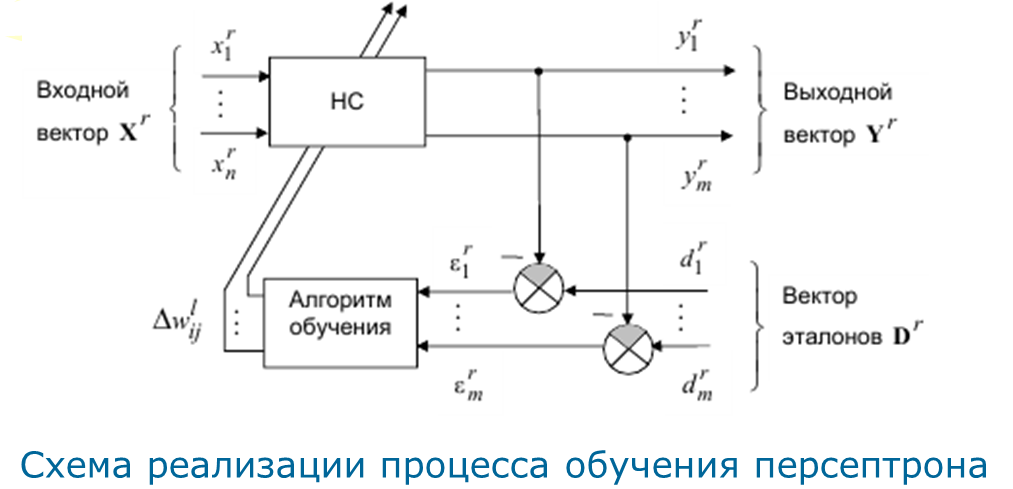 ) сигмоидная (логистическая) функция: .

в) функция гиперболического тангенса: .

Многослойные персептроны – сети прямого распространения (т.е. без обратных связей).

П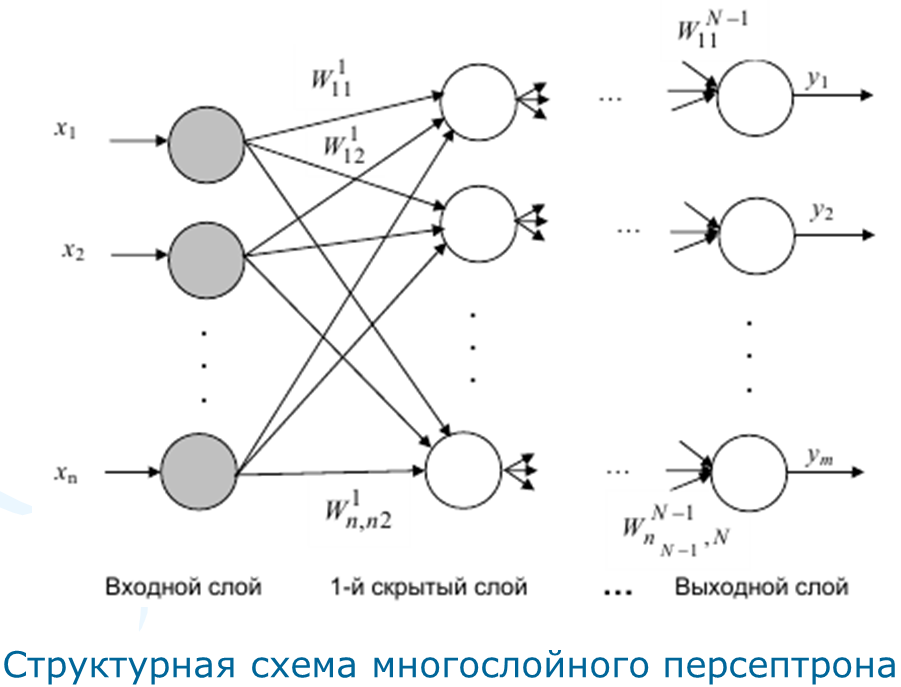 усть набор входных сигналов нейронов -го слоя; - матрица весов синаптических связей, соединяющих нейроны -го слоя с нейронами -го слоя, . Тогда работа персептрона описывается следующими уравнениями:

• для входного слоя ( =1): 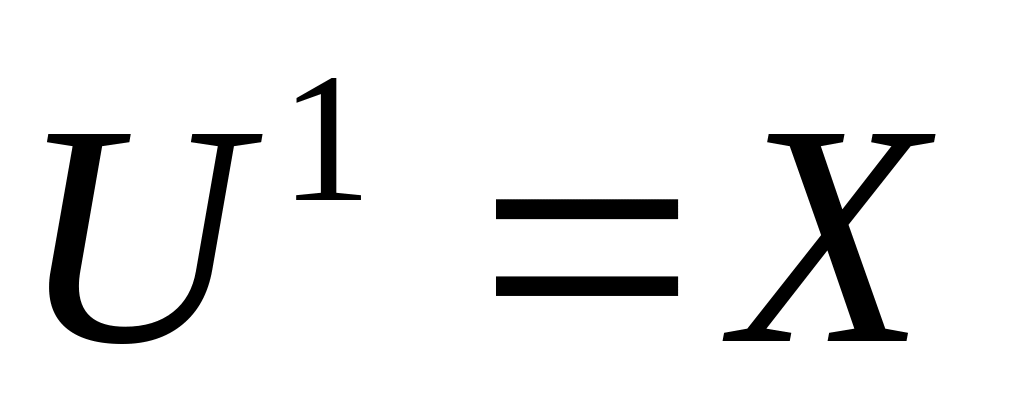, где 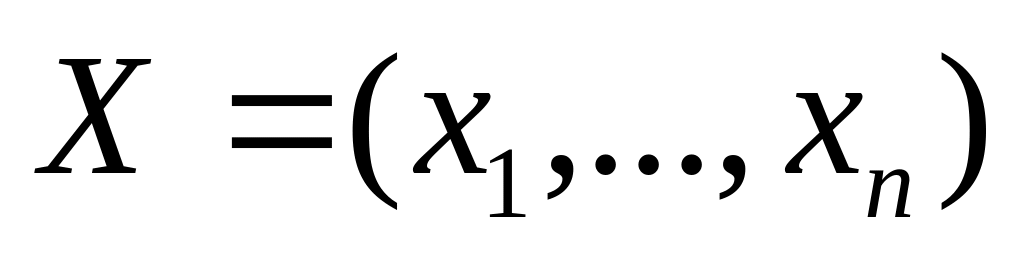- входной вектор.

• для 1-ого скрытого слоя ( =2): ;

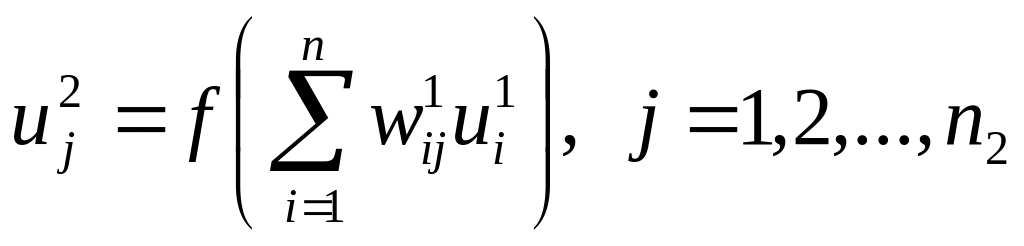• для 2-ого скрытого слоя ( =3): ;

... … … … … … … … …

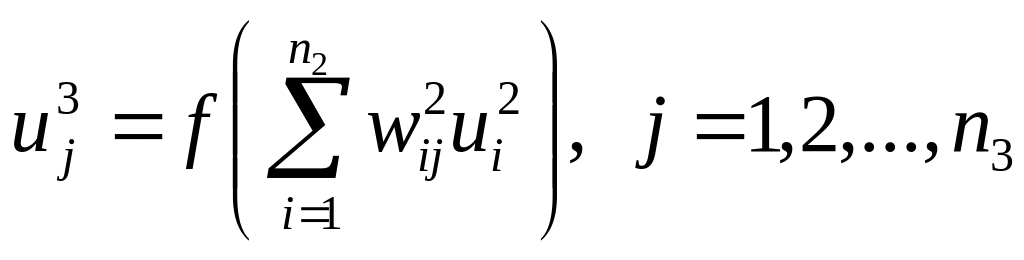• для входного слоя ( =N): .

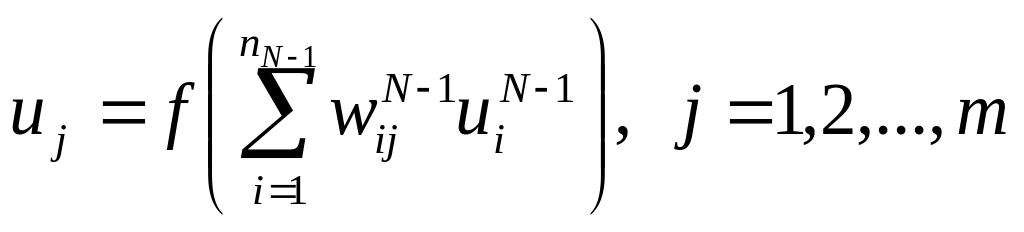- число нейронов -го слоя ( ); N – число слоев НС; - функция активации нейрона.

Выбрав соответствующим образом веса синаптических связей можно обеспечит желаемые характеристики «вход-выход» персептрона в целом.

Процедура нахождения весов синаптических связей называется обучением нейронной сети. Процедура обучения сети:

1. инициализируются случайным образом веса синаптических связей НС.

2. на входы НС поочередно подаются «образы» (входные векторы) 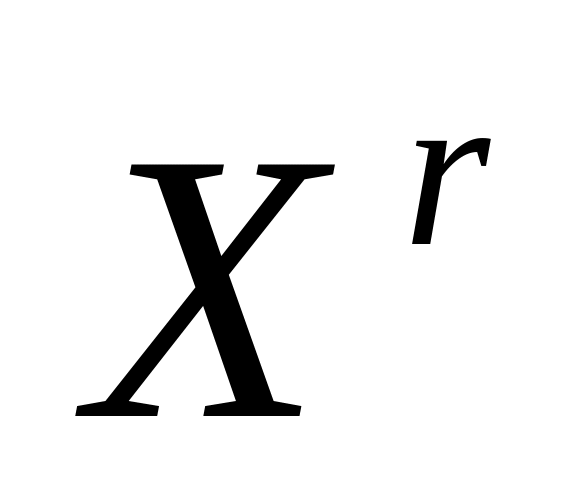из обучающей выборки 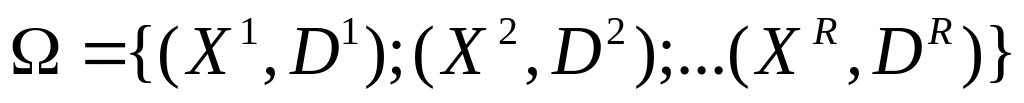, - желаемая реакция (вектор «эталонов») НС.

3. вычисляется реакция 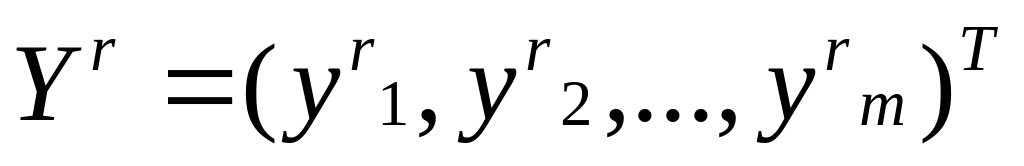НС.

4. вычисляется вектор ошибки сети

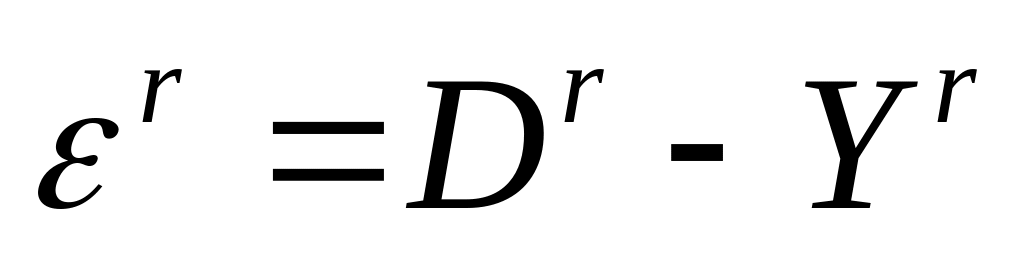
5. вычисляется суммарная квадратичная ошибка

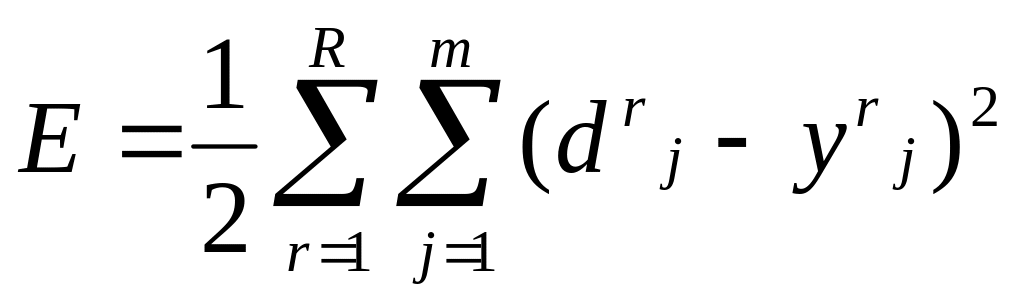
6. проверка выполнения условия 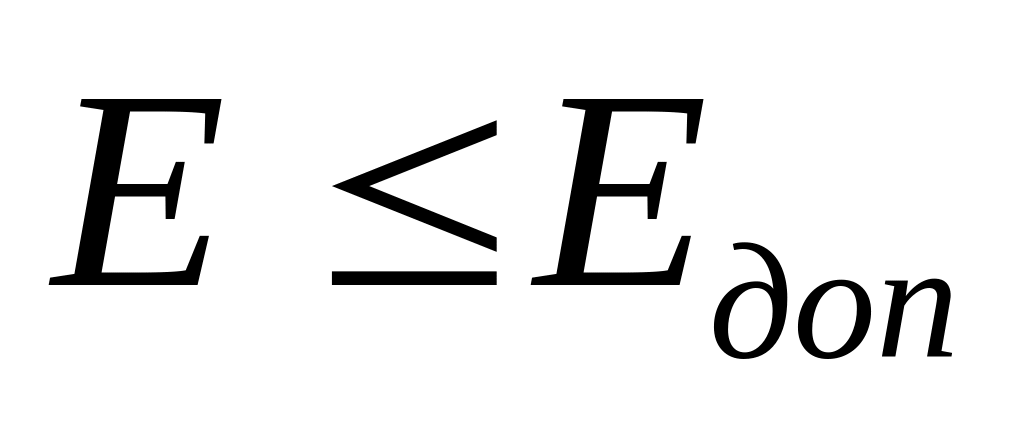, где 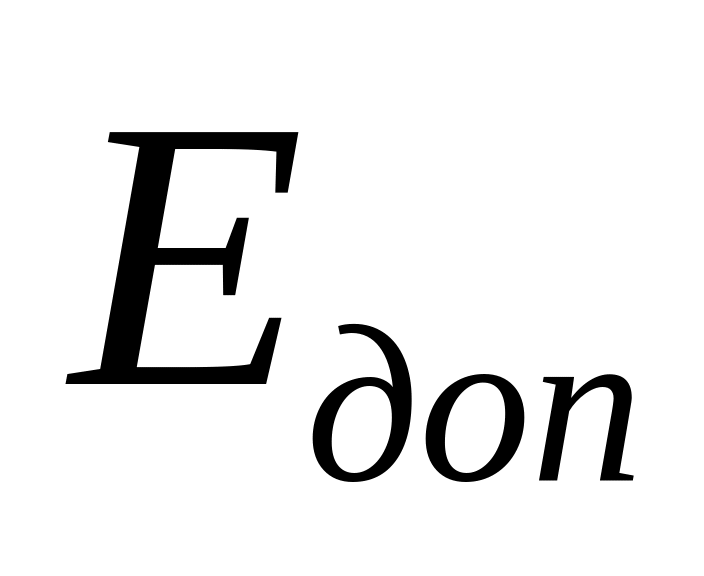- заданное малое (допустимое) значение ошибки. Если условие выполняется, то обучение НС законченно, иначе переходим к следующему шагу

7. производится изменение весов НС в направлении уменьшения ошибки обучения ( 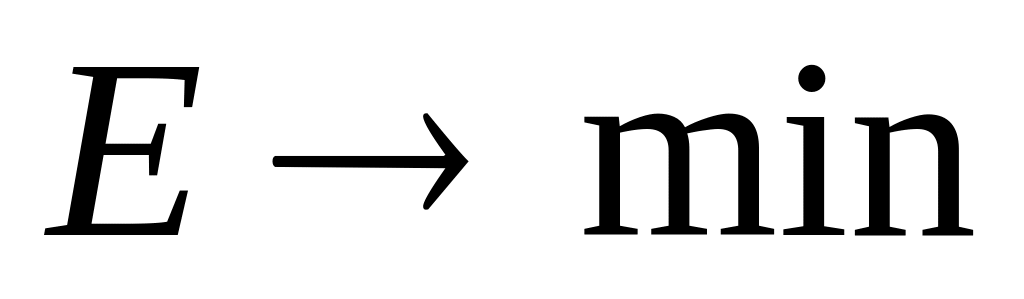), после чего – переход к шагу 2.

Наиболее простой способ настройки весов НС – использование градиентного алгоритма минимизации ошибки Е: .

Алгоритмы обучения НС

Алгоритм обратного распространения: Суть алгоритма – подстройка весов синаптических связей послойно, начиная с последнего (выходного) и заканчивая 1-м слоем.

Пусть обучающая выборка состоит из одной пары (X,D), т.е. R=1, тогда:

• для выходного слоя: ;

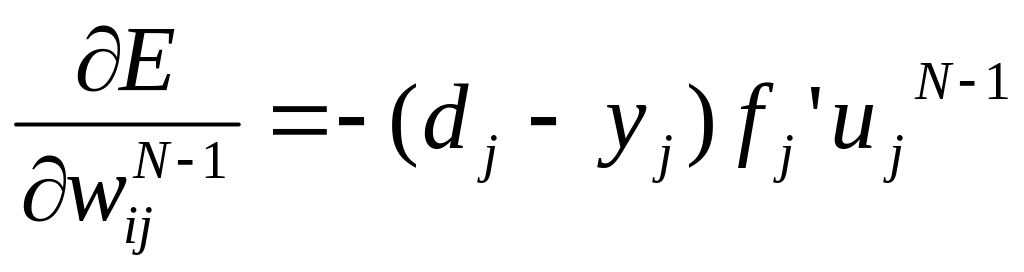• для последнего скрытого слоя: 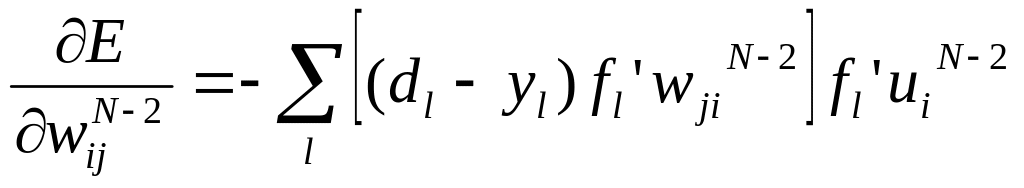; и т.д.

Пусть функция активного нейрона - сигмоидная функция. Тогда и получаем:

• для выходного слоя: ;

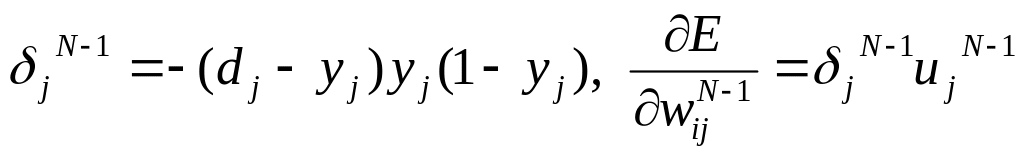• для последнего скрытого слоя: … … … … … … … … … … … … … … … … … … … … … … … … … … … …

• для первого скрытого слоя:

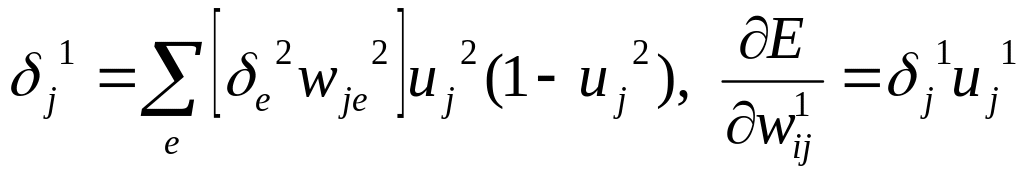
Т. о., приращение силы связи пропорционально произведению сигнала ошибки и выходного сигнала -го слоя. Вычисляя и слой за слоем по направлению ко входу, можно скорректировать все веса НС.

Задача аппроксимации функции

Теорема (А.Н. Колмогоров): Любая непрерывная функция n переменных может быть представлена в виде суммы конечного числа одномерных функций : 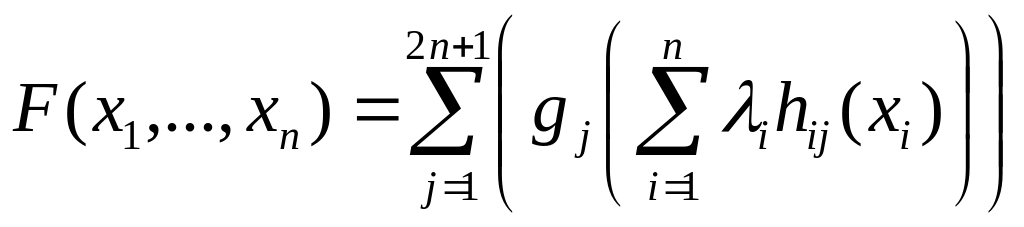, где и - непрерывные и одномерные функции; - постоянные коэффициенты.

Теорема: Любую непрерывную функцию нескольких переменных можно с любой степени точности реализовать с помощью трехслойного (считая входной слой) персептрона, имеющего достаточное количество нейронов в скрытом слое.