
- •77. Нечеткие множества и лингвистические переменные. Операции над нечеткими множествами.
- •78. Нечеткие алгоритмы. Общие принципы построения нечетких алгоритмов управления динамическими объектами.
- •79. Процедура синтеза нечетких регуляторов. Синтез адаптивной сау с эталонной моделью на основе нечеткой логики. Нечеткий регулятор Такаги-Сугено.
- •80. Моделирование нейронов мозга. Многослойные персептроны. Алгоритмы обучения. Задача аппроксимации функции.
- •81. Архитектуры нейронных сетей: радиально-базисные сети; нейронные сети Хопфилда; нейронные сети Кохонена; рекуррентные нейронные сети.
- •82. Общие принципы построения нейросетевых систем управления динамическими объектами. Применение нейронных сетей в задачах идентификации динамических объектов.
- •83. Стандартный генетический алгоритм. Пример оптимизации с помощью генетического алгоритма. Модификации генетических алгоритмов и особенности их применения.
- •84. Генетическое программирование. Особенности реализации генетического программирования. Практические примеры построения систем управления с использованием генетических алгоритмов.
78. Нечеткие алгоритмы. Общие принципы построения нечетких алгоритмов управления динамическими объектами.
Под нечетким алгоритмом понимается упорядоченное множество нечетких инструкций (правил), в формулировке которых содержатся нечеткие указания (термы). Например, нечеткие алгоритмы могут включать в себя инструкции типа:
«х = очень малое»;
«х приблизительно равно 5»;
«слегка увеличить х»;
«ЕСЛИ х находится в интервале [4,9; 5,1], ТО выбрать y в интервале [9,9; 10,1]»;
«ЕСЛИ х – малое, ТО y – большое, ИНАЧЕ у – небольшое».
Использованные здесь термы «очень малое», «приблизительно равно», «слегка увеличить», «выбрать в интервале» и т.п. отражают неточность представления исходных данных и неопределённость, присущую самому процессу принятия решений.
Две последние инструкции (г-д) представляют собой правила (или нечеткое высказывание), построенные по схеме логической импликации «ЕСЛИ – ТО», где условие «ЕСЛИ» соответствует принятию лингвистической переменной х некоторого значения Ai, а вывод (действие) «ТО» означает необходимость выбора значения Bi для лингвистической переменной у:
ЕСЛИ х – это Ai, ТО y – это Bi.
Общие принципы построения нечетких алгоритмов управления динамическими объектами
Схема системы нечеткого управления:
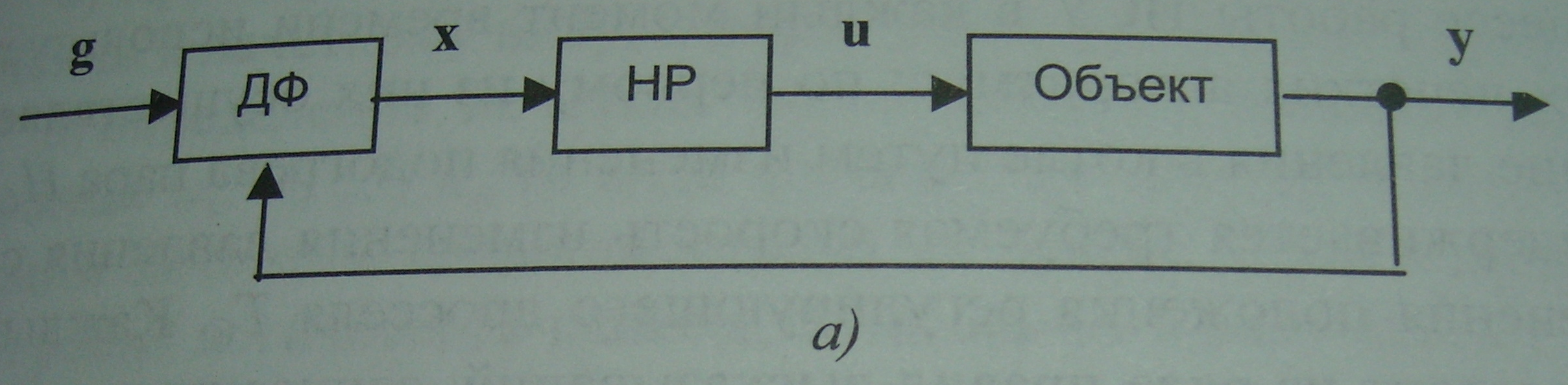 Рис.
3.
Рис.
3.
ДФ – динамический фильтр (выделяет сигналы ошибок управления),
НР – нечеткий регулятор (включает базу правил и механизм логического вывода).
Нечеткое управление - стратегия управления, основанная на эмпирически приобретённых знаниях относительно функционирования объекта (процесса), представленных в лингвистической форме в виде некоторой совокупности правил.
Схема нечеткого регулятора в общем виде принимает вид, изображенный на рис. 4.
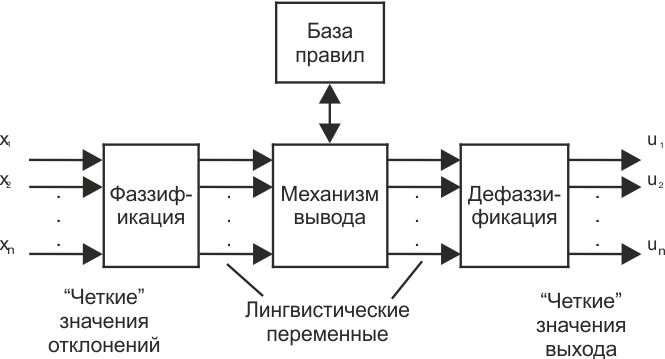 Рис.
4.
Рис.
4.
Как
видно из данной схемы, формирование
управляющих воздействий
![]() включает в себя следующие этапы:
включает в себя следующие этапы:
получение отклонений управляемых координат и скоростей их изменений –
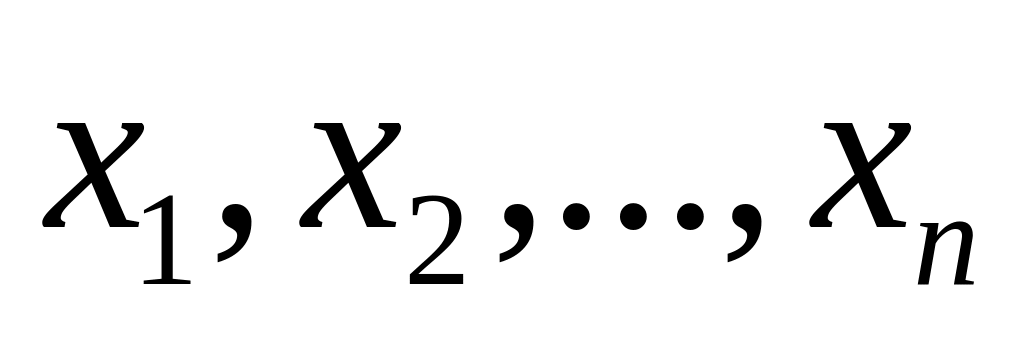 ;
;«фаззификация» этих данных, т.е. преобразование этих значений к нечеткому виду, в форме лингвистических переменных;
определение нечетких (качественных) значений выходных переменных (в виде функций их принадлежности соответствующим нечетким подмножествам) на основе заранее сформулированных правил логического вывода, записанных в базе правил;
«дефаззификация», т.е. вычисление реальных числовых значений выходов используемых для управления объектом.
79. Процедура синтеза нечетких регуляторов. Синтез адаптивной сау с эталонной моделью на основе нечеткой логики. Нечеткий регулятор Такаги-Сугено.
Обобщенная процедура синтеза нечетких алгоритмов управления может быть сформулирована следующим образом:
определяется множество целей, которые ставятся перед системой (какие конечные результаты преследует создание системы?);
уточняются множества входных и выходных переменных регулятора (какие координаты объекта должны наблюдаться и какие управляющие воздействия должны изменяться для того, что бы достичь поставленных целей?);
перечисляются возможные ситуации в работе системы (как должны выбираться лингвистические переменные и какие значения (термы) они могут принимать?);
формируется база правил (какой набор правил отражает желаемые изменения состояния системы?);
производится выбор методов фаззификации;
конкретизируется механизм вывода и методы дефаззификации (по каким зависимостям входы нечеткого регулятора должны преобразовываться в его управляющее воздействие?).
Синтез адаптивной САУ с эталонной моделью на основе нечеткой логики
Качество
процессов управления при использовании
ПИД-регуляторов существенно зависит
от выбора его коэффициентов усиления![]() для пропорциональной, интегральной и
дифференциальной составляющей
соответственно.
для пропорциональной, интегральной и
дифференциальной составляющей
соответственно.
Допустим, что структурная схема адаптивной системы управления с эталонной моделью имеет вид как на рис. 1.
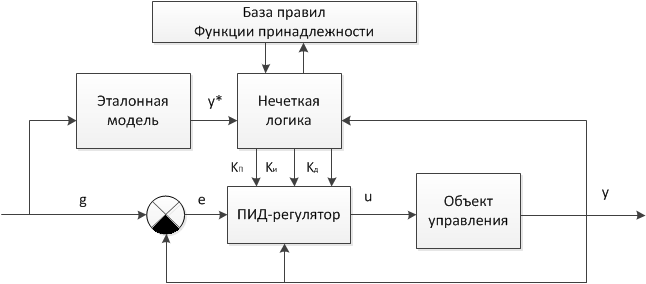 Рисунок
1.
Рисунок
1.
Уравнение основного ПИД-регулятора здесь имеет вид:
![]() .
.
Будем учитывать 3 таких показателя:
время достижения уровня, равного 10% от установившегося значения выходной величины (
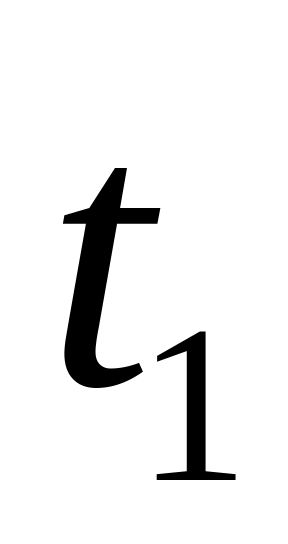 );
);время нарастания, т.е. время достижения уровня 90% от установившегося значения (
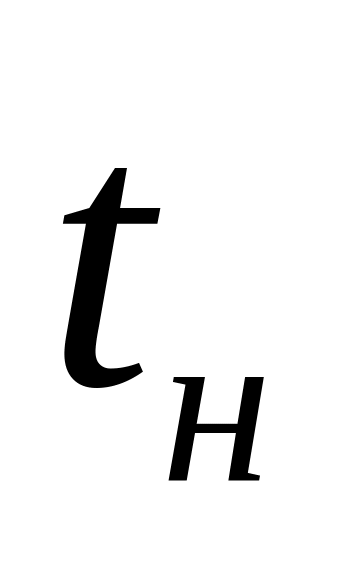 );
);перерегулирование (
 ).
).
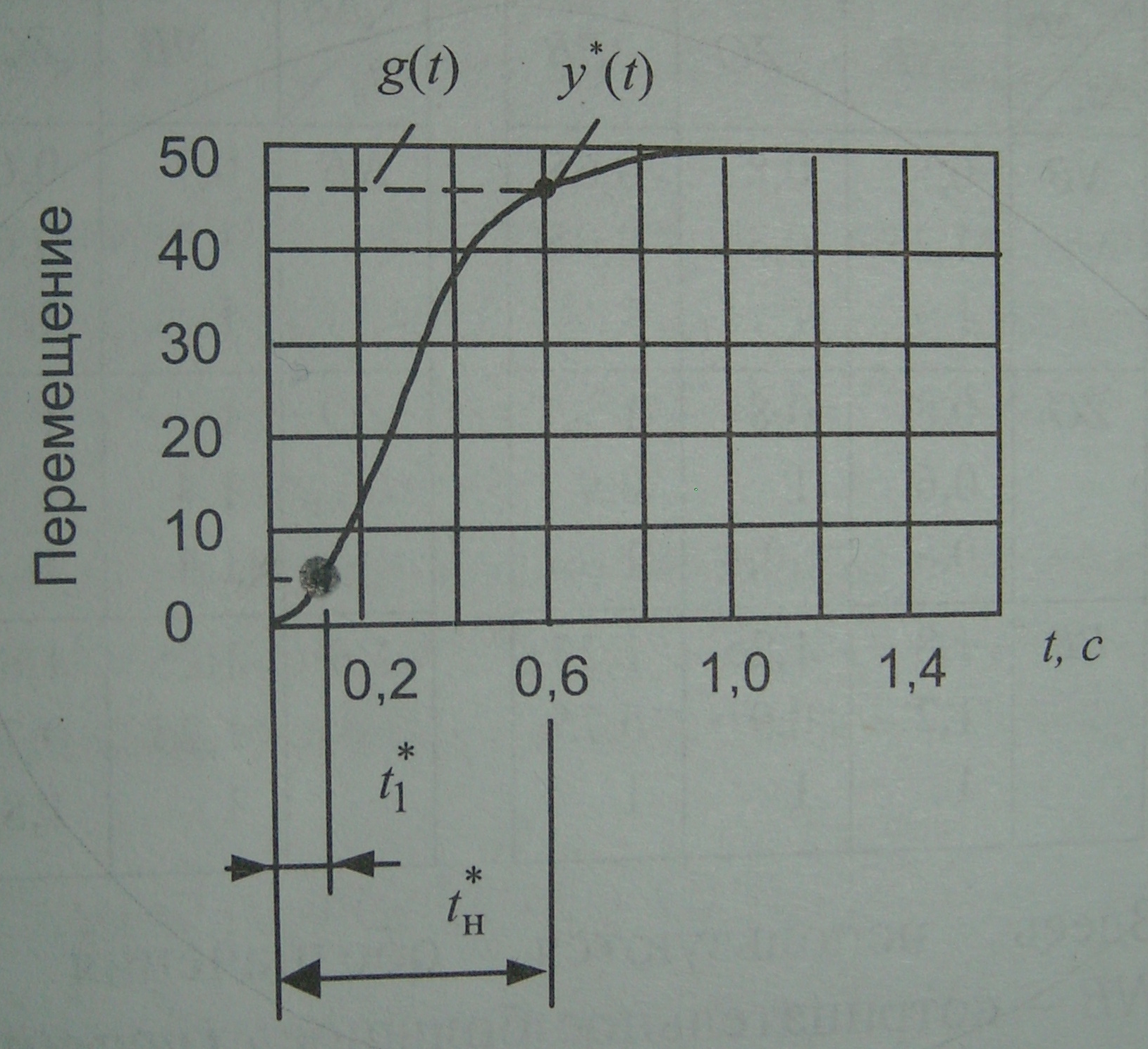
и
показаны на рис. 2.,
=
0 поскольку в качестве
![]() выбран монотонный переходной процесс.
выбран монотонный переходной процесс.
 Рисунок
2.
Рисунок
2.
Будем
полагать, что цель, поставленная перед
нечетким регулятором, - обеспечить
желаемые показатели качества системы
![]() ,
,
![]() ,
,
![]() за счет подстройки параметров основного
регулятора
за счет подстройки параметров основного
регулятора
![]() .
При этом учитывается следующий опыт:
.
При этом учитывается следующий опыт:
если
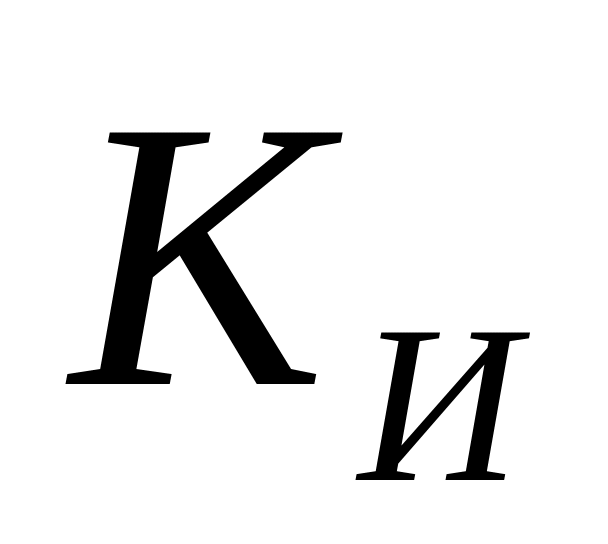 увеличивается, то
уменьшается, а
возрастает;
увеличивается, то
уменьшается, а
возрастает;если
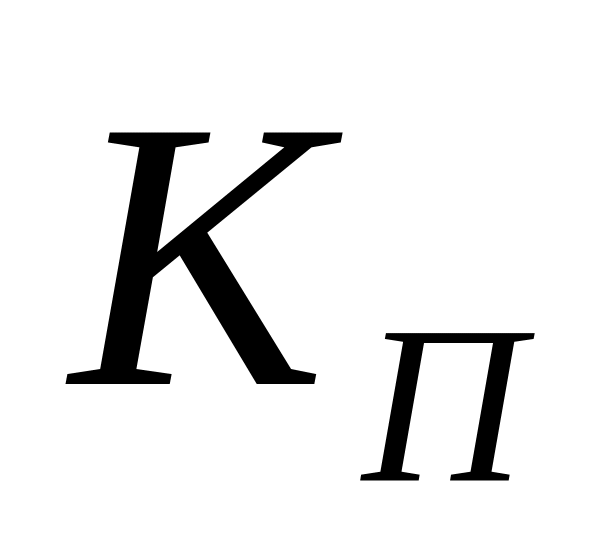 увеличивается, то
сильно уменьшается, а
возрастает;
увеличивается, то
сильно уменьшается, а
возрастает;если
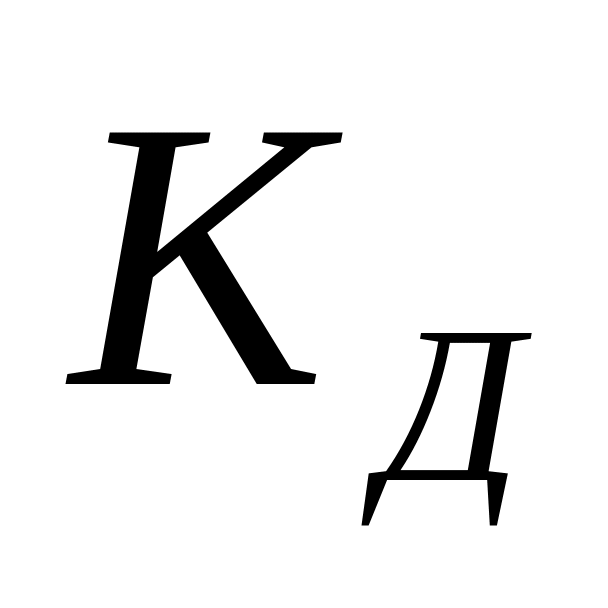 увеличивается, то
сохраняется, а
слегка возрастает;
увеличивается, то
сохраняется, а
слегка возрастает;что бы уменьшить , необходимо уменьшить и одновременно увеличить .
В
качестве входов нечеткого регулятора
(НР) будем рассматривать отклонения
![]() ,
,
![]() ,
,
![]() ,
а под выходами НР будем понимать
коэффициенты
.
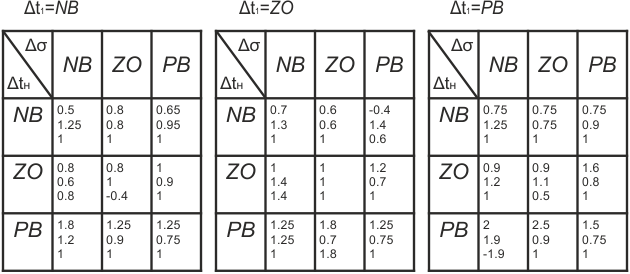
База правил отображена на рис. 3 (она
построена на основе мнений экспертов).
,
а под выходами НР будем понимать
коэффициенты
.
База правил отображена на рис. 3 (она
построена на основе мнений экспертов).
 Рисунок
3.
Рисунок
3.
NB – «отрицательное небольшое»; ZO – «около нуля»; PB – «большое положительное».
 Рисунок
4.
Рисунок
4.
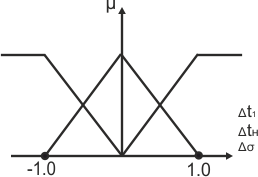
Соответствующие
этим термам функции принадлежности
входных переменных НР (после нормирования
диапазонов изменений указанных величин
![]() ,
,
![]() ,
,
![]() ).показаны
на рис. 4.
).показаны
на рис. 4.
В
каждой из клеток таблицы, составленной
для различных значений переменной
,
записаны значения поправочных
коэффициентов
![]() ,
определяющих требуемый закон изменения
параметров ПИД-регулятора в зависимости
от значений входных лингвистических
переменных НР:
,
определяющих требуемый закон изменения
параметров ПИД-регулятора в зависимости
от значений входных лингвистических
переменных НР:
![]() .(1.1)
.(1.1)
Например:
ЕСЛИ
=NB
И
![]() =NB
И
=NB,
ТО (
=NB
И
=NB,
ТО (![]() ),
т.е. в случае затянутого слабо
демпфированного переходного процесса
y(t),
необходимо на 50% увеличить КИ,
на 25% снизить КП,
сохраняя неизменным значение КД.
),
т.е. в случае затянутого слабо
демпфированного переходного процесса
y(t),
необходимо на 50% увеличить КИ,
на 25% снизить КП,
сохраняя неизменным значение КД.
Таким образом, измеренные значения отклонений , , после их фаззификации м помощью приведенных на рис. 4 функций принадлежности подвергаются обработке с использованием записанных в таблице (рис. 3) правил вывода.
Если на данном этапе применить метод Произведения, а для дефаззификации воспользоваться методом центра тяжести, то получаем следующие результирующие значения поправочных коэффициентов :
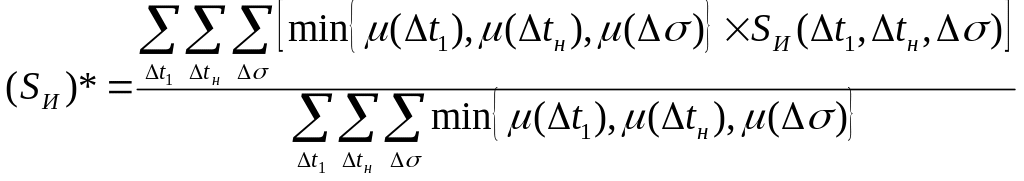
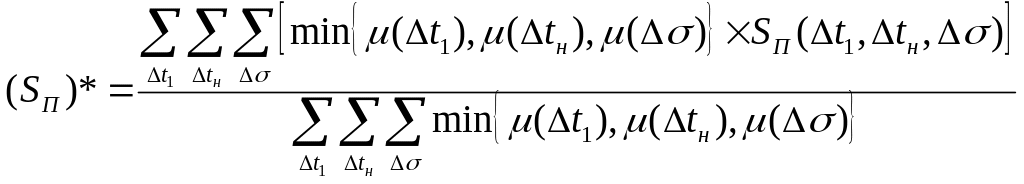
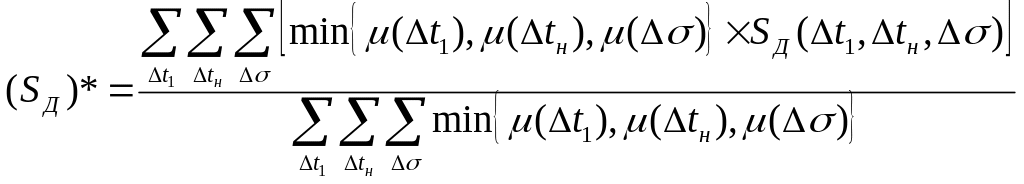 Тройная
сумма в каждом из выражений учитывает,
что любое из измеренных значений
,
,
принадлежит двум соседним нечетким
подмножествам.
Тройная
сумма в каждом из выражений учитывает,
что любое из измеренных значений
,
,
принадлежит двум соседним нечетким
подмножествам.
После
вычисления «четких значений»
![]() необходимо
вычислить
по формулам (1.1).
необходимо
вычислить
по формулам (1.1).
Нечеткий регулятор Такаги-Сугено
Построим НР на базе алгоритма вывода Сугено.
Способ
вычисления выходных переменных
![]() существенно отличается (от обычного
НР), поскольку правила «ЕСЛИ-ТО» в данном
случае принимают вид:
существенно отличается (от обычного
НР), поскольку правила «ЕСЛИ-ТО» в данном
случае принимают вид:
L1: ЕСЛИ x1=A1(1) И … И xn=An(1), ТО

![]()
LN: ЕСЛИ x1=A1(N) И … И xn=An(N), ТО
![]()
Здесь
Aj(р),
(j
= 1,2,…,n;
p
= 1,2,…,N)
– значения лингвистических переменных
![]() ;
N
– число этих значений (нечетких
подмножеств); сkj(p)
– фиксированные числовые переменные
(k
= 0,1,2,…,n);
ui(p)
– составляющая i–го
выхода регулятора
ui,
соответствующая правилу Lp.
;
N
– число этих значений (нечетких
подмножеств); сkj(p)
– фиксированные числовые переменные
(k
= 0,1,2,…,n);
ui(p)
– составляющая i–го
выхода регулятора
ui,
соответствующая правилу Lp.
Отличие от НР Мамдани, правые части «ТО» правил представляют собой «четкие» числа, полученные как линейные комбинации переменных на выходе.
Р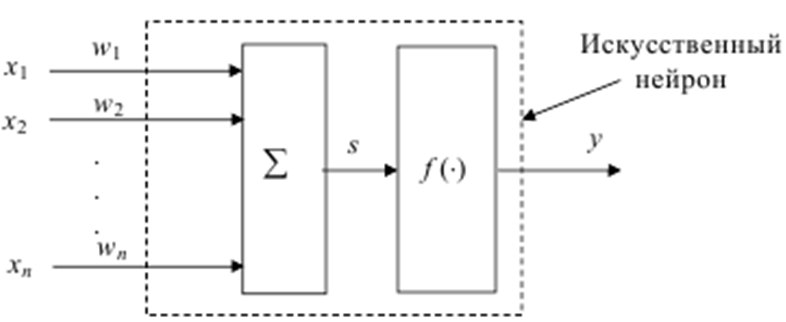 езультирующее
значение i-го
выхода нечеткого регулятора
езультирующее
значение i-го
выхода нечеткого регулятора
![]() находится как взвешенное среднее от
указанных чисел
находится как взвешенное среднее от
указанных чисел
![]() :
:
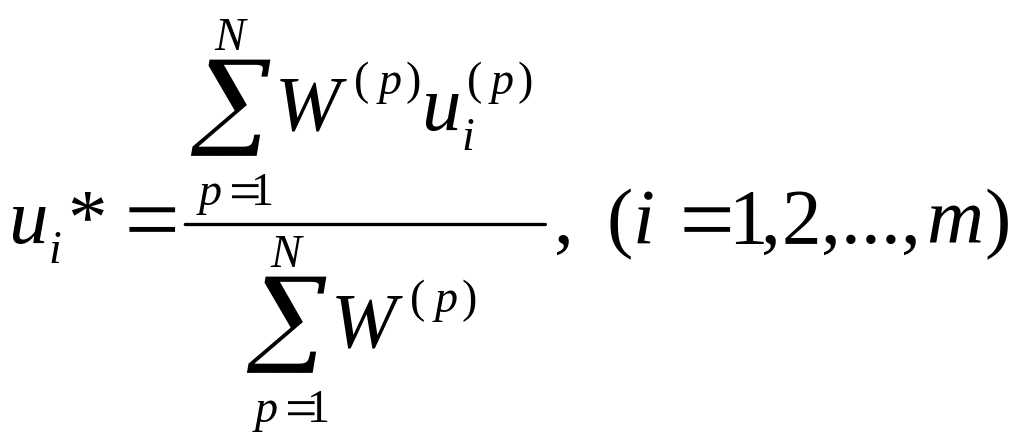 ,
,
где вес W(p) представляет собой уровень активности правила Lp для конкретных значений и вычисляется как:
![]() .
.
Достоинства: компактность системы уравнений, описывающий механизм логического вывода; меньшие вычислительные затраты на реализацию логического вывода, по сравнению с НР Мамдани. Недостатки: «четкий» характер правой части правил является не вполне убедительным приемом совмещения знаний экспертов (левая часть правил) с классическими линейными алгоритмами управления объектом; неоднозначность выбора коэффициентов сkj(p) в правой части правил.
