72. Алгебраическое интерполирование. Исследование существования и единственности интерполяционного полинома. Интерполяционный полином Лагранжа. Оценка остаточного члена.

Пусть имеется значения функци f(x_i) в нектр точках x₀,x₁,x₂,,x_n, x_i  [a,b]   I, x₀=a<x₁<…<x_n=b. Требуется построить функцию g(x), такую что, f(x_i)=g(x_i),     i=0,1,2,,n. (1) Задача построения такой функции g(x) называется задачей интерполяции. Точки x₁,x₂,,x_n называются узлами интерполяции. Как правило, функция g(x) ищется из некоторого наперед заданного класса функций, назовем его V. Если элементами V являются полиномы, то говорят об алгебраической интерполяции, при этом функцию g(x) называют интерполяционным полиномом. Говорят, что задача интерполяции поставлена корректно, если при любых значениях f(x_i),   i=1,2,,n, существует единственная функция g(x) из V, удовлетворяющая условиям (1). Исследуем корректность задачи алгебраической интерполяции. Пусть g(x) = a₀+a₁ x++a_m x^m. Коэффициенты a_i определяются условиями (1), то есть являются решением следующей системы линенйых уравнений _i=0^m a_i  x_jⁱ = f(x_j),   j=0,1,2,,n. (2) При m=n число неизвестных данной системы будет равно числу уравнений в ней, а определитель системы будет иметь вид 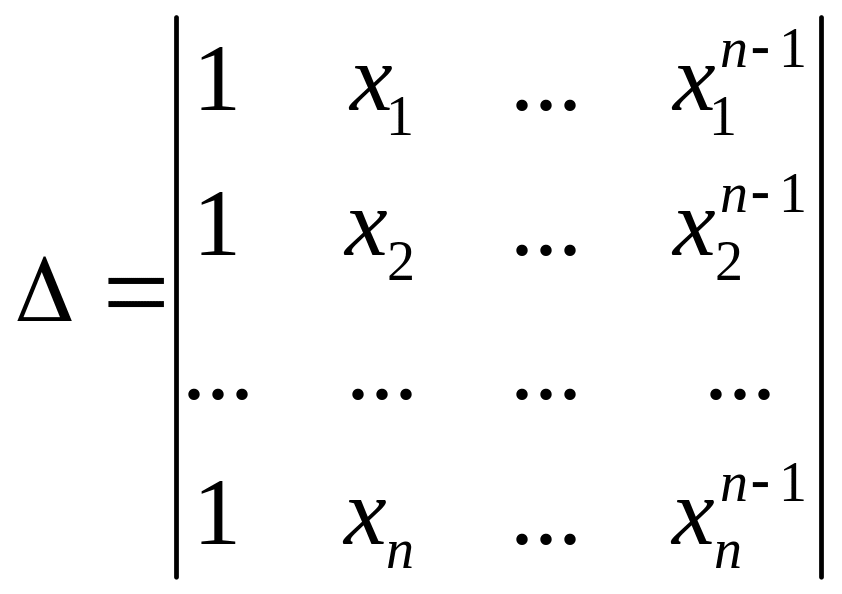Это - определитель Вандермонда, его значение  = _{i > j}  (x_ix_j). Поэтому  отличен от нуля(все узлы интерполяции различны). Итак, задача алгебраической интерполяции корректна, если при заданных n+1 различных узлах интерполяции, функцию f(x) приближать полиномом степени n. Рассмотрим вопрос построения интерполяционного полинома. Его коэффициенты можно найти, решая систему (2). Однако, очевидно что многочлен степени n удовл.условиям (2) имеет вид:

P_n(x) = Сумма(f(x_i) * Ф_i(x)), i=0,n; где Ф_i(x) = Произв.((x-x_i)/(x_i-x_j)); j=0,n; i<>j, i=0,n

(если нужно)

Интерполяционный полином, записанный в такой форме, называют интерполяционным полиномом Лагранжа и обозначают через L_n(x): Оценку погрешности интерполяционного полинома будем проводить в предположении, что функция f(x) имеет непрерывные производные вплоть до порядка n.

Теорема

Пусть f(x) непрерывна (n+1) раз на [a,b]; сущесвтует на [a,b], что

f(x) – Ln(x) =( f⁽ⁿ⁺¹⁾((n+1)!) *_n+1(x)

(кому нужно) Рассмотрим функцию (x)=f(x)L_n(x)K _n+1(x) (4) где K - некоторая постоянная, _n+1(x)= (xx₀) (xx₁)(xx_n). Пусть z  [a,b] - точка, в которой мы хотим получить оценку остаточного члена. Естественно предположить, что zx_i,   i=1,,n. Выберем K из условия (z)=0. Это значение постоянной K можно выразить через производную порядка n функции f. По построению (x_i)=0,   i=1,,n. Поэтому на отрезке [a,b] функция  обращается в нуль n+1 раз. По теореме Ролля ее первая производная должна обращаться в нуль на [a,b] хотя бы в n точках, а соответственно ⁽ⁿ⁾ - хотя бы в одной точке. Пусть это будет точка . Имеем ⁽ⁿ⁾() = f⁽ⁿ⁾() 0K n! Отсюда следует, что K  = f⁽ⁿ⁾()/ n!. Из (4), учитывая, что (z)=0, будем иметь Требуемая оценка получена.

Max| _n+1(x )| на [-1;1] - будет наименьшей, если в качестве узлов интерполяции взять корни многочлена Чебышева:

Tn(x) = cos(n*arcos(x)), |x|<=1