3.3. Правило знаков

Прежде, чем перейти к рассмотрению хода лучей через оптическую систему и выводу формул, связывающих отдельные оптические параметры, необходимо установить некоторое правило знаков, соответствующие тому или иному расположению отрезков, определяющее некоторые оптические величины:

1. Оптические системы на схемах и чертежах располагаются таким образом, чтобы расположение световых лучей происходило от источника света слева направо.

2. Если направление отрезка, расположенного вдоль оптической оси совпадает с направлением распространения света, то отрезок считается положительным, в противном случае – отрицательным. Начало отсчета отрезков должно оговариваться, однако имеются поверхности (точки), которые считаются предпочтительными. Это, во-первых – поверхности оптических деталей, во-вторых – главные и узловые точки (главные плоскости), и в-третьих – фокусы (фокальные плоскости) оптической системы (рис. 3.3.1 а).

3. Высоты, отсекаемые лучами на поверхности оптических деталей, отрезки, изображающие величину предмета или изображения предмета считаются положительными, если они распложены выше оптической оси, и отрицательными – если ниже оптической оси (рис. 3.3.1 б).

4. Углы, образованные лучами света с оптической осью или нормалью к поверхности оптической детали принимаются положительными, если ось (нормаль) нужно поворачивать до совпадения с лучом по часовой стрелке, и отрицательной в противном случае (рис. 3.3.1 в).

5. Радиусы кривизны поверхностей оптических деталей положительны, если центр кривизны расположен справа от поверхности и отрицательны – если слева (рис. 3.3.1 г).

6. Толщины оптических деталей, расстояния между ними всегда положительны (рис. 3.3.1 д).

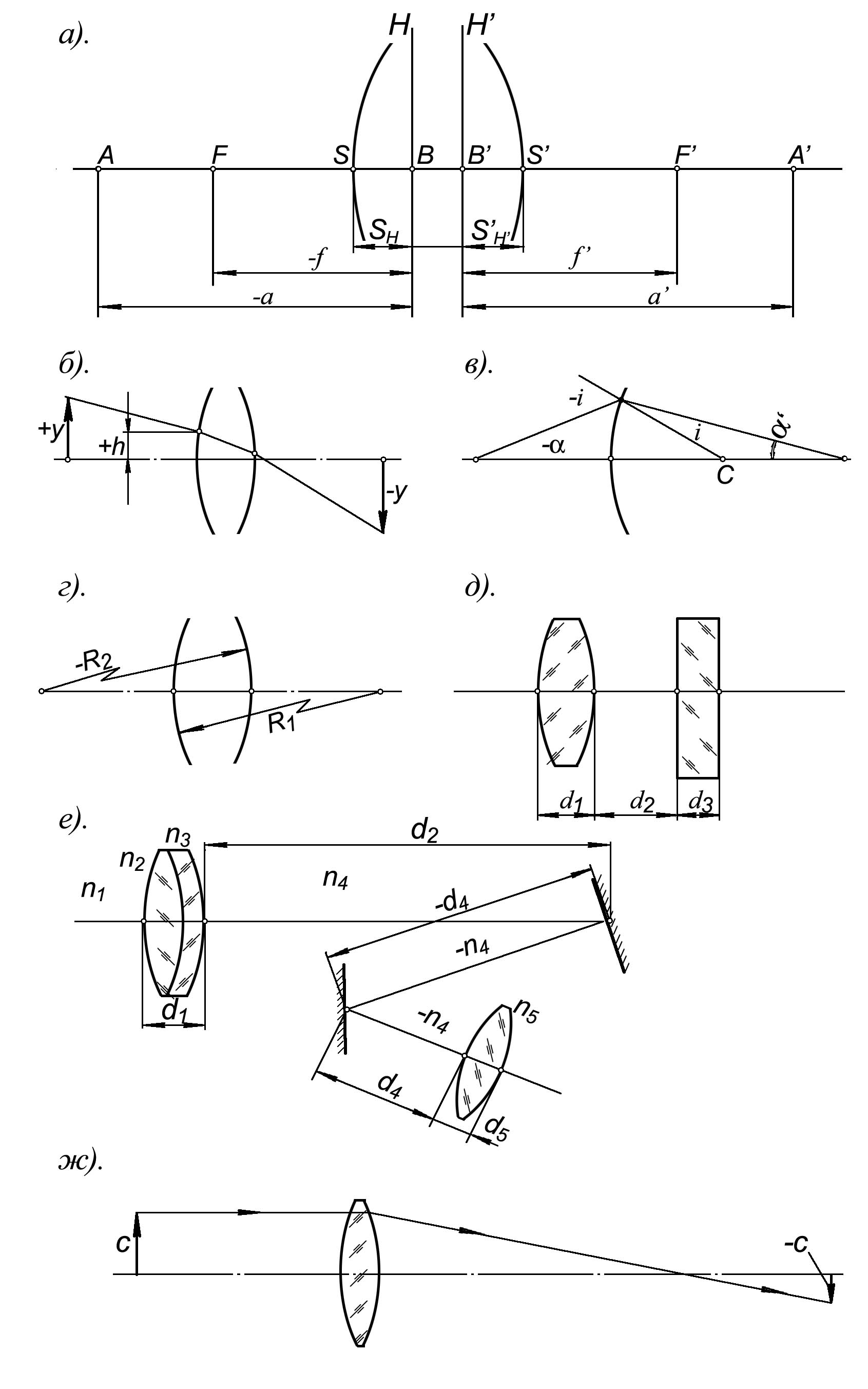
Рис. 3.3.1

7. Если в оптической системе имеются отражающие (зеркальные) оптические детали, то при использовании общих формул геометрической оптики необходимо, во-первых изменить знак у показателя преломления оптической среды после отражения и, во-вторых, изменить знак у расстояния между отражающей поверхностью и последующей оптической (рис. 3.3.1 е).

8. Увеличение оптической системы считается положительным – если величина отрезков, изображающих предмет и его изображение имеют одинаковые знаки, при противоположных знаках увеличение отрицательно (рис. 3.3.1 ж).

3.4. Основные оптические формулы. Построение изображения

На рис. 3.4.1 даны кардинальные точки – главные точки B, B’; фокусы F, F’ - оптической системы. Требуется построить изображение предмета AP=y .

Рис. 3.4.1

Для нахождения изображения точки P проследим ход двух лучей. Один луч направим параллельно оптической оси (PD₁), сопряженный луч пройдет через задний фокус F’ системы и через точку D’₁ . Второй луч проведем через передний фокус F системы. Сопряженный луч в пространстве изображений идет параллельно оптической оси. Построенные в пространстве изображений лучи D’₁P’ и D’₂P’ пересекаются в точке P’ , которая и является изображением точки P .

Пользуясь подобием одинаково заштрихованных треугольников FAP и FBD₂ ; A’P’F’ и F’D’₁B’ , найдем:

, .

Это две расчетные формулы для линейного увеличения. Приравнивая правые части формул, получим формулу, известную под названием – формула Ньютона:

Введем отрезки s=BA и s’=B’A’ . По рисунку видим

,

Подставляя в формулу Ньютона, получим

;

Деля на s^.s’ , найдем формулу отрезков:

,

при f’=-f (система находится в однородной среде):

.

Из фомул:

; ; (ф.Ньютона)

имеем:

Из формулы Ньютона:

Таким образом

Это выражение позволяет получить формулу для линейного увеличения через отрезки s и s’

;

При f’=-f формула приобретает простой вид

Рассмотрим графическое построение изображения. При построении изображения мы исходим из свойств лучей, проходящих через кардинальные точки системы. Проследив ход двух лучей, исходящих из какой-либо точки предмета, и прошедших через оптическую систему, мы находим их точку пересечения в пространстве изображений, которая и будет искомым изображением точки предмета. Следует иметь в виду, что пространство предметов не обязательно находится слева от системы, а пространство изображений – справа: они могут находится с любой стороны.

Рис. 3.4.2

Рис. 3.4.3

;

;

По формуле Ньютона:

;

Тогда

и

Обозначив линейное увеличение в точках A₁ A’₁ через V₁, а в точках A₂ A’₂ через V₂, можно записать:

В случае, когда точка A₂ неограниченно приближается к точке A₁ , то x₂  x₁ и V₂  V₁ . В пределе, когда точка A₂ совпадает с точкой A₁ , продольное увеличение Q переходит в продольное увеличение в точках, обозначаемое через q ,

Если f’ = f , то q = V² .

Мы знаем, что угловое увеличение (рис. 3.4.4).

Рис. 3.4.4

;

Тогда

Но

;

Тогда ;

, то есть

линейное увеличение равно произведению углового увеличения на продольное.