3.2. Линейное и угловое увеличение оптической системы.

Кардинальные точки

Линейным увеличением оптической системы - называется отношение величины изображения предмета к величине самого предмета:

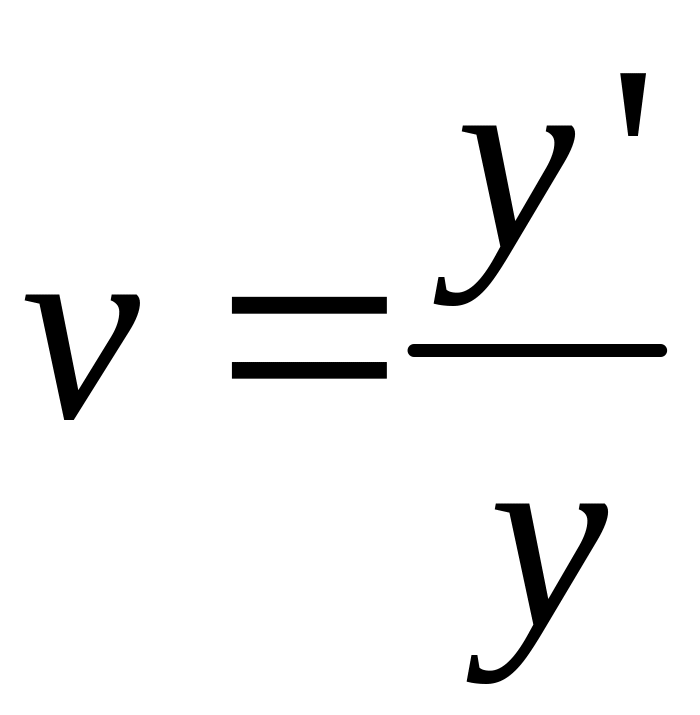
Для данной пары сопряженных, перпендикулярных к оптической оси плоскосей (рис. 3.2.1), линейное увеличение есть величина постоянная, не зависящая от величины предмета y.

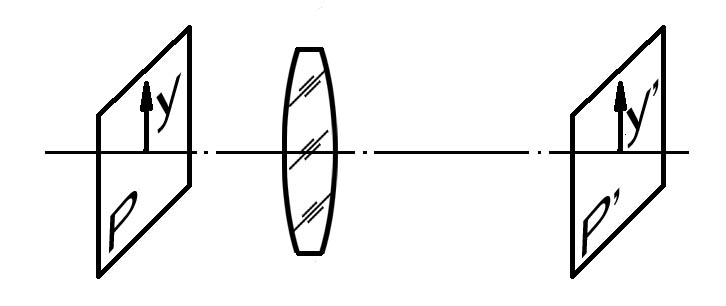
Рис. 3.2.1

Угловым увеличением называют отношение тангенсов угла наклона луча к оптической оси в пространстве изображений к тангенсу угла наклона луча в пространстве предметов (рис. 3.2.2):

Или для малых углов:

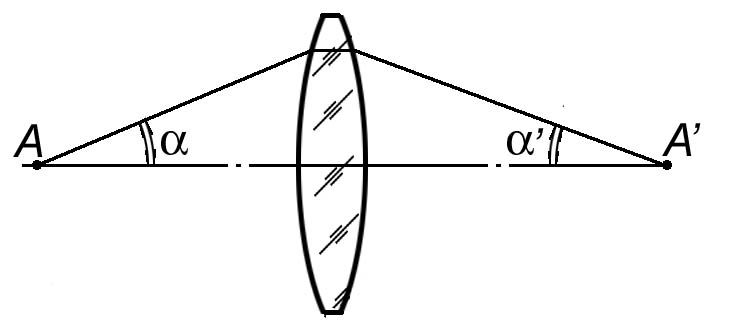
Рис. 3.2.2

Оптическая система имеет ряд кардинальных точек, определяющих основные ее свойства. Любую оптическую систему, представленную в нашем случае двумя сферическими поверхностями, можно характеризовать способностью собирать лучи в одной точке. Если лучи идут параллельно оптической оси из пространства предметов (рис. 3.2.3 а) то они соберутся в точке F’, называемой задним фокусом оптической системы. Плоскость, перпендикулярная оптической оси и проходящая через задний фокус, называется задней фокальной плоскостью. Пучок лучей, проходящий оптическую систему под некоторым углом к оптической оси, также собирается в фокальной плоскости, но на некотором расстоянии от оптической оси. Таким образом, можно сказать, что задняя фокальная плоскость есть плоскость изображения бесконечно удаленной плоскости, расположенной в пространстве предметов. Всякая точка плоскости, расположенной в бесконечности в пространстве предметом изображается точкой, расположенной в задней фокальной плоскости.

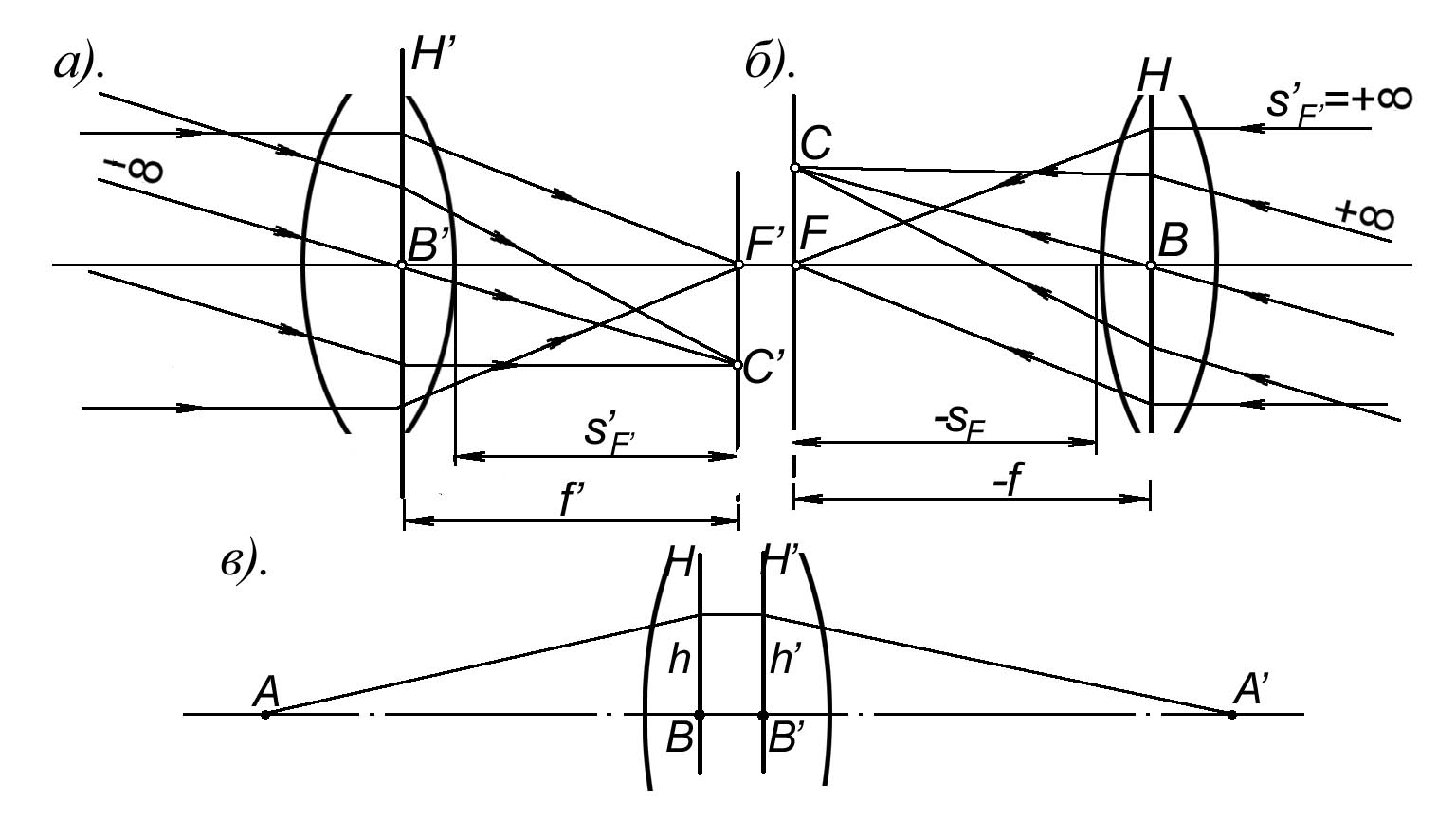
Рис. 3.2.3

Абсолютно то же самое можно сказать относительно лучей, проходящих систему справа налево (рис. 3.2.3 б). Разница заключается лишь в том, что точка F называется передним фокусом, плоскость, проходящая через точку F перпендикулярно оптической оси – передней фокальной плоскостью.

В следствии обратимости хода лучей через оптическую систему, всякий пучок лучей, исходящий из точек, расположенных на фокальных плоскостях (передней или задней) после прохождения системы будет идти параллельным пучком. Если пучок лучей исходит из точки F (или F’), то пучок лучей после системы будет параллелен оптической оси.

Если мы теперь продолжим до пересечения входящий в систему и выходящий луч (рис. 3.2.3 а), то практически мы можем отобразить преломляющие сферические поверхности и считать, что изменение направления луча происходит в точке, находящейся на плоскости H’. То же самое можно проделать и с лучами, идущими из пространства предметов (рис. 3.2.3 б).

Плоскости H и H’ - называются главными плоскостями оптической системы, линейное увеличение в этих плоскостях равно +1 (рис. 3.2.3 в). Точки пересечения этих главных плоскостей с оптической осью называются главными точками: ( B и B’).

Главные точки B и B’ являются второй парой кардинальных точек оптической системы. Причем, плоскость H и точка B называются передней главной плоскостью и передней главной точкой системы, а плоскость H’ и точка B’ - соответственно задней главной плоскостью и задней главной точкой.

Расстояние от передней главной плоскости до переднего фокуса называется передним фокусным расстоянием, от задней главной плоскости до заднего фокуса – задним фокусным расстоянием.

Расстояние от вершины последней поверхности оптической системы до заднего фокуса и от вершины первой поверхности до переднего фокуса называется соответственно задним или передним вершинным фокусным расстоянием ( ).

Оптические системы или линзы по своему действию на пучок лучей разделяются на собирающие (или положительные) и рассеивающие (или отрицательные). Если параллельный пучок лучей, падающий на линзу собирается в точке, расположенной справа от линзы (рис. 3.2.4 а), то линза (система) называется положительной ’ > 0 ; если же точка схода лучей расположена слева от линзы, то линза называется отрицательной (рис. 3.2.4 б) ’ < 0.

Рис. 3.2.4

Третья пара кординальных точек – узловые точки. Узловыми точками называются такие точки, угловое увеличение в которых равно +1, то есть (рис. 3.2.5):

Рис. 3.2.5

Для систем находящихся в однородной среде, узловые точки совпадают с главными. Для глаза человека или объектива фотоаппарата для подводной съемки такого совпадения нет.