- •Глава 1. Теоретические основы прикладной оптики
- •1.1. Природа света. Волновой и квантовый характер световых явлений
- •1.2. Законы распространения света
- •1.3. Способы определения скорости света
- •1.4. Когерентность [7]
- •1.4.1. Степень когерентности светового пучка
- •1.4.2. Методы измерения пространственной и временной когерентности
- •1.5. Дисперсия света
- •1.6. Интерференция света
- •1.7. Интерференционные линии равной толщины и равного наклона
- •1.8. Интерферометры
- •1.8.1. Интерферометр Линника
- •1.8.2. Интерферометр Рэлея
- •1.8.3. Звездный интерферометр Майкельсона
- •1.8.7. Схема интерферометра Майкельсона
- •1.8.4. Интерферометр Фабри-Перо
- •1.8.5. Интерферометр Жамена
- •1.8.6. Интерферометр Рождественского
- •1.8.7. Использование интерференции света в промышленности
- •1.9. Дифракция света. Принцип Гюйгенса Френеля
- •1.10. Дифракция Фраунгофера
- •1.10.1. Дифракция от щели
- •1.10.2. Дифракционная решетка
- •1.10.3. Дифракционная решетка как спектральный прибор
- •1.11. Дифракция на круглом отверстии
- •1.11.1. Зоны Френеля
- •1.11.2. Зонная пластинка
- •1.11.3. Линза как дифракционный прибор
- •1.11.4. Пятно Пуассона
- •1.12. Поляризация света
- •1.12.1. Свет поляризованный и неполяризованный. Закон Малюса
- •1.12.2. Одноосные кристаллы
- •1.12.3. Скрещенные поляризаторы
- •1.12.4. Двойное лучепреломление
- •1.12.5. Поляризаторы
- •1.12.6. Анализ поляризованного света
- •1.12.7. Естественное вращение плоскости поляризации
- •1.12.8. Эффект Зеемана и поляризация
- •1.12.9. Искусственное двойное лучепреломление
- •1.12.10. Магнитное вращение плоскости поляризации
- •1.13. Оптически бесцветное стекло. Марки стекла
- •1.14. Требования к стеклу. Классы и категория стекла
- •1.15. Цветное оптическое стекло. Техническое стекло
- •1.16. Выполнение рабочих чертежей оптических деталей в соответствии с ескд
- •Глава 2. Основные оптические детали
- •2.1. Зеркала
- •2.2. Тонкие линзы
- •2.3. Плоскопараллельная пластинка
- •2.4. Оптический клин
- •2.5. Отражательные призмы
- •2.6. Развертка призм в плоскопараллельную пластинку
- •Для прямоугольной призмы с двумя отражениями
- •2.7. Редуцирование призм. Графоаналитический метод расчета призм
- •2.8. Компенсаторы
- •Глава 3. Основные свойства идеальной оптической системы
- •3.1. Идеальная оптическая система
- •3.2. Линейное и угловое увеличение оптической системы.
- •3.3. Правило знаков
- •3.4. Основные оптические формулы. Построение изображения
- •3.5. Инвариант Аббе
- •3.6. Расчет хода нулевого луча
- •3.7. Отдельная линза в воздухе
- •3.8. Расчет хода нулевого луча через сложную оптическую систему
- •3.9. Оптическая система из двух компонент
- •Положим и выберем произвольно, тогда из формул
- •3.10. Графический способ определения хода нулевого луча
- •3.11. Определение хода действительного луча
- •Глава IV. Общие свойства оптических систем
- •4.1. Основные характеристики оптического прибора
- •4.2. Видимое увеличение
- •4.3. Основные фотометрические понятия
- •4.4. Потери света
- •4.5. Диафрагмы и их значение
- •4.6. Виньетирование
- •4.7. Светосила
- •4.8. Освещенность по полю изображения
- •4.9. Поле зрения
- •4.10. Глубина изображаемого пространства
- •4.11. Глубина резкости
- •4.12. Аберрации оптических систем
- •4.12.1. Классификация аберраций
- •4.12.2. Хроматическая аберрация
- •4.12.3. Сферическая аберрация
- •4.12.4. Астигматизм и кривизна изображения
- •4.12.5. Кома
- •Величина, численно характеризующая кому, равна
- •4.12.6. Дисторсия
- •Глава 5. Теория оптических приборов
- •5.1. Зрачки и люки
- •5.2. Отрезки, определяющие положение зрачков
- •5.3. Передача перспективы оптическими приборами
- •5.4. Основные фотометрические величины
- •Мы имеем
- •5.5. Источники излучения
- •5.6. Приемники световой энергии
- •5.7. Светосила оптического прибора
- •5.8. Светосила оптического прибора с малой передней апертурой и малой задней апертурой
- •5.9. Потери света в оптическом приборе
- •Преобразуем эту формулу
- •5.10. Глаз человека
- •5.11. Видимое увеличение оптического прибора
- •5.12. Глубина резкости фотографического аппарата, лупы и микроскопа
- •5.13. Критерий разрешающей способности оптического прибора
- •5.14. Разрешающая способность зрительных труб и фотографических объективов
- •Глава 6. Теория микроскопа
- •6.1. Оптическая система микроскопа
- •Из формулы
- •6.2. Формулы геометрической теории микроскопа
- •Поэтому
- •6.3. Осветительная система микроскопа
- •6.4. Основы дифракционной теории микроскопа
- •6.5. Разрешающая способность микроскопа
- •Окуляр, в нашем случае, есть лупа, для которой мы имели формулу
- •6.6. Фазовый контраст
- •6.7. Производство современных микроскопов
- •6.7.1. Световые
- •Микроскопы серии dm lm
- •Глава 7. Теория телескопических систем
- •7.1. Телескопические системы
- •Для продольного увеличения была получена формула
- •7.2. Зрительная труба Галилея
- •7.3. Зрительная труба Кеплера
- •7.4. Окуляры и объективы зрительных труб
- •7.5. Зрительные трубы с призменными оборачивающими системами
- •7.6. Зрительные трубы с линзовыми оборачивающими системами
- •7.7. Телескопические системы со скачкообразной переменной увеличения
- •Глава 8. Методы компьютерной оптики
- •8.1. Задачи компьютерной оптики [1,2]
- •8.2. Цифровая голография [3-5]
- •8.2.1. Общая процедура изготовления синтезированной голограммы
- •8.2.2. Получение цифровой голограммы Фурье и ее бинаризация
- •8.2.3. Киноформ
- •8.3. Фазовая проблема в оптике. Cоздание на основе решения обратных задач нового класса оптических элементов [1, 2, 6-9]
- •8.3.1. Извлечение фазовой информации из данных об интенсивности
- •8.3.2. Особенности расчета характеристик фокусаторов и корректоров излучения
- •8.3.3. Дифракционные оптические элементы
- •8.3.4. Создание фокусаторов на основе управляемых зеркал
- •8.4. Фокусировка излучения при наличии случайных помех. Использование методов адаптивной оптики [7-9]
- •8.5. Оптические элементы для анализа и формирования поперечного состава излучения [1]
- •8.6. Цифровая обработка полей в оптических системах [10-13]
- •8.6.1. Виды обработки оптических полей
- •8.6.2. Автоматизированная измерительная система для диагностики структуры лазерных пучков
- •Глава 9. Запись и обработка оптической информации
- •9.1. Общая характеристика оптических систем [1-3]
- •9.2. Однолинзовая система [1-4]
- •9.2.1. Линзы как элементы, выполняющие преобразование Фурье
- •9.2.2. Формирование изображения [1]
- •9.3. Получение изображений в сложных системах [1, 8]
- •9.3.1. Дифракционно-ограниченные системы
- •9.4. Учет аберраций [5]
- •9.5. Голографическая запись информации [2, 6-9]
- •9.5.1. Принцип голографической записи
- •9.5.2. Голограммы Фурье
- •9.6. Оптическая фильтрация и распознавание образов [2,3]
- •9.6.1. Применение системы 4-f
- •9.6.2. Голографический метод синтезирования пространственных фильтров и проблема апостериорной обработки информации
- •9.7. Сопоставление методов когерентной и некогерентной оптики [2]
- •9.8. Характеристики качества изображения [10]
- •Оглавление
Глава 2. Основные оптические детали
2.1. Зеркала
Ранее были рассмотрены законы отражения и преломления света, которые являются основными в геометрической оптике.
З акон
отражения.
(рис. 2.1.1). Луч, падающий и луч отраженный
лежат в одной плоскости с перпендикуляром,
восстановленном в точке падения луча,
при этом угол падения равен углу падения.
акон
отражения.
(рис. 2.1.1). Луч, падающий и луч отраженный
лежат в одной плоскости с перпендикуляром,
восстановленном в точке падения луча,
при этом угол падения равен углу падения.
Рис. 2.1.1
Закон преломления. (рис. 2.1.2). Луч, падающий и луч преломленный лежат в одной плоскости с перпендикуляром, восстановленном в точке падения луча, причем выполняется соотношение:
![]()

Рис. 2.1.2
Если луч идет из среды более плотной в среду менее плотную (n>n’), то преломленный луч отделяется от перпендикуляра (рис. 2.1.3) и в пределе угол преломления равен 90О. Соответствующий ему угол падения называется предельным углом полного внутреннего отражения.
![]()
![]()
Е сли
n’=1
(воздух), то
сли
n’=1
(воздух), то
![]() .
Лучи, падение на поверхность раздела
двух сред
под углом большим, чем iж
, полностью отражаются.
.
Лучи, падение на поверхность раздела
двух сред
под углом большим, чем iж
, полностью отражаются.
Рис. 2.1.3
С явлением, которое называется полным внутренним отражением, часто приходится встречаться в призмах. Если угол падения луча на отражающую меньше предельного угла полного внутреннего отражения, то такая грань призмы должна быть посеребрена, что исключает возможность преломления на этой поверхности. Углы полного внутреннего отражения для некоторых стекол:
К8 (nD =1.5163), iж = 41О15’48”,
БК10 (nD =1.3688), iж = 39О36’01”.
Плоское зеркало служит для изменения направления хода лучей. В отличие от других оптических деталей, плоское зеркало дает идеальное изображение, то есть не нарушает гомоцентричности хода лучей.
П ри
построении изображений в плоском зеркале
точки предмета и изображения лежат на
общей нормали к плоскости зеркала на
одинаковых расстояниях от него
(рис.2.1.4). От действительного предмета
(точка А) плоское зеркало дает мнимое
изображение (точка А'), то есть изображение,
расположенное за зеркалом.
ри
построении изображений в плоском зеркале
точки предмета и изображения лежат на
общей нормали к плоскости зеркала на
одинаковых расстояниях от него
(рис.2.1.4). От действительного предмета
(точка А) плоское зеркало дает мнимое
изображение (точка А'), то есть изображение,
расположенное за зеркалом.
Рис. 2.1.4
При повороте плоского зеркала вокруг точки на угол . отраженный луч отклоняется в направлении вращения зеркала на угол , равный удвоенному углу поворота зеркала, то есть = 2 (рис.2.1.5).
Р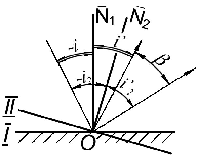 ис.2.1.5
ис.2.1.5
Д ва
зеркала, расположенные под углом
друг к другу, отклоняют падающий луч
от своего первоначального направления
на угол
= 2
, то есть угол отклонения луча не зависит
от угла падения луча на зеркало (рис.29).
ва
зеркала, расположенные под углом
друг к другу, отклоняют падающий луч
от своего первоначального направления
на угол
= 2
, то есть угол отклонения луча не зависит
от угла падения луча на зеркало (рис.29).
Рис. 2.1.6
Действительно: из треугольника ABC , – внешний угол треугольника
![]()
Из треугольника BOC ,
![]() ,
следовательно:
,
следовательно:
![]()
Эта замечательная способность двух зеркал широко используется в оптических приборах. Действительно, при повороте даух зеркал вокруг ребра O, изображение остается неподвижным, что значительно упрощает юстировку оптических приборов.
Плоские зеркала разделяются на две группы:
а). плоские зеркала с наружным слоем,
б). плоские зеркала с внутренним отражением (стеклянная пластинка, посеребренная с внутренней стороны).
Зеркала с внутренним отражением в оптических приборах стараются не применять, так как, во-первых, при прохождении оптического луча через толщу стекла возникает аберрация, и; во-вторых появляются многократные изображения одного и того же предмета в результате многократных отражений лучей внутри пластинки (рис. 2.1.7).
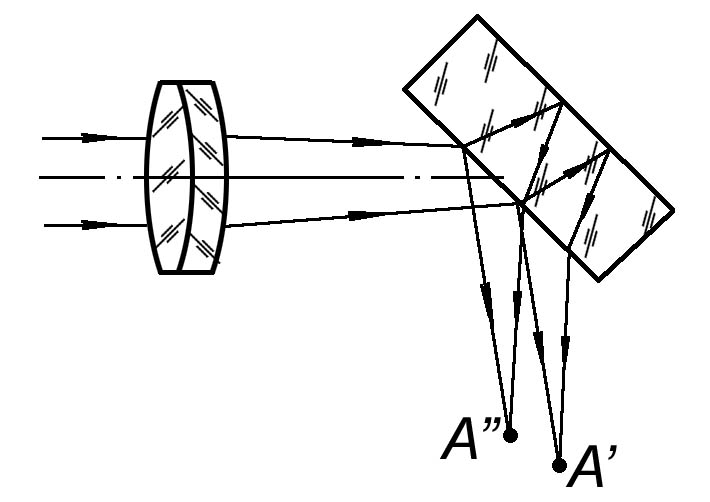
Рис. 2.1.7
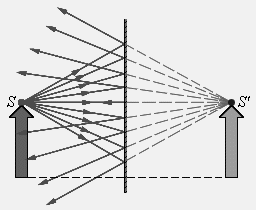
Простейшим оптическим устройством, способным создавать изображение предмета, является плоское зеркало. Изображение предмета, даваемое плоским зеркалом, формируется за счет лучей, отраженных от зеркальной поверхности. Это изображение является мнимым, так как оно образуется пересечением не самих отраженных лучей, а их продолжений в «зазеркалье» (рис. 2.1.8).
|
Рис. 2.1.8. Ход лучей при отражении от плоского зеркала. Точка S' является мнимым изображением точки S
Вследствие закона отражения света мнимое изображение предмета располагается симметрично относительно зеркальной поверхности. Размер изображения равен размеру самого предмета.
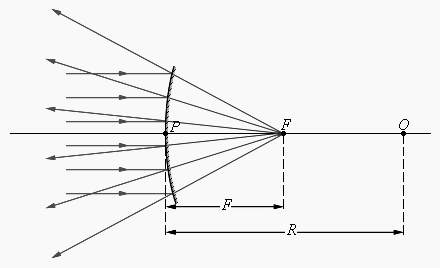
Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента. Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом. Прямая, проходящая через оптический центр и полюс зеркала, называется главной оптической осью сферического зеркала. Главная оптическая ось выделена из всех других прямых, проходящих через оптический центр, только тем, что она является осью симметрии зеркала.
Сферические зеркала бывают вогнутыми и выпуклыми. Если на вогнутое сферическое зеркало падает пучок лучей, параллельный главной оптической оси, то после отражения от зеркала лучи пересекутся в точке, которая называется главным фокусом зеркала F. Расстояние от фокуса до полюса зеркала называют фокусным расстоянием и обозначают той же буквой F. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала (рис. 2.1.9).
|
Рис. 2.1.9. Отражение параллельного пучка лучей от вогнутого сферического зеркала. Точки O – оптический центр, P – полюс, F – главный фокус зеркала; OP – главная оптическая ось, R – радиус кривизны зеркала.
Следует иметь в виду, что отраженные лучи пересекаются приблизительно в одной точке только в том случае, если падающий параллельный пучок был достаточно узким (так называемый параксиальный пучок).
Главный фокус выпуклого зеркала является мнимым. Если на выпуклое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения в фокусе пересекутся не сами лучи, а их продолжения (рис 2.1.10).
|
Рис. 2.1.10. Отражение параллельного пучка лучей от выпуклого зеркала. F – мнимый фокус зеркала, O – оптический центр; OP – главная оптическая ось.
Фокусным
расстояниям сферических зеркал
приписывается определенный знак: для
вогнутого зеркала
![]() для
выпуклого
для
выпуклого
 где
R
– радиус кривизны зеркала.
где
R
– радиус кривизны зеркала.
Изображение какой-либо точки A предмета в сферическом зеркале можно построить с помощью любой пары стандартных лучей:
луч AOC, проходящий через оптический центр зеркала; отраженный луч COA идет по той же прямой;
луч AFD, идущий через фокус зеркала; отраженный луч идет параллельно главной оптической оси;
луч AP, падающий на зеркало в его полюсе; отраженный луч симметричен с падающим относительно главной оптической оси.
луч AE, параллельный главной оптической оси; отраженный луч EFA1 проходит через фокус зеркала.
На рис 2.1.11 перечисленные выше стандартные лучи изображены для случая вогнутого зеркала. Все эти лучи проходят через точку A', которая является изображением точки A. Все остальные отраженные лучи также проходят через точку A'. Ход лучей, при котором все лучи, вышедшие из одной точки, собираются в другой точке, называется стигматическим. Отрезок A'B' является изображением предмета AB. Аналогичны построения для случая выпуклого зеркала.
|
Рис. 2.1.11. Построение изображения в вогнутом сферическом зеркале
Положение изображения и его размер можно также определить с помощью формулы сферического зеркала:
|
|
|
Здесь d – расстояние от предмета до зеркала, f – расстояние от зеркала до изображения. Величины d и f подчиняются определенному правилу знаков:
d > 0 и f > 0 – для действительных предметов и изображений; d < 0 и f < 0 – для мнимых предметов и изображений.
Для случая, изображенного на рис 3.2.4, имеем:
F > 0 (зеркало вогнутое); d = 3F > 0 (действительный предмет).
По
формуле сферического зеркала получаем:
 следовательно,
изображение действительное.
следовательно,
изображение действительное.
Если бы на месте вогнутого зеркала стояло выпуклое зеркало с тем же по модулю фокусным расстоянием, мы получили бы следующий результат:
F < 0,
d = –3F > 0,
 –
изображение мнимое.
–
изображение мнимое.
Линейное увеличение сферического зеркала Γ определяется как отношение линейных размеров изображения h' и предмета h.
Величине h' удобно приписывать определенный знак в зависимости от того, является изображение прямым (h' > 0) или перевернутым (h' < 0). Величина h всегда считается положительной. При таком определении линейное увеличение сферического зеркала выражается формулой, которую можно легко получить из рис 2.1.11:
|
|
|
В
первом из рассмотренных выше примеров
 –
следовательно, изображение перевернутое,
уменьшенное в 2 раза. Во втором примере
–
следовательно, изображение перевернутое,
уменьшенное в 2 раза. Во втором примере
 –
изображение прямое, уменьшенное в 4
раза.
–
изображение прямое, уменьшенное в 4
раза.
|
Рис. 2.1.12. Модель. Плоское зеркало |
|
Рис. 2.1.13. Модель. Сферическое зеркало |
Изображение предмета в плоском зеркале формируется за счет лучей, отраженных от зеркальной поверхности. Предмет и его мнимое изображение располагаются симметрично относительно зеркала, размер изображения равен размеру предмета.
Компьютерная модель иллюстрирует ход лучей в плоском зеркале. Обратите внимание, что если предмет располагается перпендикулярно к зеркалу, то его мнимое изображение оказывается перевернутым. Если бы предмет располагался параллельно зеркальной поверхности, то его мнимое изображение оказалось бы прямым.
Модель позволяет изменять положение предмета относительно зеркала либо с помощью соответствующих контролов, либо непосредственно с помощью мыши.
Сферическим зеркалом называют зеркально отражающую поверхность, имеющую форму сферического сегмента. Центр сферы, из которой вырезан сегмент, называют оптическим центром зеркала. Вершину сферического сегмента называют полюсом зеркала. Прямая, проходящая через оптической центр и полюс зеркала, называется главной оптической осью сферического зеркала. Точка пересечения пучка лучей, параллельных главной оптической оси и отразившихся от поверхности сферического зеркала, называется главным фокусом зеркала. У вогнутого сферического зеркала главный фокус действительный. Он расположен посередине между центром и полюсом зеркала. Главный фокус выпуклого зеркала является мнимым. Фокусным расстояниям сферических зеркал приписывают определенные знаки: для вогнутого зеркала F > 0, для выпуклого F < 0. В обоих случаях фокусное расстояние сферического зеркала равно по модулю половине радиуса кривизны зеркала |F| = R / 2. Величина, обратная фокусному расстоянию, называется оптической силой зеркала. Оптическая сила сферических зеркал измеряется в диоптриях (м–1).
Компьютерная модель иллюстрирует ход лучей при отражении от вогнутого и выпуклого сферических зеркал и образование изображений (прямых и перевернутых, действительных и мнимых). Можно изменять оптическую силу зеркала F–1 и расстояние d от предмета до зеркала. На экране дисплея с помощью стандартных лучей строится изображение предмета, и высвечиваются значения расстояния f от зеркала до изображения и линейного увеличения Γ = –(f / d). Для прямых изображений Γ > 0, для перевернутых Γ < 0.
Положение предмета относительно зеркала, а также расположение на экране всей системы – предмета, его изображения и зеркала – можно изменять с помощью мыши.