4. Критерий оптимальности.

Теорема 1. Условие 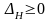(4) достаточно, а в случае невырожденности базисного плана и необходимо для его оптимальности.

Доказательство. Достаточность. Пусть выполняется условие (4). Так как , то из формулы приращения 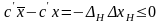или , это означает, что – оптимальный план задачи.

Необходимость. Пусть известно, что – оптимальный базисный план, причем невырожденный для задачи (1), тогда

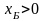(5)

Предположим противное, что условие (4) не выполняется. Следовательно, существует

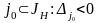(6)

По базисному плану будем строить вектор , где вектор приращения 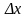выберем следующим образом.

Положим, что 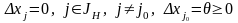(7)

Выберем 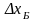, чтобы выполнялось соотношение (2), то есть

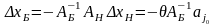(8)

Вектор 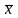в силу (2) при любом 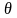удовлетворяет основным ограничениям (1): 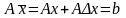. Очевидно, компоненты удовлетворяют прямым ограничениям задачи (1). Имеем

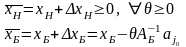
(9)

Поскольку выполняется условие (5), можно подобрать положительным, что будут выполняться прямые ограничения , тогда для найденного получаем, 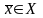является планом задачи. Но подстановка его в (3) приводит к неравенству: 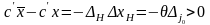. Следовательно, . Это противоречит оптимальности базисного плана , что и доказывает необходимость.

Ч.т.д.

5. Достаточное условие неограниченности. Алгоритм обратной матрицы.

Предположим, что на базисном плане не выполняется условие (4), тогда справедлива следующая теорема.

Теорема 2. Условие существования (10)

достаточно для того, чтобы .

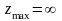Доказательство. Пусть – базисный план и выполняется условие (10). Будем строить , где вектор приращения выбираем по формулам 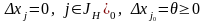(7) и 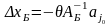(8). Тогда из (9) видно, что для .

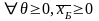Это означает, что для любого неотрицательного , будет планом и задачи (1), а из формулы приращения 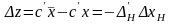(3), тогда имеем

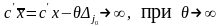(11)

то есть с ростом целевая функция будет неограниченно возрастать, оптимального плана задачи не будет и . Ч.т.д.

Выберем некоторый номер 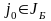и вектор ,

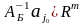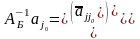
Лемма. Числа 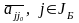являются коэффициентами разложения вектора 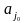по базису в 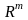составленному из векторов (его координаты в этом базисе).

Доказательство.

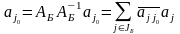(12)

Ч.т.д.

6. Итерация. Симплекс-метод (алгоритм).

Алгоритм:

При практическом использовании реализуется различные модификации симплекс метода: табличный, мультипликативный и так далее. Для реализации на ЭВМ наиболее удобна следующая:

1. Пусть дана каноническая задача со своими параметрами 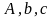и пусть известна начальная обратная базисная матрица 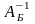(обычно 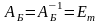и тогда ).

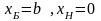2. Вычисляем начальный базисный план: из основных ограничений получаем ;

3. Строим вектор оценок базисного плана, используя (3): ;

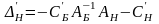4. Проверяем критерий оптимальности 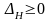(4). Если он выполняется, то записываем ответ – оптимальный базисный план, вычисляем . Если (4) не выполняется, то переходим к пункту 5;

5. Проверяем достаточное условие неограниченного роста (10): если оно выполняется, то записываем ответ (оптимального плана нет, целевая функция неограниченно растёт на ), если не выполняется, то переходим к пункту 6;

6. Совершаем итерацию:

6.1. Находим

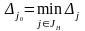
6.2. Находим

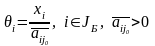
6.3. Находим

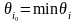
6.4. Строим по формулам:

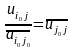
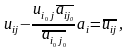
6.5. 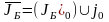. И возвращаемся в пункт 2.

В этом алгоритме основную роль играет и лишь она на итерациях пересчитывается. Табличную модификацию симплекс-метода, изучим в лабораторном практикуме.