2. Графический метод.

Метод применим к задачам линейного программирования с двумя переменными:

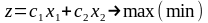(1)

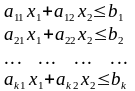(2)

Алгоритм:

1. В декартовой системе координат на плоскости строим множество планов задачи, как пересечение -полуплоскостей, задаваемых линейными ограничениями системы (2).

При этом возможен один из случаев:

а) – пустое множество;

б) – выпуклый многоугольник;

в) – выпуклая неограниченная многоугольная область.

Если а), то задача не имеет решения; б) или в) – переходим к пункту 2.

2. По целевой функции 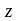строим вектор 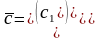(градиент целевой функции), через начало координат проводим прямую (линию нулевого уровня целевой функции): .

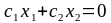3. При решении задачи максимизации (минимизации) прямую 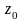перемещаем параллельно в направлении вектора 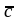(вектора - 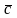) в наиболее отдалённую точку А (точку В) множества плана . Координаты точки А (точки В) и составляют оптимальный план задачи максимизации (минимизации) функции 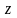на множестве .

Если множество – ограничено, то задача всегда имеет решение. Если же – неограниченная многоугольная область, то задача может не иметь решения в случае, когда не существует наиболее удалённой точки, то есть целевая функция неограниченно возрастает (убывает) на .

Если задача имеет оптимальный план, то он достигается либо в одной из вершин границы множества , либо на одной из её сторон (альтернативный оптимум).

3. Каноническая задача. Базисный план. Формула приращений

Метод разработан для канонической задачи линейного программирования

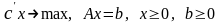(1)

Её особенность: целевая функция максимизируется; все основные ограничения имеют вид равенств; на все переменные наложены прямые ограничения неотрицательности.

Введём обозначения:

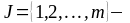индексное множество номеров переменных.

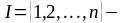индексное множество номеров основных ограничений.

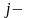ый столбец матрицы А.

Определение. Пусть дан некоторый план 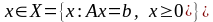. Его будем называть базисным планом, если компоненты можно разбить на две группы: базисные 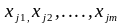или 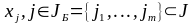и небазисные 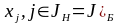и выполняются два условия:

а) небазисные компоненты плана нулевые ;

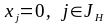б) базисным компонентам соответствуют линейно-независимые столбцы матрицы А, то есть .

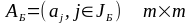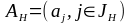
Построим матрицу . Согласно определению, она не вырождена . Эта матрица называется базисной, а матрица 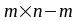называется небазисной.

Определение. Базисный план называться невырожденным, если все базисные компоненты положительны .

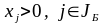Формула приращений целевой функции

Будем рассматривать задачу вида:

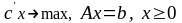(1)

Предположим, что известен базисный план 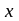, характеризующийся индексным множеством 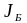. Рассмотрим произвольный другой план 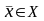и подсчитаем, как изменится целевая функция при переходе .

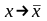Обозначим через 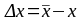– вектор приращения базисного плана, тогда по базисному множеству введем разбиение:

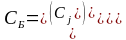
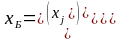
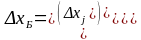
поскольку – планы задачи (1), то выполняется соотношения:

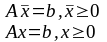
Вычитая основные ограничения, получим: 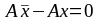или .

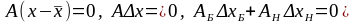Таким образом,

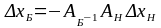(2)

Формула (2) выражает базисные компоненты вектора приращений через небазисные. И если вектор 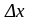удовлетворяет (2), то вектор 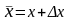будет планом задачи тогда и только тогда, когда – будет план, причём 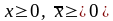. Для приращения целевой функции получим:

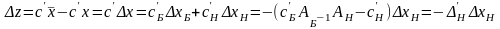(3)

где 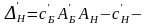вектор оценок, 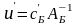– вектор потенциалов.

(3) – искомая формула приращения целевой функции при переходе от базисного плана к произвольному плану 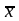. Её можно переписать

(3)