
- •Предмет курса. Основные понятия. Общая схема решения задач. Производственная задача.
- •Графический метод.
- •Каноническая задача. Базисный план. Формула приращений
- •Критерий оптимальности.
- •Достаточное условие неограниченности. Алгоритм обратной матрицы.
- •Итерация. Симплекс-метод (алгоритм).
- •Конечность. Геометрическая интерпретация.
- •Двухфазный симплекс-метод.
- •Выводы и следствия двухфазного симплекс-метода.
- •Приведение задач к канонической форме. Табличная реализация симплекс-метода.
- •Двойственная задача. Взаимодвойственность.
- •Соотношения двойственности 1,2.
Предмет курса. Основные понятия. Общая схема решения задач. Производственная задача.
Функция
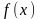 ,
заданная на множестве
,
заданная на множестве
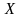 -
целевая функция, задача оптимизации в
общей форме имеет вид:
-
целевая функция, задача оптимизации в
общей форме имеет вид:
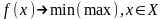 .
.
План
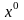 называется оптимальным, если
выполняется условие:
называется оптимальным, если
выполняется условие:
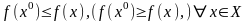 ,
где
-
оптимальный план, число
,
где
-
оптимальный план, число
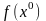 – оптимальное значение целевой функции.
– оптимальное значение целевой функции.
Предмет курса: изучение и разработка методов и алгоритмов разнообразных экстремальных задач.
При несуществовании у задачи оптимального
плана под решением может пониматься
нахождение числа (экстремального
значения целевой функции)
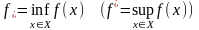 ,
и минимизирующей (максимизирующей)
последовательности планов в
,
и минимизирующей (максимизирующей)
последовательности планов в
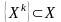 ,
обладающей свойством
,
обладающей свойством
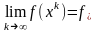 .
Если у задачи существует оптимальный
план, то минимизирующая последовательность
сходится к значениям
и
.
Если у задачи существует оптимальный
план, то минимизирующая последовательность
сходится к значениям
и
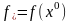 .
.
План
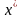 называется
называется
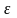 -
оптимальным, если для некоторого
положительного
(обычно малого) выполняется неравенство:
-
оптимальным, если для некоторого
положительного
(обычно малого) выполняется неравенство:
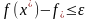
План
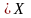 называется локально-оптимальным, если
существует
называется локально-оптимальным, если
существует
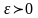 ,
что выполняется неравенство:
,
что выполняется неравенство:
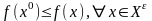 ,где
,где
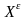 -
это
-окрестность
плана
в
-
это
-окрестность
плана
в
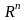 ,
,
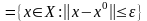 ,
то есть план
наилучший по крайней мере в своей
окрестности радиуса
.
,
то есть план
наилучший по крайней мере в своей
окрестности радиуса
.
Общая схема. Пусть существует некоторый объект поведения, который необходимо оптимизировать.
Этапы достижения цели исследования следующие:
Изучение и описательная постановка.
Он включает:
а) изучение структуры объекта, его составных частей;
б) установление связей и закономерностей его функционирования;
в) выяснение смысла качества, улучшение поведения объекта ;
г) сбор числовых данных, описывающих состояние связи и закономерности, качество поведения объекта;
Математическая формализация задачи.
Оно включает:
а) введение неизвестных управляемых
параметров для изменения поведения
объекта -
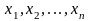 ,
которые однозначно описывают состояние
объекта, и изменяя который можно
добиваться целей;
,
которые однозначно описывают состояние
объекта, и изменяя который можно
добиваться целей;
б) запись в виде математических соотношений
основных связей и закономерности. Обычно
они имеют вид неравенств и равенств,
связывающих переменные
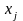 ,
,
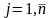 и используют собранную в 1. информацию.
Система этих соотношений и определяет
(задаёт) множество;
и используют собранную в 1. информацию.
Система этих соотношений и определяет
(задаёт) множество;
в) запись целевой функции и операции оптимизации.
В результате второго этапа мы получаем задачу оптимизации (1).
Исследование задачи и построение метода.
Оно включает:
а) выяснение, к какому типу задач оптимизации относится наша, имеет ли разработанная теория и методы решения;
б) если теория разработана и имеются методы, то изучаем теории и выбор наиболее подходящего метода;
в) если теории и методов (подходящих) нет, то исследование задачи (дополнительное) и на этой основе разработка методов.
Численное решение.
Оно включает:
а) составление на основе метода алгоритма;
б) написание и отладка по алгоритму программы на ЭВМ;
в) получение оптимального плана и оптимального значения целевой функции.
5. Анализ решения и уточнение модели и процесса оптимизации, (сравниваем полученное решение с реальным поведением объекта; если есть возможность, то проводим эксперименты; если удовлетворяет, то процесс оптимизации заканчивается, если нет, то уточняем этот процесс на этапах 1-4. при оптимизации возможны ошибки сбора информации, моделирования, исследования, вычисления).
