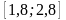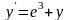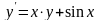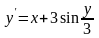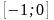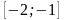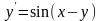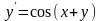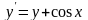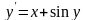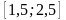Чисельне рішення звичайних диференціальних рівнянь методом Ейлера-Коши.

Необхідні відомості з теорії (див 9.1 -10.6).

1. Загальне і часткове рішення звичайного диференціального рівняння 1-го порядку. Інтегральні криві.

2. Задача Коші. Теорема Пікара.

3. Геометричний зміст правої частини диференціального рівняння, дозволеного відносно похідної.

4. Поняття чисельного рішення. Ламана Ейлера.

5. Метод Ейлера - Коші, його геометричний зміст.

6. Оцінка погрішності чисельного рішення методом подвійного перерахунку.

Завдання

Використовуючи метод Ейлера-Коші, знайдіть чисельне рішення

диференціального рівняння на відрізку 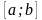з кроком 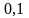, що задовольняє початковій умові 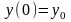(в таблицю проставляти поліпшені значення, знайдені двократними обчисленнями з кроком . Оцінити погрішності чисел методом подвійного перерахунку і визначите вірні значущі цифри цих чисел. Накреслите ламану Ейлера.

Рівняння по варіантах:

Варіант	Рівняння
1		0	0,8
2		1,8	2
3		0	1,2
4		0	2
5		1,6	2
6		0	-1
7		-1	0,5
8		-2	0
9		1	3
10		2	0
11		2	0
12		1	0
13		1	-1
14		1,5	3
15		0	0

Порядок виконання роботи

1. Переконаєтеся в існуванні і єдиності рішення поставленої задачі Коші.

2. Вичислити вручну у* і оцінити його погрішність.

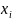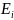3. Складіть програму виведення таблиці де у, - наближення до значення точного рішення в точці знайдене одноразовим обчисленням за методом Ейлера- Коши (з кроком h = 0,1), оцінка погрішності значення у*

4. Отримаєте шукане чисельне рішення, виписуючи табличні значення з вірними значущими цифрами.

5. Побудуйте відповідну ламану Ейлера.