9.4.2. Метод серединних точок

Геометричне виведення. Тут пошук ведеться в напрямі, характерному для інтегральних кривих в точках, абсцисами яких є середини відрізків . Спочатку за допомогою методу Ейлера відшукують проміжну (серединну) точку з координатами

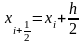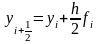, , (9.18)

Де . Потім знаходять число

, (9.19)

визначальний уточнений напрям, і беруть

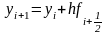. (9.20)

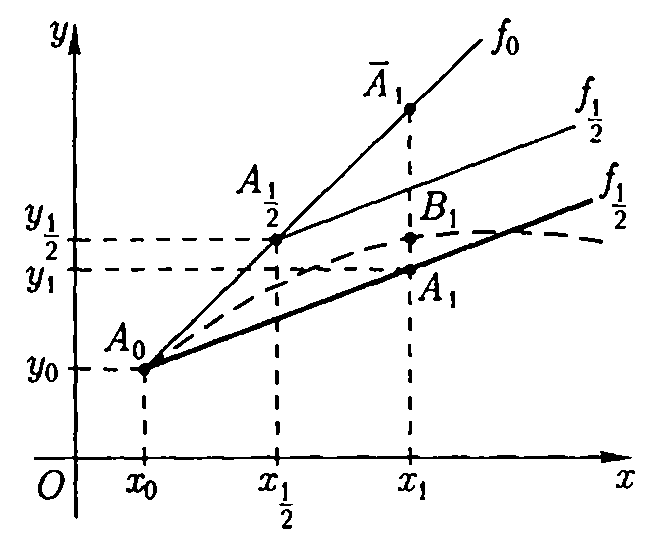
Мал. 9.5

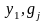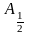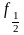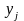Обчислення формулам (9.18) – (920) відображено на мал. 9.5. Серединною точкою тут являється . Кутовий коефіцієнт дотичної до інтегральної кривої такої, що проходить через цю точку, рівний . Формула (9.20) дає ординату точки 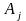_, що лежить на паралельній цієї дотичної прямої, що виходить з .

По методу Ейлера в якості отримали б ординату точки 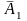. Аналітичне виведення алгоритму обчисленні методом серединних точок, так само як і у разі методу Эйлера- Коши, здійснюється за допомогою квадратичного усікання формули Тейлора.

Нехай є співвідношення (9.16). Вичислимо 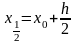та застосуємо до похідної 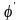теорему Лагранжа:

.

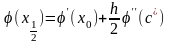
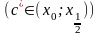Оскільки друга похідна неперервна, замінимо 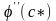на . Тоді отримаємо наближену рівність

,

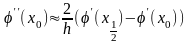праву частину якого підставимо в (9.16) замість . Після спрощень матимемо

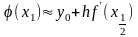(9.21)

Щоб виразити 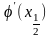приблизно через значення функції , обчислимо

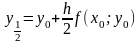
Позначивши через 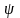рішення диференціального рівняння, що задовольняє початковій умові 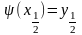, на основі тих же суджень, що були використані в попередньому пункті, отримуємо

.

Тепер в (9.21) замінимо на знайдене наближення, позначаємо праву частину через і отримаємо формулу (9.20) при .

Вправи

9.14. Виконаєте геометричні побудови, відповідні другому кроку методу серединних точок.

9.15. Виконаєте впр. 9.12 методом серединних точок.

9.16. Чим ближче до , грубе наближення 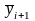в методі Ейлера-Коші, тим краще число 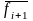відбиває напрям точної інтегральній кривій в точці з абсцисою а значить, тим точніше знайдеться .

1. Напишіть формули комбінування методів : спочатку шукається грубе наближення 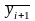методом серединних точок, а потім воно уточнюється методом Ейлера- Коши.

2. Проілюструйте графічно обчислення , по отримуваних формулам.

10.5. Точність методу Ейлера і його модифікацій

Аналіз виведення формул в 9.3 і 9.4 показує, що при побудові чисельного рішення задачі Коші нашаровуються погрішності, викликані різними джерелами. З цієї причини строгі оцінки погрішностей чисел виду 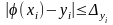виявляються складними і малопридатними (див, наприклад, [11, гл. 1]). На практиці ними не користуються, а обмежуються орієнтовочною характеристикою точності методів і знаходженням наближених значень для відстаней 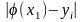за правилом Рунге. У методі Ейлера мають місце наступні основні переходи до наближених значень:

.

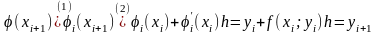Погрішність наближеної рівності (1) викликана заміною точного рішення на деяке інше рішення . Значення цієї погрішності залежить від диференціального рівняння. У одних випадках це значення може бути істотним, в інших – нехтуємо. Наближена рівність (2) обумовлена відкиданням залишкового члена формули Тейлора; що виникає при цьому погрішність усікання є основною характеристикою точності методу. Оскільки при лінійному усіканні залишковий член рівний 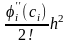, правомірний вивід: метод Ейлера при кожному переході від , до породжує погрішність, пропорційну . Говорять також, що локальна погрішність методу має порядок або рівна

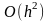(читається " велике від " ).

Ясно, що від слід чекати меншої точності, чим від . Як відзначалося в 9.2, при русі до кінця таблиці відбувається накопичення погрішностей, тому їх слід підсумовувати. Враховуючи, що довжина відрізку 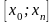рівна 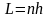, вичислимо порядок погрішності числа , знайденого після n кроків:

.

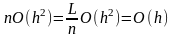Звідси слідує вивід, що глобальна погрішність методу Ейлера по усій таблиці рівна 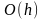. Аналогічними міркуваннями переконуємося, що локальна погрішність методу Ейлера - Коши і методу серединних точок рівна 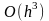, а їх глобальна погрішність - . Таким чином, ці методи на порядок точніші за метод Ейлера. Отримані характеристики досить грубі, але вони дозволяють упізнати вплив кроку таблиці на точність чисельного рішення. При зменшенні кроку h удвічі можна чекати в середньому приблизно двократного зменшення погрішностей знайдених методом Ейлеpa табличних значень якщо ж , обчислювалися по модифікованим алгоритмам, то їх точність зростає в четверо.

Зауваження. Відмітимо, що вивчені нами метод Ейлера і його модифікації належать до сімейства так званих методів Рунге - Кутта. Для чисельного вирішення задачі Коші на практиці використовується ще один метод з цього сімейства. Його локальна і глобальна точність характеризується порядками 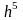і 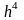відповідно. Тепер приведемо без доказу використовувані на практиці формули приблизної оцінки точності значень чисельного рішення методом подвійного перерахунку (методом Рунге). Вони засновані на обліку тільки погрішностей усікання формули Тейлора, тобто при цьому нехтують іншими джерелами погрішностей, включаючи і обчислювальні. Нехай будується таблиця з віддаленими на крок h аргументами 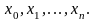Спочатку одним з методів відшукують значення , 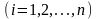з кроком h, а потім проводяться обчислення з кроком 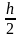. Зрозуміло, що в останньому випадку при кожному переході від даного аргументу до наступного буде потрібно двократне застосування методу. Відповідні аргументам нові табличні значення позначимо через 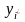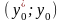. Це поліпшені наближення до 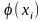, і тому таблицю з даними 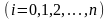візьмемо в якості шуканого чисельного рішення з кроком h.

Відстані між 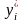і точними числами обчислюються по наближених формулах:

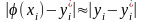(10.22)

для методу Ейлера і

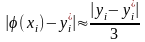(10.23)

для обох модифікацій методу Ейлера.

Приклад 10.3. Нехай чисельне рішення диференціального рівняння , що задовольняє початковій умові 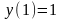, шукається методом Ейлера у вигляді таблиці з кроком 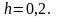Вимагається знайти та 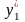, відповідні аргументу 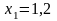і оцінити погрішність .

При отримаємо

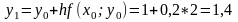
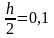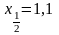Тепер проведемо двократні обчислення з кроком . Спочатку знаходимо і

.

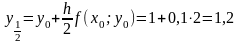Потім обчислюємо значення :

.

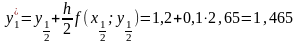За допомогою (10.22) знайдемо приблизну оцінку погрішності :

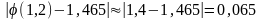
Вправи

10.17. Протягом прикладу 10.3 знайдіть значення 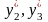для аргументів 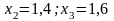та оцініть їх погрішності (при обчисленнях зберігайте три цифри після десяткової коми).

10.18. 1. Напишіть усі формули, необхідні для обчислення за початковими табличними даними з кроком обома модифікованими методами Ейлера, і відобразите на малюнку геометричний сенс обчислень.

2. Виконаєте завдання прикладу 10.3, застосовуючи замість методу Ейлера метод Ейлера- Коши.

10.19.* Виведіть наближену рівність

для коефіцієнта пропорційності погрішності лінійного усікання формули Тейлора.

Вказівка. Застосуєте ідеї, використані при виведенні формул методу Ейлера - Коши.