9.3. Метод Ейлера

Нехай вимагається знайти чисельне рішення рівняння (9.1), що задовольняє початковій умові (9.4). На додаток до угоди 9.1 вважаємо, що часні похідні та неперервні в області . Позначимо через φ точне рішення поставленої задачі Коші. Через зроблені припущення похідні другого порядку функції φ та всіх інших рішень рівняння (9.1), графіки яких проходять через використовувані в процесі подальших обчислень точки , існують і безперервні в околиці абсцис цих точок (теорема 9.2).

Чисельне рішення шукаємо у вигляді таблиці 9.2. Для цього виберемо

крок h число , вичислимо (i = 0, 1,.., n) і проставимо ці аргументи в таблицю.

Далі потрібно знайти y_t виходячи з відомих даних та . Скористаємося формулою Тейлора :

, де (9.7)

Через неперервність при малих h можна відкинути останній доданок з правої частини. Тоді, з урахуванням (9.5) і того, що отримаємо

.

Отже, можна взяти

(9.8)

Тепер відомі табличні дані та . Для виведення формули обчислення вимагається рішення, задовольняюче початковій умові при . Функція φ тут може не підійти. Позначимо через φ те рішення, для якого вірна рівність і знову скористаємося формулою Тейлора:

, де (9.9)

Відкидаємо доданок з і завдяки рівності отримуємо

.

Якщо крок h малий і рішення φ мало відрізняється від , отримане

наближення до можемо вважати наближенням і до .Тоді

.

Далі діємо аналогічно, використовуючи при пошуку по відомій точці відповідне часткове рішення .

У результаті отримаємо формули методу Ейлера

(9.11)

що дозволяють послідовно знаходити значення y_i у таблиці 9.2.

Обчислення методом Ейлера мають простій геометричний зміст (мал. 9.3). Через початкову точку штриховою лінією проведена інтегральна крива (вона може бути невідомою). Число визначить дотичну до цієї кривої в точці . Узявши на цій дотичній точку , з абсцисою , можна розглянути прямокутний трикутник з кутом α при вершині і паралельним осі Ох з катетом . Оскільки , добуток дасть довжину катета _, а формула (9.8) - ординату , точки . Прослідкуємо ще один крок обчислень. Через точку , проходить деяка інтегральна крива . Дотична до неї в цій точці має кутовий коефіцієнт . По формулі (9.10) визначається ордината точки Помічаємо, що , представляє собою наближене значення кутового коефіцієнта дотичної до точної кривої в точці . Таким чином, маючи деяку точку (спочатку це ) і провівши через неї дотичну до відповідної інтегральної кривої, можна знайти , як ординату точки цій дотичній, відповідній абсцисі . Відрізки прямих між послідовними точками утворюють ламану Ейлера.

У геометричних міркуваннях істотно використовується те, що область обчислень заповнена спорідненими інтегральними кривими з однаковою або схожою конфігурацією. Зважаючи на це при кожному число , визначає не лише напрям кривої в точці , з цією чи іншою степеню точності задає напрям інших близьких до неї кривих в точках з абсцисою , (зокрема, напрям точної інтегральної кривої). Іншими словами, з допомогою можна дізнатися характер напрямів інтегральних кривих уздовж прямої .

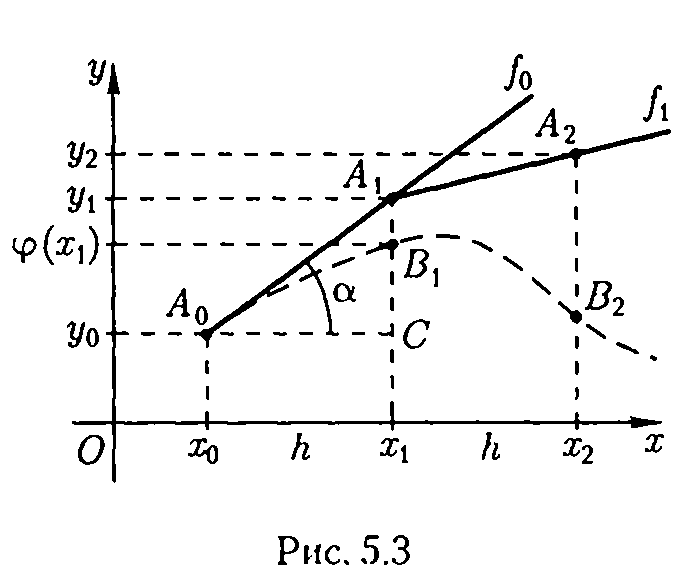
Мал. 9.3

Метод Ейлера задає простий алгоритм обчислень, але визначає табличні значення з невисокою точністю. Як видно з геометричного змісту формул, при пошуку використовуються напрями інтегральних кривих, характерні для лівого кінця відрізку , і не враховується зміна в поведінці цих кривих на усьому відрізку. На мал. 9.3 видно, що з цієї причини число виявляється дуже грубим наближенням до .

0	0	0	0
0,4	0	0,16	0,16
0,8	0,32	0,64	0,32
1,2	0,96	1,44	0,48
1,6	1,92	2,56	0,64
2,0	3,20	4,00	0,80

Табл. 9.3

Приклад 9.2. Дані рівняння та початкова умова . Знайдемо методом Ейлера чисельне рішення задачі Коші на відрізку з кроком .

Використовуючи , , знаходимо . Потім

, і так далі . В результаті отримаємо таблично задану функцію , розміщену в перших двох стовпцях таблиці. 9.3. У третьому стовпці таблиці приведені значення точного рішення φ: , а в четвертому стовпці - погрішності , чисел .

Оскільки крок h вибраний великим, погрішності великі. Помічаємо, що вони ростуть у міру наближення до кінця таблиці.

Вправи

9.8. Накресліть точну інтегральну криву з прикладу 9.2 і ламану Ейлера, відповідну отриманому там чисельному рішенню.

9.9. Дано диференціальне рівняння . Знайдіть методом Ейлера на відрізку з кроком чисельне рішення задачі Коші з початковою умовою (обчислення вести з двома цифрами після десяткової коми). Визначити погрішності , використовуючи точне рішення . Побудуйте ламану Ейлера і точну інтегральну криву.

9.10. Формули методу Ейлера можна вивести різними способами. Отримаєте формулу (9.8) :

1) замінивши точну інтегральну криву на дотичної до неї, проведеної в точці(геометричний вивід);

2) проінтегрував тотожність (9.2) по відрізку (врахуйте при цьому, що зважаючи на безперервність функцій f і φ при малих h можна взяти