Приклад 1.

Маємо ряд із результатів, який після упорядкування буде мати вигляд: 11; 12; 12; 12; 13; 13; 14; 14; 15; 18.

Як бачимо, є сумнів відносно 10-го результату . Чи є підстави для його вилучення з подальшої обробки?

Для наведених даних , а . Тоді значення . Якщо задатися рівнем значимості (тобто ймовірність відкинути гіпотезу, в разі коли вона правильна), з табл. 3.4 для знаходимо Розраховане значення і воно буде більше . Це означає, що гіпотеза про однорідність отриманих результатів відкидається і слід вилучити з подальшої обробки.

У випадку, коли у нас виникає підозра щодо мінімального результату, то для перевірки гіпотези необхідно скористатися величиною

.

В подальшому процедура перевірки відрізняється лише тим, що з порівнюється .

Розглянемо ще один критерій вилучення одного екстремального результату, запропонований Ф. Граббсом [42].

Для побудови вирішального правила при вилученні максимального результату використовується величина

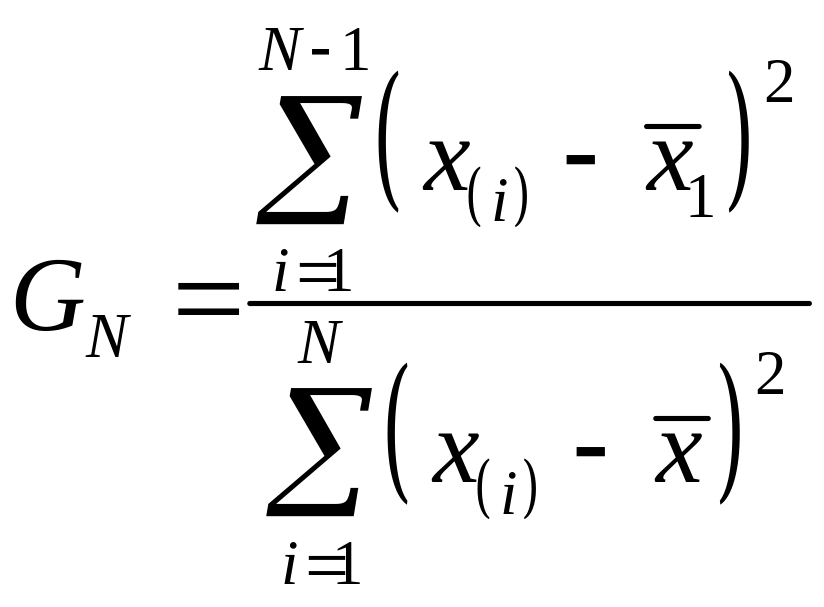, (3.23)

де , .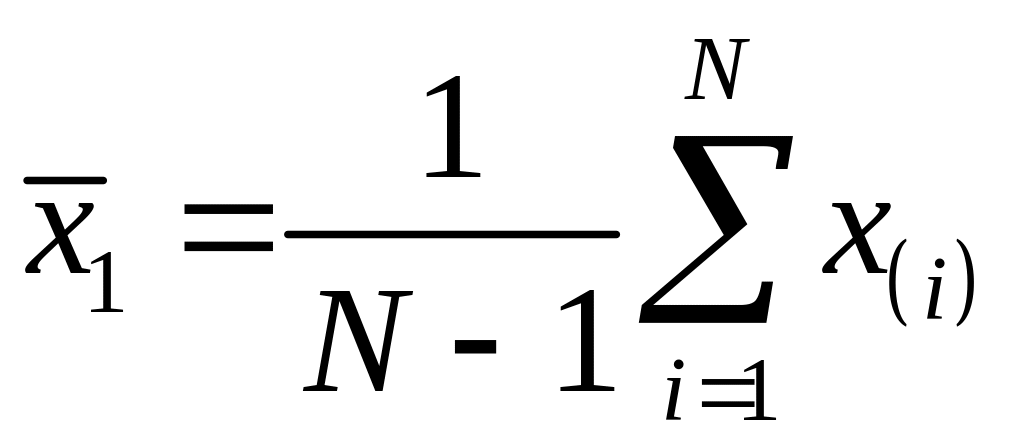

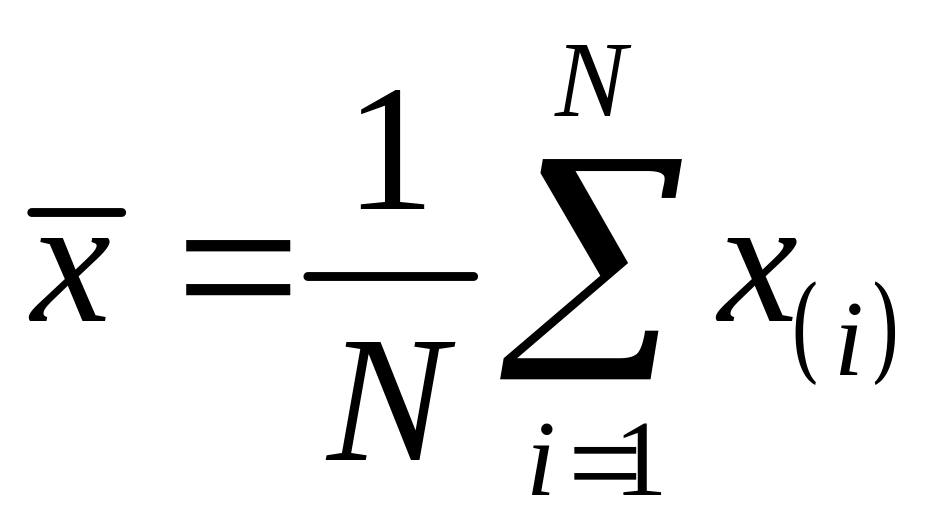В табл.3.5 наведені критичні значення для різних рівнів значимості . Гіпотеза про однорідність отриманих результатів відкидається і максимальне або мінімальне значення виключається з подальшої обробки, якщо або менше критичного значення, заданого в таблиці.

Таблиця 3.5 – Критичні значення для різних рівнів значимості

Кількість дослідів N	Рівень значимості	Рівень значимості	Рівень значимості	Кількість дослідів N	Рівень значимості	Рівень значимості	Рівень значимості
3	0,0109	0,0027	0,0007	14	0,5942	0,5340	0,4792
4	0,0975	0,0494	0,0248	15	0,6134	0,5559	0,5030
5	0,1984	0,1270	0,0808	16	0,6306	0,5755	0,5246
6	0,2826	0,2032	0,1453	17	0,6461	0,5933	0,5442
7	0,3503	0,2696	0,2066	18	0,6601	0,6095	0,5621
8	0,4050	0,3261	0,2616	19	0,6730	0,6243	0,5785
9	0,4502	0,3742	0,3101	20	0,6848	0,6379	0,5937
10	0,4881	0,4154	0,3526	21	0,6958	0,6504	0,6076
11	0,5204	0,4511	0,3901	22	0,7058	0,6621	0,6206
12	0.5483	0,4822	0,4232	23	0,7151	0,6728	0,6327
13	0,5727	0,5097	0,4528	24	0,7238	0,6829	0,6439
				25	0,7319	0,6923	0,6544

Приклад 2.

Було проведено вимірювання відносної прозорості матеріалу і отримано 15 результатів, які після впорядкування подаються таким рядом значень: -0,60; -0,19; -0,13; -0,10; -0,09; -0,06; -0,02; 0,03; 0,04; 0,08; 0,09; 0,17; 0,21; 0,27; 0,43.

Таким чином, маємо мінімальне значення , а максимальне значення і, як можна побачити, вони суттєво відрізняються від значень основної групи. Почнемо з мінімального значення і перевіримо його за критерієм Граббса. Спочатку знайдемо і .

Тоді

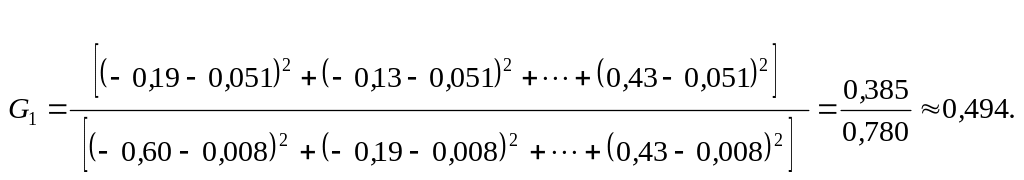
Критичне значення , яке відповідає рівню значимості 0,05, находимо з таблиці 3.5, тобто . Оскільки , то гіпотеза про однорідність сукупності результатів відкидається і мінімальне значення вилучається з результатів.

Якщо для цього мінімального значення застосувати Т-критерій, який був описаний раніше, то для нього отримуємо

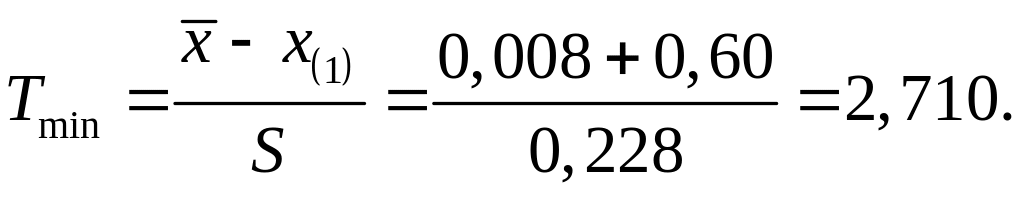
З табл.3.4. визначимо критичне значення .

Таким чином і за цим критерієм необхідно вилучити з ряду значень.

Розглянемо 14 значень, які залишилися в ряду результатів. Перевіримо максимальне значення на наявність грубої помилки. Для ряду з 14 результатами знайдемо і .

Тоді

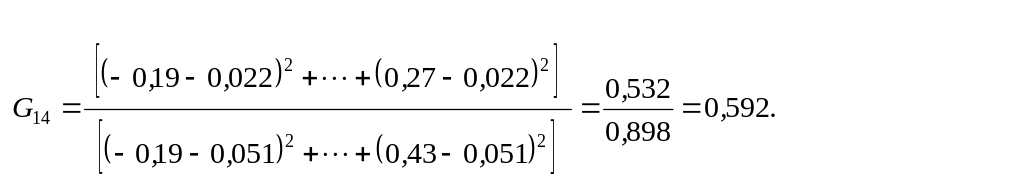
Критичне значення для ряду 14 значень згідно з табл.3.5 буде . Оскільки , то немає підстав вважати грубою помилкою, тобто гіпотеза про однорідність результатів ряду з 14 значень справедлива.

Обмеженням застосування розглянутих методів є те, що результати, які отримані при експериментальному дослідженні, є вибіркою з генеральної сукупності, яка має нормальний закон розподілу. Крім того, вони орієнтовані на виявлення лише однієї грубої помилки. Тому, якщо декілька результатів різняться від основної маси результатів, то необхідно послідовно застосовувати розглянуті методи, як це було зроблено в останньому прикладі. До ряду результатів застосовується один з критеріїв вилучення одного з екстремальних результатів. Коли при перевірці нульової гіпотези з’ясується, що “підозрюваний” результат не є грубою помилкою, то процедура закінчується. В іншому випадку помилковий результат вилучається із ряду результатів і процедура повторюється відносно до значень, які залишилися. Треба відзначити трудність виявлення грубих помилок, яка пов’язана з так званим “маскуючим ефектом”. Результати, які підозрюються в аномальності, часто групуються близько один до одного, створюючи групу, яка дещо відстоїть від основної маси результатів. Це робить послідовні процедури нечутливими до них. В таких випадках треба користуватися узагальненим критерієм Граббса, виходячи з якого американськими статистами Г. Тит’єном і Г. Муром була розроблена процедура виявлення екстремальних результатів [41,42].