
- •Электрические цепи с взаимоиндукцией Напряжение на индуктивно связанных элементах цепи
- •Одноименные зажимы катушек
- •Последовательное соединение индуктивно связанных цепей
- •Экспериментальное определение полярности взаимной индуктивности индуктивно связанных элементов
- •Расчет параллельных цепей с взаимной индукцией
- •Расчет разветвленных цепей с взаимоиндукцией
- •Эквивалентная замена индуктивных связей
- •Трансформаторы Уравнения трансформатора без ферромагнитного сердечника
- •Входное сопротивление трансформатора
- •Входное сопротивление идеального трансформатора
Эквивалентная замена индуктивных связей
В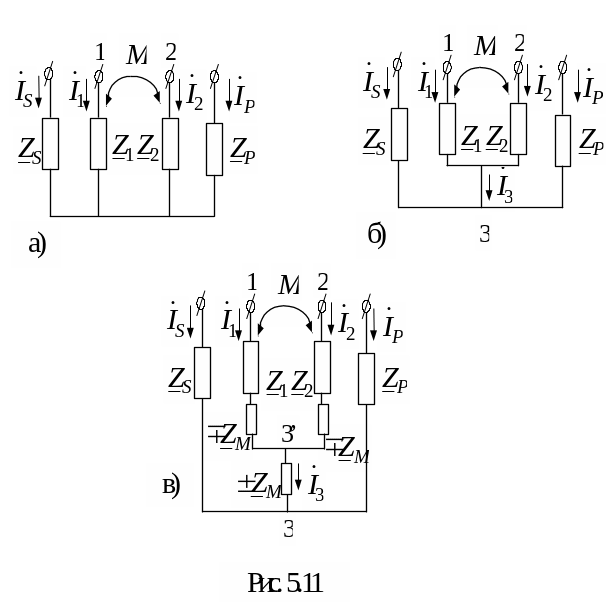 некоторых случаях анализ и расчет
электрических цепей с взаимоиндукцией
можно упростить, если заменить в них
часть схемы с индуктивными связями на
эквивалентную, не содержащую их. Покажем
этот прием, который называется развязкой
индуктивных связей,
на примере схемы рис. 5.11.
некоторых случаях анализ и расчет
электрических цепей с взаимоиндукцией
можно упростить, если заменить в них
часть схемы с индуктивными связями на
эквивалентную, не содержащую их. Покажем
этот прием, который называется развязкой
индуктивных связей,
на примере схемы рис. 5.11.
В схеме на рис. 5.11 имеет место магнитная связь между элементами 1 и 2. Представим электрическую цепь на рис. 5.11, а в виде схемы рис. 5.11, б. Для этой схемы справедливо
![]() (5.18)
(5.18)
Верхний знак
соответствует случаю, когда одноименные
зажимы подключены к одному узлу. Исключим
в (5.18) из первого уравнения
![]() ,
а из второго –
,
а из второго –
![]() :
:
![]() . (5.19)
. (5.19)
При этом
![]() (5.20)
(5.20)
Уравнениям (5.20)
соответствует электрическая цепь на
рис. 5.11, в, в которой магнитные связи
заменены на сопротивления
![]() в ветвях 1
и 2
и
в ветвях 1
и 2
и
![]() в дополнительной третьей ветви,
подключенной в эквивалентной схеме к
месту соединения двух ранее индуктивно
связанных элементов.
в дополнительной третьей ветви,
подключенной в эквивалентной схеме к
месту соединения двух ранее индуктивно
связанных элементов.
Таким образом, при
«развязывании» двух индуктивно связанных
ветвей, подключаемых к одному и тому же
узлу, в эти ветви последовательно
включены сопротивления
![]() ,
а в ветвь между общим узлом и остальной
схемой – сопротивление
,
а в ветвь между общим узлом и остальной
схемой – сопротивление
![]() .
Отсутствие магнитных связей дает
возможность вести расчеты в эквивалентной
схеме всеми методами, основанными на
законе Ома и законах Кирхгофа без
каких-либо ограничений.
.
Отсутствие магнитных связей дает
возможность вести расчеты в эквивалентной
схеме всеми методами, основанными на
законе Ома и законах Кирхгофа без
каких-либо ограничений.
Трансформаторы Уравнения трансформатора без ферромагнитного сердечника
Трансформатор – устройство для передачи энергии из одной цепи в другую посредством электрической индукции. Он предназначен для преобразования величин токов и напряжений, для гальванического разделения электрических цепей, для преобразования сопротивлений по величине и для других целей.
Трансформатор может состоять из двух и более обмоток. Мы будем рассматривать трансформатор из двух разделенных обмоток без ферромагнитного сердечника (воздушный трансформатор), схема которого представлена на рис. 5.12.
Обмотка с зажимами
1-1’, присоединенная к источнику питания,
– первичная,
обмотка, к которой подключается
сопротивление нагрузки
![]() , –
вторичная.
Сопротивление первичной обмотки
, –
вторичная.
Сопротивление первичной обмотки
![]() ,
сопротивление вторичной –
,
сопротивление вторичной –
![]() .
.
У равнения
трансформатора при принятой полярности
катушек и направлении токов имеют вид:
равнения
трансформатора при принятой полярности
катушек и направлении токов имеют вид:
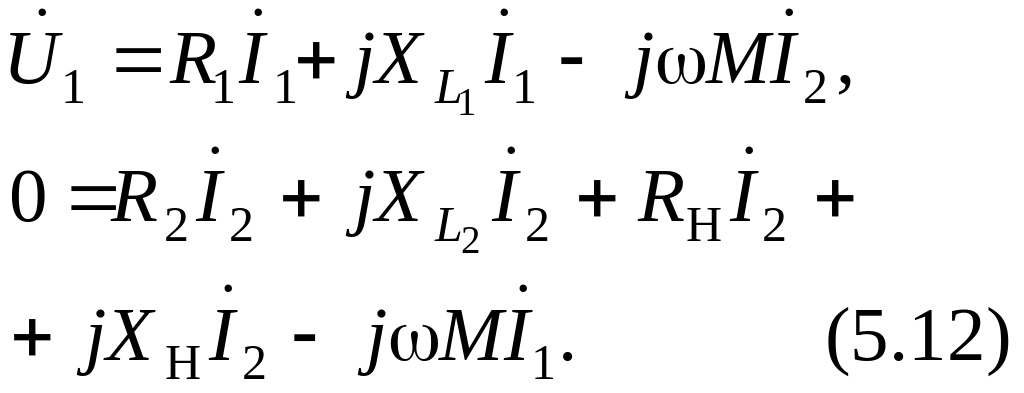 Этим
уравнениям соответствует векторная
диаграмма на рис. 5.13. Построение ее
велось относительно тока
Этим
уравнениям соответствует векторная
диаграмма на рис. 5.13. Построение ее
велось относительно тока
![]() ,
который направлен по действительной
оси.
,
который направлен по действительной
оси.

Входное сопротивление трансформатора
Обозначим
![]() ,
тогда уравнения (5.21) можно переписать
,
тогда уравнения (5.21) можно переписать
 (5.22)
(5.22)
Входное сопротивление
трансформатора
![]() .
Учитывая, что
.
Учитывая, что
![]() и подставляя в первое уравнение (5.21),
получим, что
и подставляя в первое уравнение (5.21),
получим, что
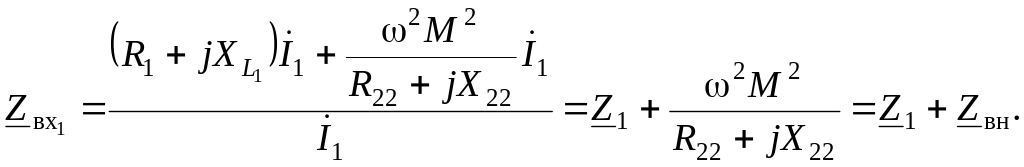 (5.23)
(5.23)
Таким образом,
входное сопротивление трансформатора
со стороны первичных зажимов состоит
из двух слагаемых:
– сопротивление первичной обмотки без
учета взаимоиндукции,
![]() ,
которое появляется за счет явления
взаимоиндукции. Сопротивление
,
которое появляется за счет явления
взаимоиндукции. Сопротивление
![]() как бы добавляется (вносится) из вторичной
катушки и поэтому называется вносимым
сопротивлением.
как бы добавляется (вносится) из вторичной
катушки и поэтому называется вносимым
сопротивлением.
Входное сопротивление идеального трансформатора
Идеальным трансформатором (теоретическое понятие) называют такой трансформатор, в котором выполняются условия
![]() (5.24)
(5.24)
При этом
![]() С определенной погрешностью такие
условия можно выполнить в трансформаторе
с сердечником с высокой магнитной
проницаемостью, на который намотаны
провода с малым активным сопротивлением.
С определенной погрешностью такие
условия можно выполнить в трансформаторе
с сердечником с высокой магнитной
проницаемостью, на который намотаны
провода с малым активным сопротивлением.
Входное сопротивление этого трансформатора
![]() (5.25)
(5.25)
Следовательно,
идеальный трансформатор, включенный
между нагрузкой и источником энергии,
изменяет сопротивление нагрузки
![]() пропорционально квадрату коэффициента
трансформации n.
пропорционально квадрату коэффициента
трансформации n.
С войство
трансформатора преобразовывать
величины сопротивлений широко
используется в различных областях
электротехники, связи, радиотехники,
автоматики и прежде всего с целью
согласования сопротивлений источника
и нагрузки.
войство
трансформатора преобразовывать
величины сопротивлений широко
используется в различных областях
электротехники, связи, радиотехники,
автоматики и прежде всего с целью
согласования сопротивлений источника
и нагрузки.
Схема замещения трансформатора
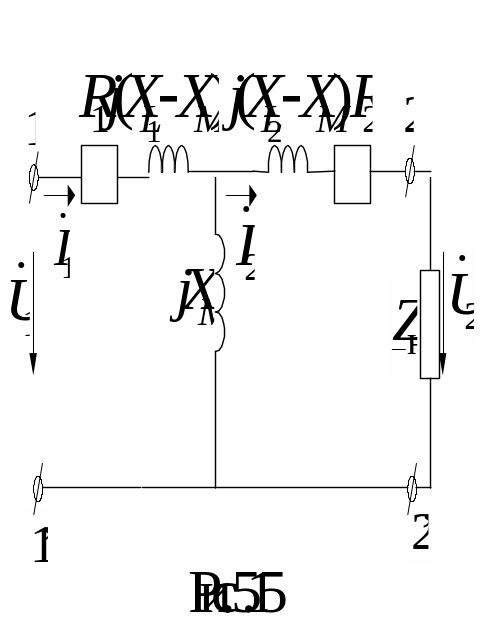
Схема двухобмоточного трансформатора без ферромагнитного сердечника может быть изображена так, как это представлено на рис. 5.14. Токораспределение в ней такое же, что и в схеме на рис. 5.12 без общей точки между обмотками.
Произведем в схеме на рис. 5.14 развязку индуктивных связей. При этом получим схему замещения трансформатора (рис. 5.15), в которой отсутствуют магнитные связи.
Энергетические процессы в индуктивно связанных катушках
Дифференциальные уравнения воздушного трансформатора (рис. 5.15):
 (5.25)
(5.25)
Умножим первое уравнение на , а второе – на :
 (5.26)
(5.26)
Сложив эти уравнения, получим суммарную мгновенную мощность, которая потребляется от источника и расходуется в первичной и в вторичной обмотках трансформатора и в нагрузке
 (5.27)
(5.27)
где ![]() – мгновенная мощность на нагрузке,
– мгновенная мощность на нагрузке,
![]() ;
;
![]() – мгновенная
мощность, расходуемая на тепло в обмотках
трансформатора,
– мгновенная
мощность, расходуемая на тепло в обмотках
трансформатора,
![]() ;
;
![]() – энергия
магнитного поля обмоток трансформатора,
– энергия
магнитного поля обмоток трансформатора,
![]() .
.
