3. Смо с ожиданием

Система массового обслуживания называется системой с ожиданием, если заявка, заставшая все каналы занятыми, становится в очередь. В таких системах важную роль играет так называемая «дисциплина очереди». Ожидающие в очереди заявки могут поступать на обслуживание как в порядке очереди, так и в случайном порядке. Существют системы массового обслуживания с приоритетом, когда некоторые выделяемые по какому-либо признаку заявки обслуживаются в первую очередь.

Каждый тип системы с ожиданием имеет свои особенности и свою математическую теорию. Рассмотрим один из самых простых вариантов смешанной системы обслуживания, часто встречающийся на практике.

Пусть на вход n-канальной системы обслуживания поступает простейший поток требований с плотностью . Время обслуживания каждой из заявок распределено по показательному закону с параметром . Заявка, заставшая все каналы системы занятыми, становится в очередь и ожидает обслуживания. Время ожидания будем считать случайным и распределенным по показательному закону

где .

Введем допущение о том, что входящий поток является простейшим, а с учетом того, что распределение времени обслуживание и времени ожидания – показательные, то процесс функционирования системы можно считать Марковским. Перечислим состояния системы.

свободны все каналы системы, очереди нет;

занят ровно один канал, очереди нет;

^{………………………………………………………………………}

занято ровно k каналов, очереди нет;

^{………………………………………………………………………}

заняты все n каналов, очереди нет;

заняты все n каналов, одна заявка стоит в очереди;

^{……………………………………………………………………}

заняты все n каналов, s заявок стоят в очереди.

Поскольку число заявок s, ожидающих обслуживание в очереди, может быть сколь угодно большим, система имеет бесконечное число состояний.

Анализ системы с ожиданием проведем аналогично тому, как это было сделано для системы с отказами.

(рис.)

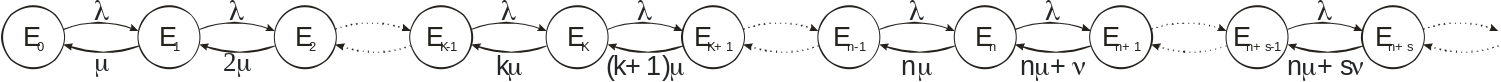
Соответствующая система алгебраических уравнений имеет вид:

К полученной системе уравнений необходимо добавить еще одно

.

Применим для решения этой системы алгебраических уравнений уже использованный ранее прием. Введем

При этом система уравнений перепишется в виде

Отсюда Следовательно

.

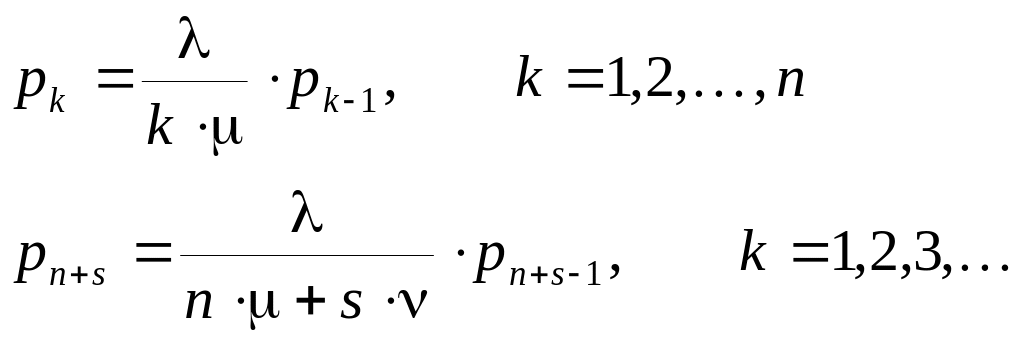Тогда

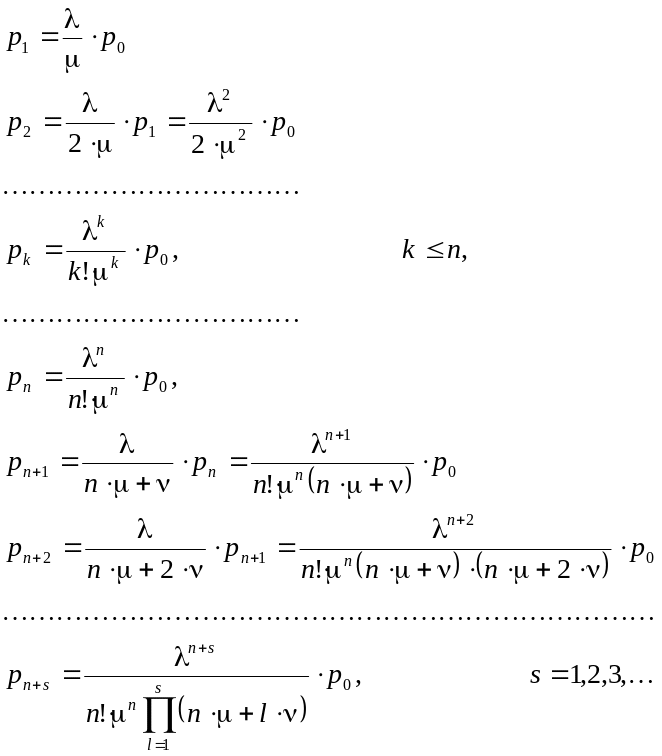
Заметим, что первые n формул совпадают с формулами для системы с отказами.

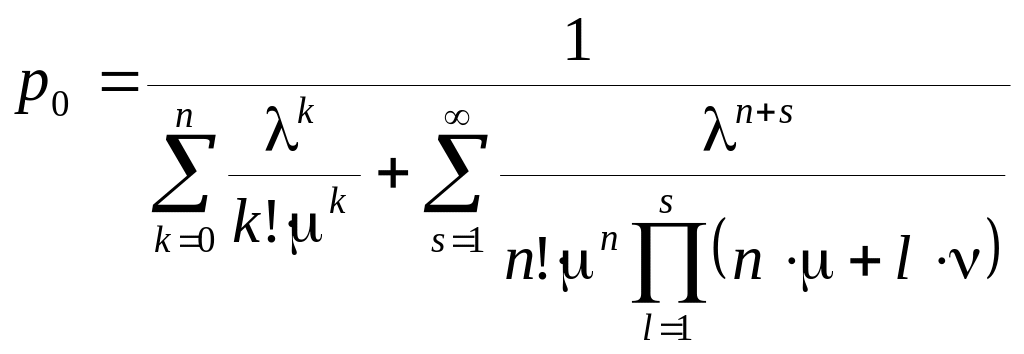
Введем .

Параметры и выражают соответственно среднее число заявок и среднее число уходов заявок, стоящих в очереди, приходящиеся на среднее время обслуживания одной заявки.

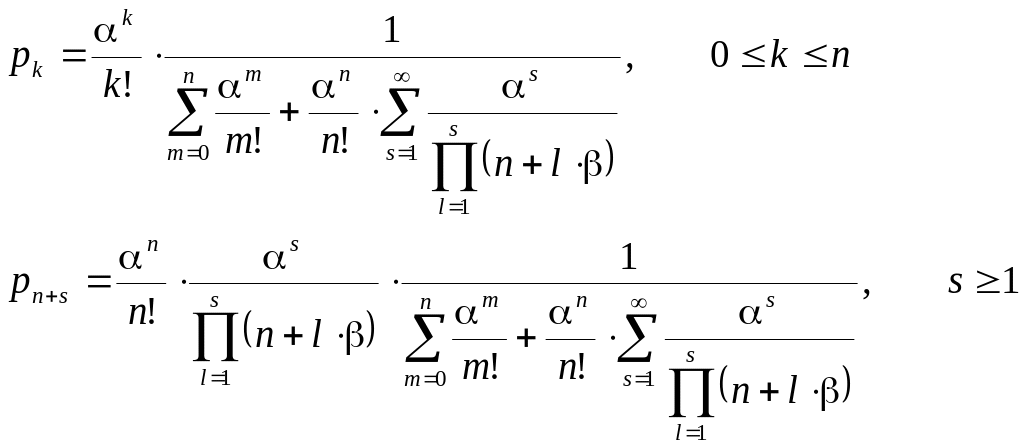
Непосредственное использование этих формул затруднено тем, что в них входят бесконечные суммы. Однако члены этих сумм быстро убывают (если ). Заметим, что когда параметр ( ), рассматриваемая система превращается в систему с отказами (заявка мгновенно уходит из очереди).

Полученные формулы позволяют получить количественные оценки системы обслуживания и для другого крайнего случая, когда время ожидания в очереди неограниченно велико (чистая система с ожиданиями). В такой системе заявки вообще не покидают очереди.

В чистой системе с ожиданием не всегда имеется стационарный режим. Такой режим существует лишь в случаях, если , т.е. среднее число поступающих заявок, приходящееся на среднее время обслуживания одной заявки, не превышает возможностей n-канальной системы. В противном случае ( ) число заявок, ожидающих обслуживания в очереди, будет неограниченно возрастать.

Найдем предельные вероятности состояний чистой системы с ожиданием для . Для этого положим параметр .

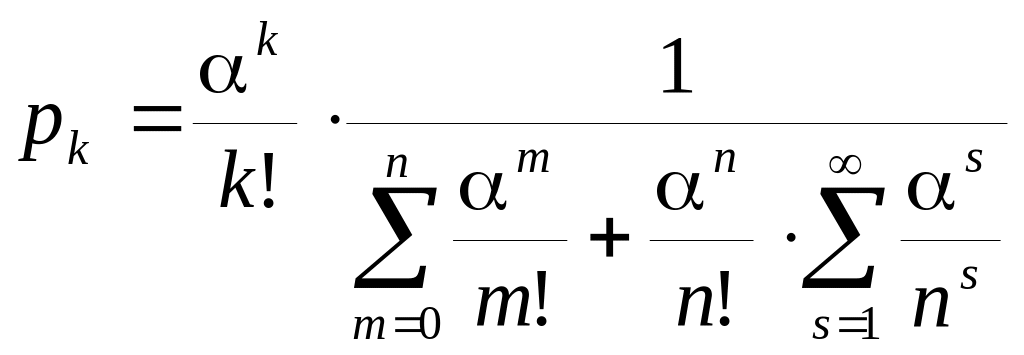
Суммируя бесконечно убывающую геометрическую прогрессию получим

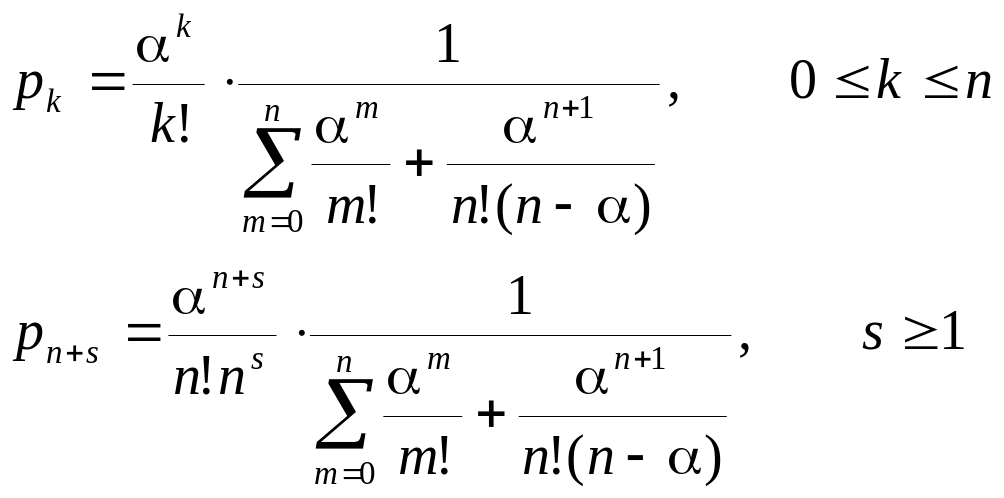
Вычислим среднее число заявок, находящихся в очереди:

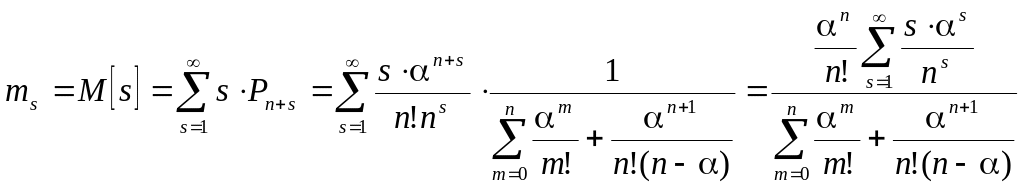
С целью упрощения этого выражения просуммируем арифметико-геометрическую прогрессию . Введя , имеем

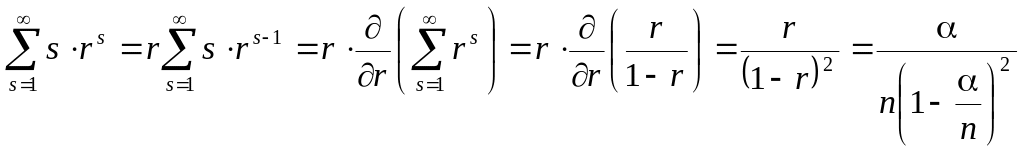
Тогда

.

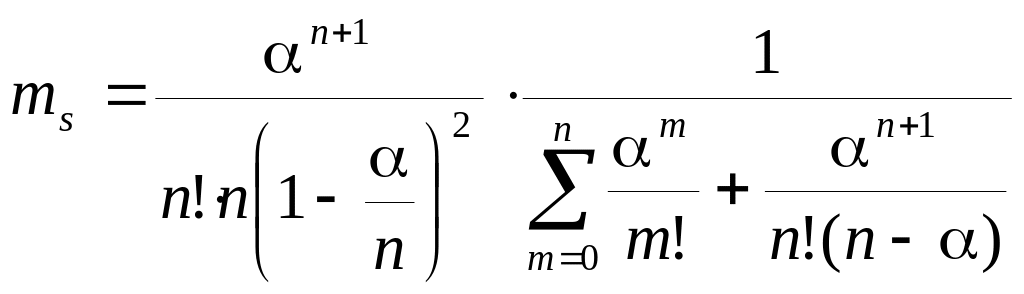Получим теперь формулу для расчета среднего времени ожидания заявки в очереди.

Если в момент поступления заявки хотя бы один из каналов системы свободен, то время ожидания, естественно равно нулю. Если заявка поступает в момент, когда все каналы системы заняты, но очереди нет, то время ожидания в среднем равно (так как поток освобождения в n-канальной системе имеет плотность ). Если заявка застанет все каналы занятыми и одну заявку в очереди, то среднее время ожидания равно и т.д. Поэтому среднее время ожидания начала обслуживания равно

Поскольку

то

.

Таким образом, среднее время ожидания начала обслуживания равно среднему числу заявок, ожидающих в очереди, деленному на плотность потока заявок.