Лабораторная работа №5. Оптимизационные задачи в экономике

Цель работы:

• изучить технологию решения задач линейного программирования в MS EXCEL;

• получить практические навыки использования функции Поиск решения для решения экономических задач.

Результат обучения. После обучения студент должен:

• уметь строить математические модели для реальных экономических задач;

• знать основные возможно­сти табличного процессора EXCEL и использовать их для решения эко­номических задач;

• уметь решать экономические задачи с помощью функции Поиск решения.

Продолжительность занятия – 4 часа.

1.1.Общие положения

Для понимания сути оптимизационных задач рассмотрим практический пример. Предположим, что магазин торгует магнитолами по цене 1500 руб. и телевизорами по цене 3000 руб. Требуется определить, сколько нужно продавать в день магнитол и телевизоров, чтобы выручка была максимальной.

Очевидный ответ будет таким: как можно больше телевизоров и как можно больше магнитофонов. При этом математическое уравнение будет иметь следующий вид:

S=1500*m+3000*n,

где S – выручка магазина,

m – количество проданных магнитол;

n – количество проданных телевизоров.

Реальные возможности магазина ограничены. Например, в день можно продать не более 70 магнитол и не более 50 телевизоров. Очевидно, что m и n не могут быть отрицательными значениями. Поэтому задав ограничения:

m<=50

n<=70

n>=0

m>=0

мы получим математическую модель, которую можно использовать для моделирования экономической ситуации.

Рассмотренный пример относится к области линейного программи­рования. Большое количество экономических задач сводятся к линейному программированию. Задачи линейного программирования можно решать, используя MS EXCEL.

1.2.Планирование производства

Завод выпускает два вида стали: легированную сталь и нелегированную сталь. Для производства стали используется руда от двух поставщиков: уральская руда и сибирская руда. Максимально возможные суточные запасы этих продуктов на складе завода составляют 20 т и 40 т соответственно. Расходы руды на производство 1 т. стали приведены в таблице 1.

Таблица 1 Расходы руды на производство стали

Исходный продукт	Расход на 1 т. стали		Максимальный запас руды
	Легированная сталь	Нелегиро­ван­ная сталь
Уральская руда Сибирская руда	2 3	3 4	20 40

Анализ рынка показал, что суточный спрос на нелегированную сталь меньше спроса на легированную сталь не более чем на 2 т. Кроме того, установлено, что спрос на легированную сталь не превышает 10 т. в сутки. Прибыль от продажи одной тонны стали равны 4 000 р. и 3 000 р. соответственно. Необходимо найти общее количество выпускаемой стали, при котором при­быль максимальна.

Для решения задачи построим сначала математическую модель. Суммарная суточная прибыль от продажи стали составляет:

P=4000*L1+3000*L2,

где L1 – количество легированной стали

L2 – количество нелегированной стали

Перейдем к ограничениям. Объем производства не может быть отрицательным, следовательно

L1, L2 =>0

Расход исходного сырья не может превосходить максимального запаса, следовательно

2* L1 + 3* L2 <=20,

3* L1 + 4* L2 <=40.

Ограничение на спрос таковы, что должны выполняться неравенства

L1 – L2 <=2,

L1 <=10.

Теперь решим задачу, для чего выполните следующие действия.

1. Создайте таблицу по образцу, приведенному ни ниже (Рис. 45).

Рис. 1. Исходная таблица

2. Введите теперь формулы математической модели (Рис. 46).

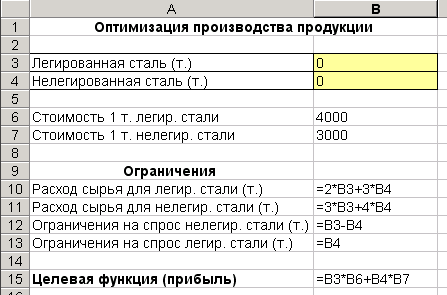
Рис. 2. Формулы математической модели

3. Выполните команду Сервис – Поиск решения.

4. В открывшемся окне задайте следующие параметры:

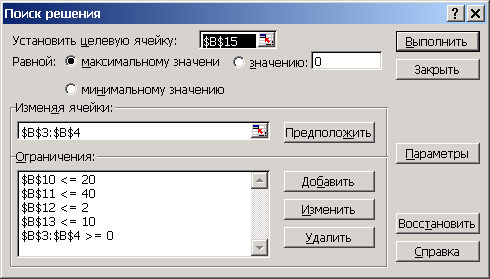
Рис. 3. Параметры поиска решения

5. После команды Выполнить откроется окно диалога Результаты поиска решения, которое сообщает, что решение найдено.

6. Создайте отчет о решении. Для этого выберите тип отчета - Результаты. Нажмите ОК.

7. В результате будут рассчитаны оптимальные значения производства стали (Рис. 48).

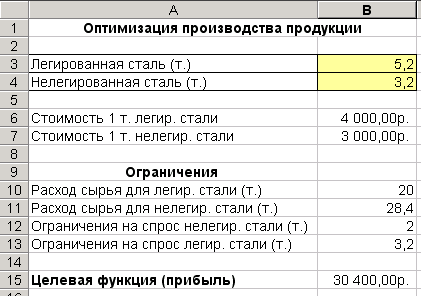
Рис. 4. Результаты решения

8. Для просмотра полученного отчета в рабочей книге (Рис. 49) выберите появившийся корешок.

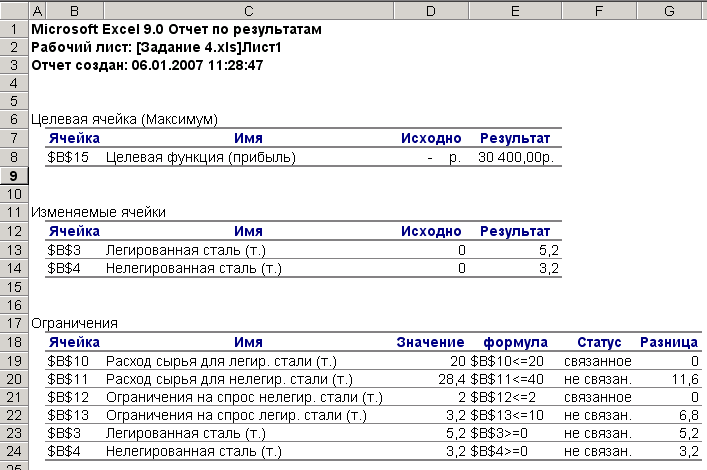
Рис. 5. Отчет по результатам решения