1.2.2. Статические и динамические свойства объектов регулирования

Производственные процессы в объектах регулирования всегда представляют собой процессы преобразования, обмена материалов или энергии.

Пример процесса материального обмена был приведен на рис. 1.6, где показана система регулирования давления в рабочем пространстве печи. Примером энергетического обмена может служить процесс подогрева воздуха газообразными продуктами сгорания в подогревателе (рис. 1.10). Тепловая энергия продуктов сгорания, энергия подачи, передается здесь воздуху, т.е. переходит в энергию потребления. Количество поступающей тепловой энергии зависит от количества и температуры продуктов сгорания. Часть этой энергии аккумулируется в стенках и всей массе конструкции подогревателя, часть ее теряется с выходящими из подогревателями продуктами сгорания и в окружающую среду. Остальная энергия используется для нагрева воздуха. Температура подогрева воздуха зависит при этом от энергии подачи и от количества воздуха и его начальной температуры. В данном случае температура подогрева воздуха – это выходная, регулируемая величина рассматриваемого объекта регулирования. В условиях равновесия, когда имеет место равенство энергии подачи и энергии потребления, т.е. установившееся состояние, выходная величина не меняет своего значения; она будет изменяться при

21

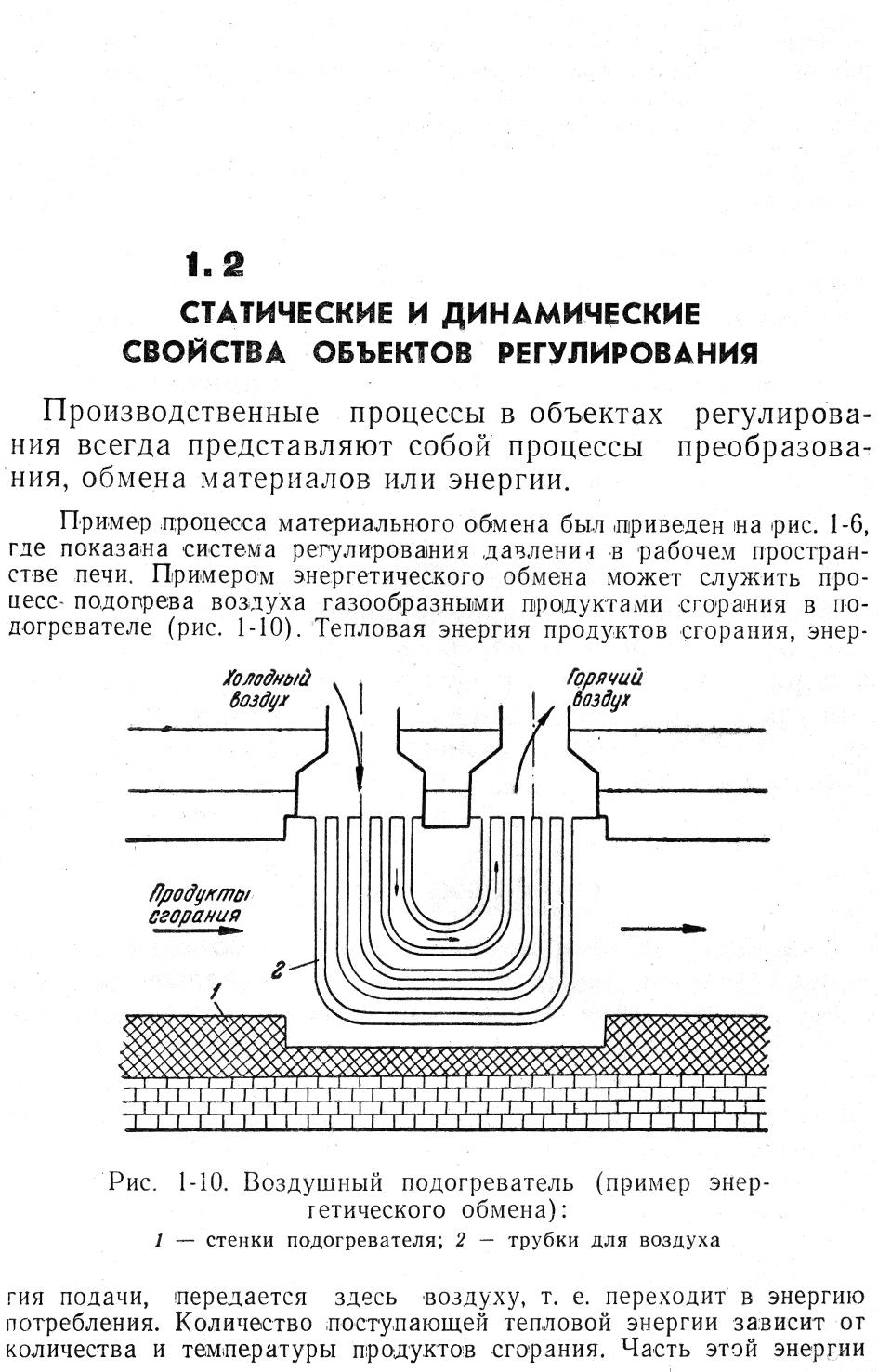
Рис. 1.10. Воздушный подогреватель (пример энергетического

обмена): 1 – стенки подогревателя; 2 – трубки для

воздуха

нарушениях этого равновесия.

Физическая природа регулируемых величин может быть различной в разных объектах. Это могут быть давление, температура, уровень или положение, скорость и т.п. Для решения задач регулирования необходимо знать общие свойства объекта – его динамические и статические характеристики вне зависимости от физической природы и конструктивных особенностей агрегата и происходящего в нем процесса, ибо именно эти характеристики определяют условия регулирования. Статические и динамические характеристики объекта необходимы для расчета системы автоматического регулирования: выбора принципиальной схемы регулирования, регуляторов и их настроек, средств измерения регулируемых величин и регулирующих органов, т.е. для синтеза системы автоматического регулирования. Они необходимы также для анализа устойчивости и качества работы системы регулирования.

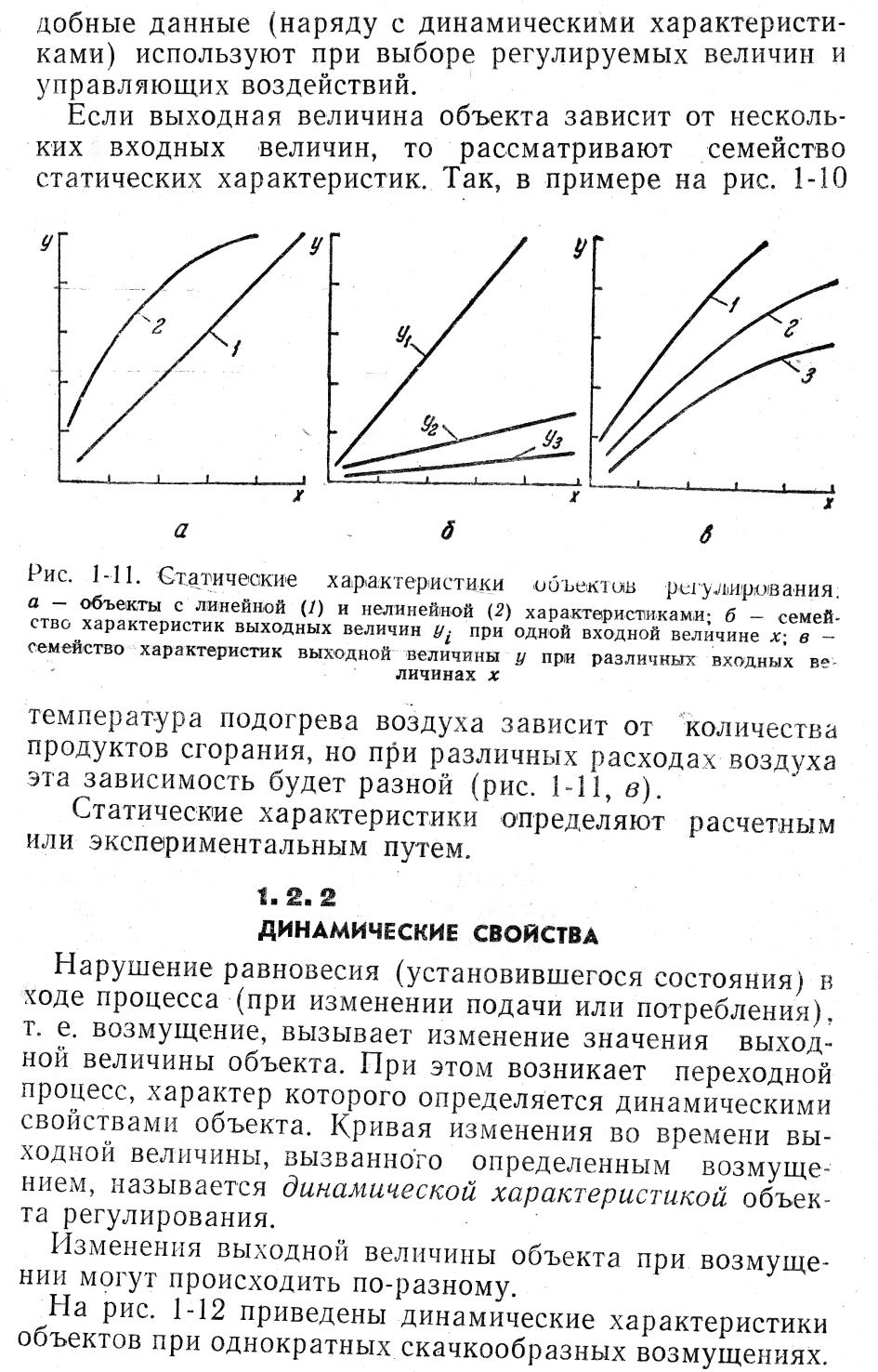
Статические свойства

Каждому значению входной величины объекта в установившемся состоянии соответствует определенное значение его входной величины. Зависимость между выходной и входной величинами в установившихся состояниях называется статической

22

характеристикой объекта регулирования. Эта зависимость может быть как линейной, так и нелинейной (рис. 1.11, а).

Статические характеристики объекта позволяют оценивать степень связи между различными выходными и входными величинами объекта; в примере на рис. 1.11, б выходная величина зависит от входной величины значительно больше, чем другие выходные величины. Подобные данные (наряду с динамическими характеристиками) используют при выборе регулируемых величин и управляющих воздействий.

Если выходная величина объекта зависит от нескольких входных величин, то рассматривают семейство статических характеристик. Так, в примере на рис. 1.10 температура подогрева

а б в

Рис. 1.11. Статические характеристики объектов регулирования:

а – объекты с линейной (1) и нелинейной (2) характе –

ристиками; б – семейство характеристик выходных ве-

личин при одной входной величине ; в – семейст-

во характеристик выходной величины при различн-

ых входных величинах

воздуха зависит от количества продуктов сгорания, но при различных расходах воздуха эта зависимость будет разной (рис. 1.11, в).

Статические характеристики определяют расчетным или экспериментальным путем.

Динамические свойства

Нарушение равновесия (установившегося состояния) в ходе процесса (при изменении подачи или потребления), т.е. возмущение, вызывает изменение значения выходной величины

23

Объекта. При этом возникает переходной процесс, характер которого определяется динамическими свойствами объекта. Кривая изменения во времени выходной величины, вызванного определенным возмущением, называется динамической характеристикой объекта регулирования.

Изменения выходной величины объекта при возмущении могут происходить по-разному.

На рис. 1.12 приведены динамические характеристики объектов при однократных скачкообразных возмущениях.

Подавляющее большинство объектов обладает способностью постепенно приостанавливать отклонение выходной величины от первоначального значения, т.е. в них вновь устанавливается равновесие. Однако это будет уже новое установившееся состояние: равновесие наступит при изменившихся расходах энергии и др., а также при новом значении выходной величины объекта.

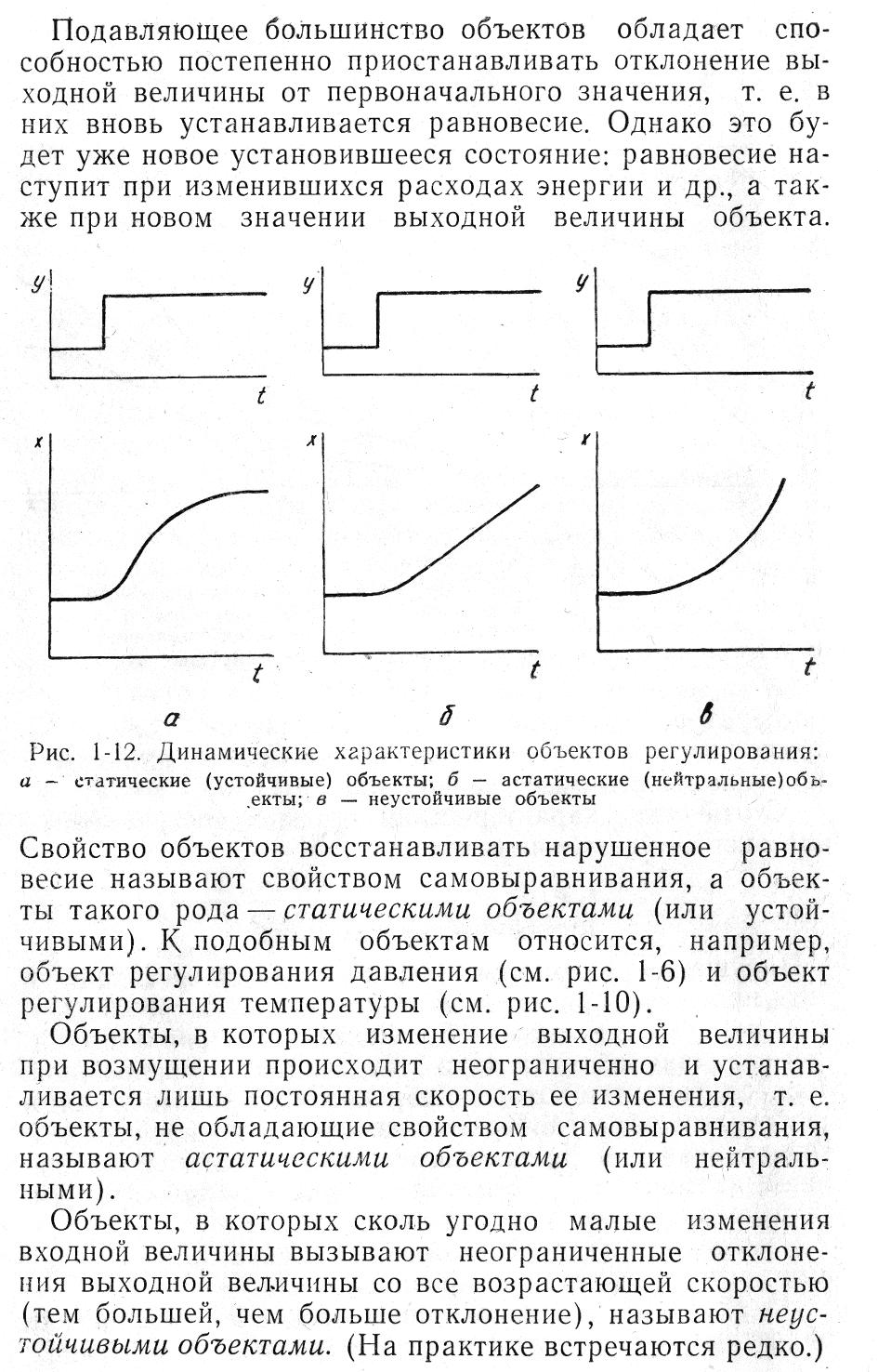
а б в

Рис. 1.12. Динамические характеристики объектов регулирования:

а – статические (устойчивые) объекты; б – астатические

(нейтральные) объекты; в – неустойчивые объекты

Свойство объектов восстанавливать нарушенное равновесие называют свойством самовыравнивания, а объекты такого рода – статическими объектами (или устойчивыми). К подобным объектам относится, например, объект регулирования давления (см. рис. 1.6) и объект регулирования температуры (см. рис. 1.10).

Объекты, в которых изменение выходной величины при возмущении происходит неограниченно и устанавливается лишь постоянная скорость ее изменения, т.е. объекты, не обладающие

24

свойством самовыравнивания, называют астатическими объектами (или нейтральными).

Объекты, в которых сколь угодно малые изменения входной величины вызывают неограниченные отклонения выходной величины со все возрастающей скоростью (тем большей, чем больше отклонение), называют неустойчивыми объектами. (на практике встречаются редко.)

Для того чтобы регулирование было эффективным, необходимо пи возникновении возмущения как можно быстрее и точнее ввести регулирующее воздействие. В замкнутой системе регулятор получает сигнал о возмущении лишь после того, как регулируемая величина отклонилась от задания. Чем быстрее может быть замечено отклонение, тем лучше условия для регулирования.

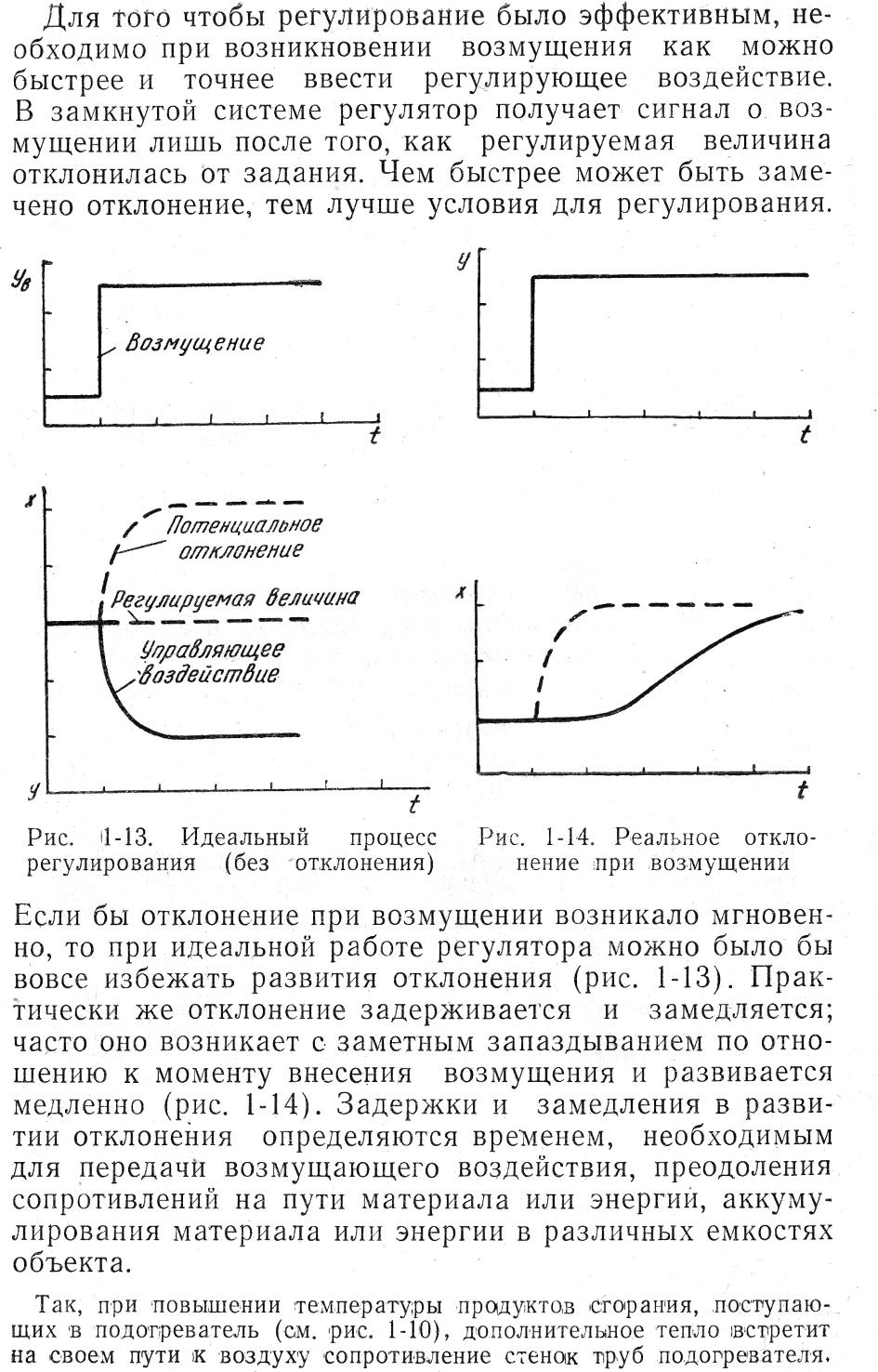
Рис. 1.13. Идеальный процесс регули- Рис. 1.14. Реальное отклонение

рования (без отклонения) при возмущении

Если бы отклонение при возмущении возникало мгновенно, то при идеальной работе регулятора можно было бы вовсе избежать развития отклонения (рис. 1.13). Практически же отклонение задерживается и замедляется; часто оно возникает с заметным запозданием по отношению к моменту внесения возмущения и развивается медленно (рис. 1.14). Задержки и

25

замедления в развитии отклонения определяются временем, необходимым для передачи возмущающего воздействия, преодоления сопротивлений на пути материала или энергии в различных емкостях объекта.

Так, при повышении температуры продуктов сгорания, поступающих в подогреватель (см. рис. 1.10), дополнительное тепло встретит на своем пути к воздуху сопротивление стенок труб подогревателя и будет аккумулироваться в этих трубах и стенках подогревателя, а также в нагреваемом воздухе. Это задерживает повышение температуры воздуха, достижение нового значения температуры. Кроме того, повышение температуры будет отмечено регулятором с запаздыванием, величина которого определяется расстоянием до места измерения температуры и скоростью потока нагреваемого воздуха. При регулировании давления в рабочем пространстве печи (см. рис. 1.6) потоки газов и воздуха преодолевают сопротивление в трубопроводах, клапанах, насадках и др., аккумулируются в этих емкостях и в емкости рабочего пространства.

Объекты регулирования всегда представляют собой последовательные соединения различных физических емкостей и сопротивлений (тепловых, гидравлических, электрических и др.). На рис. 1.15 показана структура подогревателя в виде схемы соединений емкостей и сопротивлений.

Рис. 1.15. Структура воздушного подогревателя (см. рис. 1.10):

- тепловая емкость кладки; - сопротивление

трубок теплопередаче; - тепловая емкость воз-

духа

Число пар сопротивления – емкость на пути материала или энергии определяет характер динамических характеристик объекта; в зависимости от их числа принято различать одноемкостные и многоемкостные объекты. Чем больше величины сопротивления и емкости, тем медленнее нарастает отклонение, тем больше время

26

установления нового значения регулируемой величины (рис. 1.16, а). Чем больше число пар сопротивление – емкость, тем более S-образный характер носят кривые реакции выходной величины объекта на возмущение (рис. 1.16, б). Запаздывание передачи (транспортное запаздывание), не изменяя характера кривой изменения регулируемой величины, приводит к смещению ее по оси времени от момента внесения возмущения (рис. 1.16, в). Изменение одной и той же регулируемой величины объекта может иметь различный характер по отношению к различным возмущениям, например к изменению подачи либо потребления. Так, по отношению к изменению расхода воздуха через подогреватель (см. рис. 1.10) объект регулирования температуры

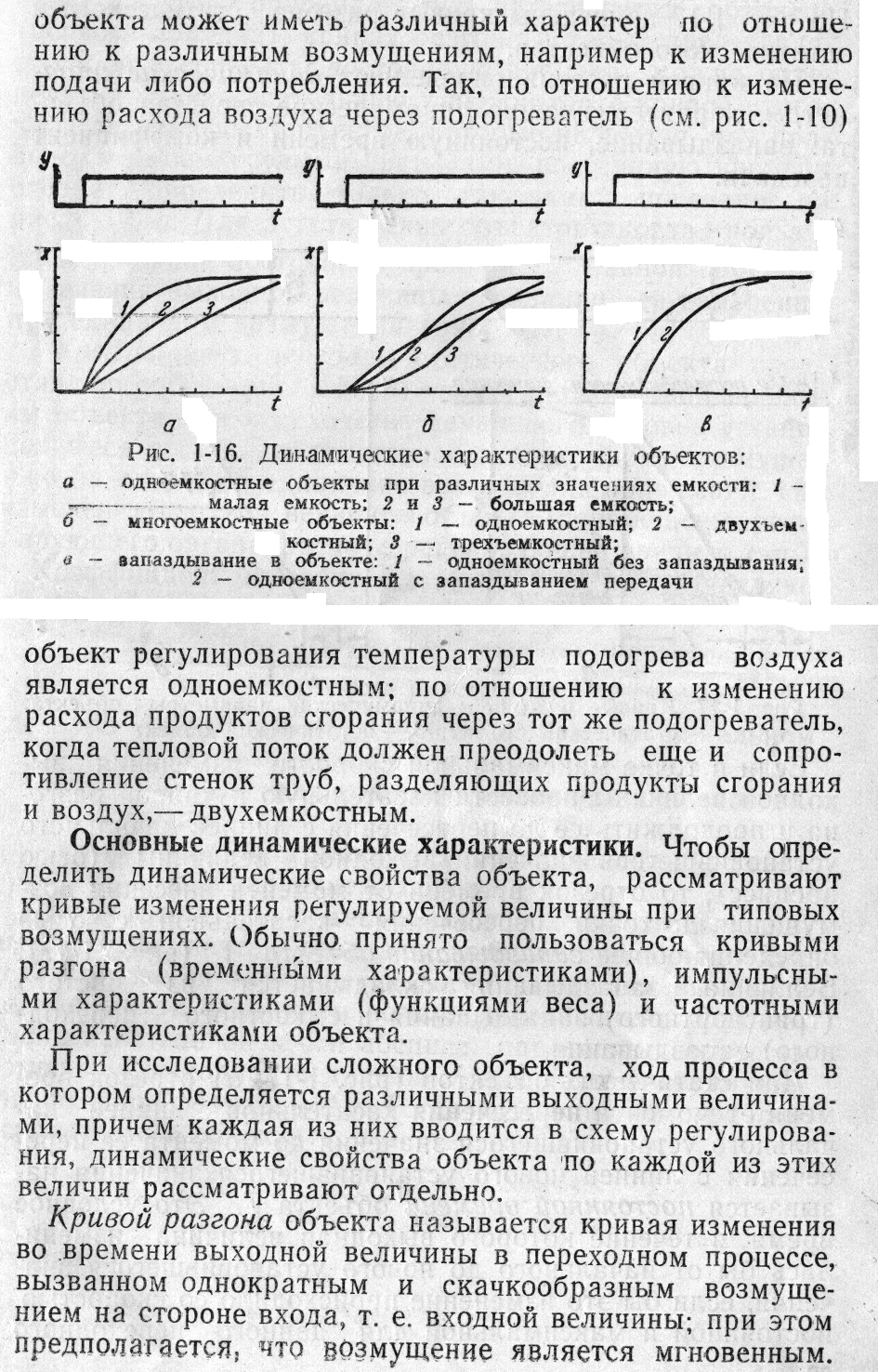
Рис. 1.16. Динамические характеристики объектов: а – одноемкост-

ные объекты при различных значениях емкости: 1 – малая

емкость; 2 и 3 – большая емкость; б – многоемкостные

объекты : 1 – одноемкостный; 2 – двухъемкостный; 3 –

трехъемкостный ; в – запаздывание в объекте: 1 – одноем-

костный без запаздывания; 2 – одноемкостный с запазды-

ванием передачи

подогрева воздуха является одноемкостным: по отношению к изменению расхода продуктов сгорания через тот же подогреватель, когда тепловой поток должен преодолеть еще и сопротивление стенок труб, разделяющих продукты сгорания и воздух, - двухемкостным.

Основные динамические характеристики. Чтобы определить динамические свойства объекта, рассматривают кривые изменения регулируемой величины при типовых возмущениях. Обычно принято пользоваться кривыми разгона (временными характеристиками), импульсными характеристиками (функциями веса) и частотными характеристиками объекта.

При исследовании сложного объекта, ход процесса в котором определяется различными выходными величинами, причем каждая

27

из них вводится в схему регулирования, динамические свойства объекта по каждой из этих величин рассматривают отдельно.

Кривой разгона объекта называется кривая изменения во времени выходной величины в переходном процессе, вызванном однократным и скачкообразным возмущением на стороне входа, т.е. входной величины; при этом предполагается, что возмущение является мгновенным. На рис. 1.17 приведены кривые разгона статического и астатического объектов.

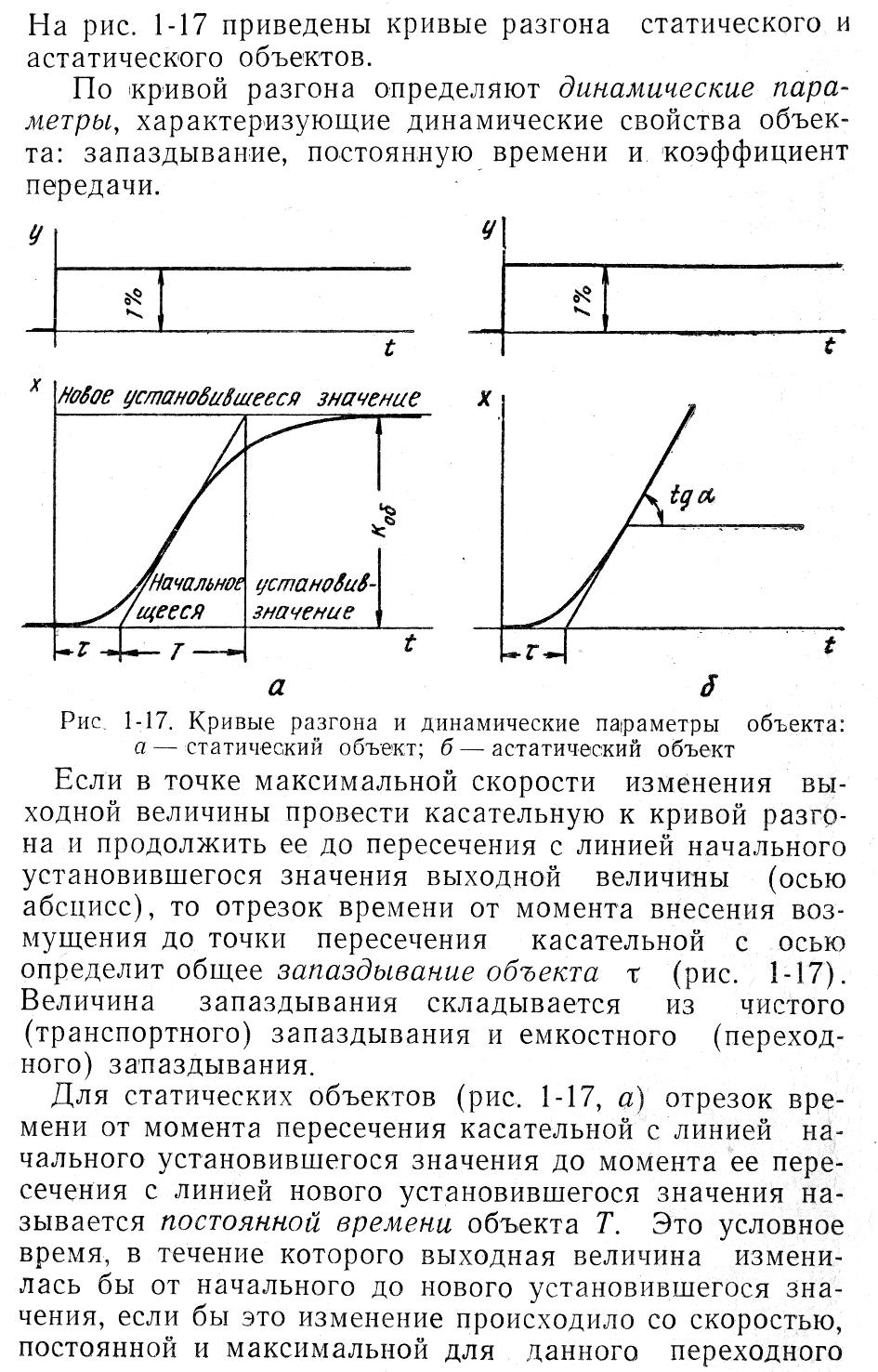
Рис. 1.17. Кривые разгона и динамические параметры объекта:

а – статический объект; б – астатический объект

По кривой разгона определяют динамические параметры, характеризующие динамические свойства объекта: запаздывание, постоянную времени и коэффициент передачи.

Если в точке максимальной скорости изменения выходной величины провести касательную к кривой разгона и продолжить ее до пересечения с линией начального установившегося значения выходной величины (осью абсцисс), то отрезок времени от момента внесения возмущения до точки пересечения касательной с осью определить общее запаздывание объекта τ (рис. 1.17). Величина запаздывания складывается из чистого (транспортного) запаздывания и емкостного (переходного) запаздывания.

Для статических объектов (рис. 1.17, а) отрезок времени от момента пересечения касательной с линией начального установившегося значения до момента ее пересечения с линией нового установившегося значения называется постоянной времени объекта Т. Это условное время, в течении которого выходная

28

величина изменилась бы от начального до нового установившегося значения, если бы это изменение происходило со скоростью, постоянной и максимальной для данного переходного процесса. Для одноемкостных статических объектов (первого порядка), кривая разгона которых представляет собой экспоненту, постоянную времени можно определить как подкасательную к любой точке кривой разгона. Для реальных объектов, которые являются, как правило, многоемкостными системами, постоянную времени следует определять только так, как показано на рис. 1.17, а. Для астатических объектов иногда пользуются условной постоянной времени , равной времени изменения входной величины на единицу е измерения при единичном возмущении (рис. 1.17, б).

Коэффициент передачи статического объекта представляет собой (рис. 1.17, а) изменение выходной величины объекта при переходе из начального в новое установившееся состояние, отнесенное к единичному возмущению на входе. За единичное возмущение принимают 1% изменения входной величины объекта (перемещения регулирующего органа, расхода регулирующей среды и т.п.).

Коэффициент передачи (рис. 1.17, а) вычисляют по кривой разгона:

,

где - значение выходной величины в начальном установивше

мся состоянии;

- то же для нового установившегося состояния;

- величина вносимого возмущения, % хода регулирующего

органа.

Для астатических объектов иногда пользуются условным коэффициентом передачи, который определяют как установившееся значение скорости изменения выходной величины при единичном возмущении. Тангенс угла наклона касательной к оси абсцисс определяет скорость изменения выходной величины при данном возмущении входной величины . Тогда коэффициент передачи астатического объекта

.

29

Очевидно:

.

Возможность оценки динамических свойств объекта параметрами , и обусловлена тем, что с достаточной для практических задач степенью точности можно аппроксимировать сложные, многоемкостные объекты структурно более просто – как последовательное включение двух элементарных звеньев: звена с чистым запозданием и апериодического звена с постоянной времени и коэффициентом передачи .

Характерным показателем динамических свойств объекта и условий регулирования является величина отношения запаздывания к постоянной времени . В общем случае чем меньше отношение / , тем благоприятнее условия для регулирования; чем / больше, тем условия для регулирования труднее.

Импульсной характеристикой объекта называется кривая изменения во времени выходной величины в переходном процессе, вызванном однократным импульсивным возмущением входной

а б

Рис. 1.18. Импульсные характеристики объекта:

а – статический объект; б – астатичес-

кий объект

величины, т.е. возмущением бесконечно большой величины и бесконечно

30

малой продолжительности (рис. 1.18).

По импульсной характеристике объекта можно рассчитать реакцию объекта (изменение выходной величины) при произвольном изменении его входной величины.

По импульсной характеристике, как и по кривой разгона, можно определить динамические параметры объекта: , и .

Частотная (амплитудно-фазовая) характеристика представляет собой реакцию объекта (изменение регулируемой величины) при периодических изменениях входной величины (рис. 1.19, а).

Если на вход объекта подается возмущающее воздействие вида

,

где - амплитуда колебаний;

- их частота,

то по истечении некоторого промежутка времени на выходе возникнут установившиеся колебания выходной величины с той же частотой , но амплитудой В и некоторым сдвигом фаз относительно входных колебаний, т.е. вида

.

Амплитуда выходных колебаний В и сдвиг фаз этих колебаний φ определяют физическими свойствами объекта и зависят лишь от частоты колебаний ω.

Кривая зависимости отношения амплитуд от частоты М(ω)=В/А является амплитудно-частотной характеристикой объекта, а кривая φ(ω) – его фазо-частотной характеристикой. (рис.1.19, б)

Зависимость между выходными и входными колебаниями рассматриваемого объекта для каждой данной частоты можно графически представить на комплексной плоскости вектором. Совокупность векторов представляет амплитудно-фазовую характеристику, которую можно представить в виде годографа, кривой, соединяющей концы этих векторов, на которой отмечены соответствующие частоты колебаний (рис. 1.19, в).

Проекции вектора на оси координат в функции частоты колебаний Re(ω) и Im(ω) называются действительными и мнимыми частотными характеристиками объекта.

Кривые разгона, импульсные характеристики и частотные характеристики взаимосвязаны и выражают одни и те же свойства объекта (они являются решением одних и тех же

31

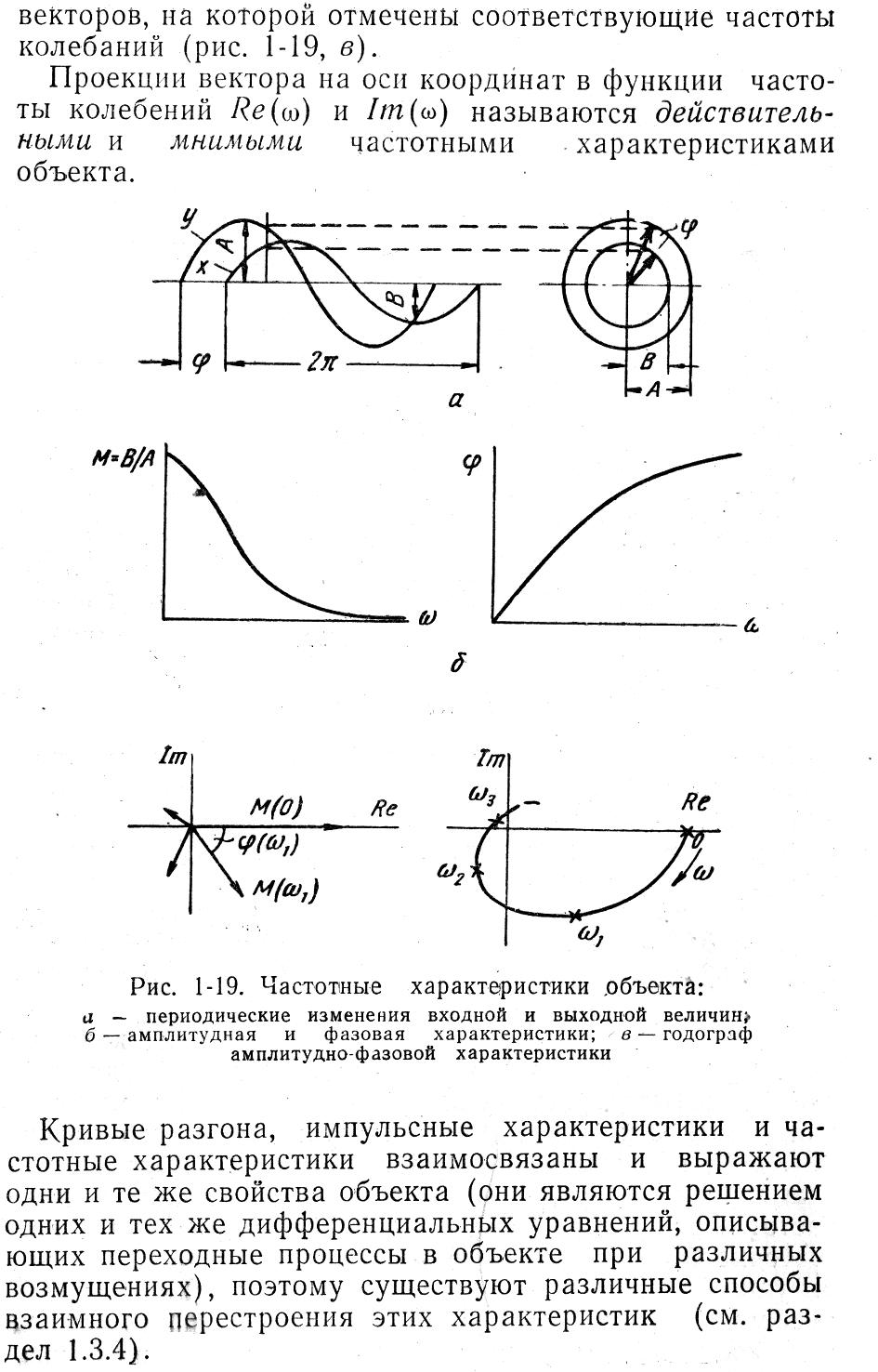
в

Рис. 1.19. Частотные характеристики объекта: а – периодические

изменения входной и выходной величин; б – амплитуд

ная и фазовая характеристики; в – годограф амплитуд-

но-фазовой характеристики

дифференциальных уравнений, описывающих переходные процессы в объекте при различных возмущениях), поэтому существуют различные способы взаимного перестроения этих характеристик.