14)Закон больших чисел. Центральная предельная теорема.
Закон больших чисел:Если
независимые
однотипные CВ с математическим
ожиданием а, тогда
.
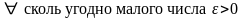
Центральная предельная теорема– это группа теорем об условиях, при которых возникает нормальный закон распределения.
При
изучении нормального закона была
сформулирована теорема: если
– независимые нормальные случайные
величины с
одними и теми же параметрам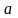и
и
,
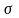то их сумма
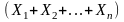также
нормальна и имеет параметры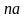
и
.
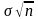Кроме того,
справедливо равенстводля
любого сколь угодно малого
числа
.
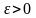Это равенство практически точно уже
при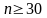
.
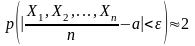Ф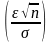
Это утверждение называется центральной предельной теоремой и кратко формулируется так: сумма большого числа независимых однотипных случайных величин с любым законом распределения приближенно нормальна.
теорема Ляпунова: если случайные величины независимы и никакая из них не доминирует над другими, то при достаточно большом числе слагаемых их сумма приближенно нормальна.
-незав. СВ
MX=a,
DX=σ2
;
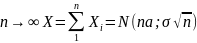
15. Пусть с испытанием связаны две случайные величины Х и Y. Будем говорить, что точка (Х,Y) – двумерная случайная величина или случайная точка Х,Y. При этом случайные величины могут быть как дискретными, так и непрерывными.
Закон распределения дискретной случайной точки задается таблицей:
В
таблице: p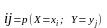
;
,
,
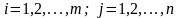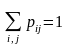Коэффициентом корреляции случайной
величины (Х,Y) называется
число
,
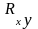равно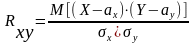е:
,
где
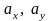– математические ожидания;
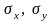– средние квадратичные отклонения
случайных величин
Х и Y
соответственно.
Ковариацией
(корреляционным моментом) случайной
величины (Х,Y)
называется число
,
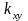равное
.
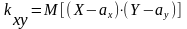Случайную точку характеризуют пять
чисел:
,
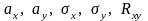где
– числовые характеристики случайной
величины Х;
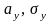– числовые характеристики случайной
величины Y;
–
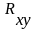коэффициент корреляции.
16)Выборка: Генеральной совокупностью называется совокупность объектов, из которых производится выборка. Выборочной совокупностью (выборкой) называется совокупность случайно отобранных объектов из генеральной совокупности. Число объектов в совокупности называется ее объемом. Выборку можно производить двумя способами. Если после исследования объект из выборки возвращается в генеральную совокупность, то такая выборка называется повторной; если объект не возвращается в генеральную совокупность, то такая выборка называется бесповторной.
Выборка называется репрезентативной (представительной), если по ее данным можно достаточно уверенно судить об интересующем признаке генеральной совокупности.
Вариационные ряды: Значения
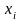называются вариантами, а их
последовательность, записанная в
возрастающем порядке, – вариационным
рядом.
Статистический ряд: Перечень вариант и соответствующих им частот называется статистическим распределением выборки
17) Эмпирическая функция распределения:
Функция
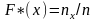, определяющая для каждого значения х
относительную частоту события
,
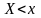называется эмпирической функцией
распределения или функцией распределения
выборки.