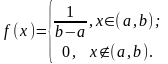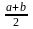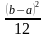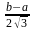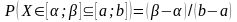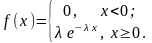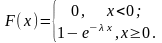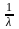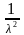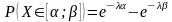- •10) Равномерное и показательное распределения нсв: функция распределения, плотность, основные параметры распределения, числовые характеристики, вероятность попадания на интервал.
- •12) Распределение χ2 Пирсона, f- распределение Фишера, t- распределение Стьюдента; основные параметры этих распределений, графики.
- •13) Неравенства Маркова и Чебышева, лемма о среднем арифметическом случ.Величин.
- •14)Закон больших чисел. Центральная предельная теорема.
- •18)Графическое представление выборки:
- •20. Точечные оценки математического ожидания и дисперсии:
- •21. Методы нахождения оценок: метод моментов
3.Свойства функции Гаусса:
1) функция четная, т.е.

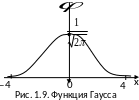 ;
;
2) функция монотонно убывает при положительных значениях х, причем
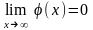 .
.
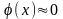 при
при
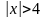 ;
;
3) площадь, заключенная между осьюОх и графиком функции Гаусса равна единице.
По определению функция Лапласа Ф(x)
– этоплощадь криволинейной трапеции,
опирающейся на отрезок [0; x],
и ограниченной сверху функцией Гаусса
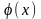 (рис.
1.10).
(рис.
1.10).
 Свойства функции Ф(x):
Свойства функции Ф(x):
Ф(x) нечетная, т. е. Ф(–x) = – Ф(x);
Ф(x) возрастает на всей числовой оси;
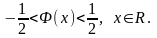
Последнее свойство следует из свойств функции Гаусса и геометрической интерпретации функции Лапласа, причем с учетом нечетности Ф(x)
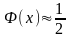 при
при
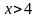 .
.
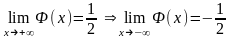
Связь - функция Гаусса является производной функции Лапласа.
5. Если с испытанием связана некоторая величина, значение которой зависит от случая, то эта величина называется случайной.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Случайная величина называется дискретной, если она принимает отдельные значения с определенной вероятностью. Число определенных значений дискретной случайной величины может быть конечным и бесконечным, но счетным. Непрерывной случайной величиной называют величину, значения которой полностью заполняют некоторый конечный или бесконечный промежуток на числовой оси.
6.
Числовые характеристики СВ:
числовые характеристики случайной
величины (математическое ожидание,
дисперсию, среднее квадратическое
отклонение и др.), которые дают некоторое
приближенное описание случайной
величины. Математическим ожиданием
дискретной случайной величины Х
называется сумма всех произведений её
возможных значений на их вероятности:
 Свойства
математического ожидания:
Свойства
математического ожидания:
1.
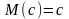 2.
2.
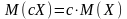 3.
3.
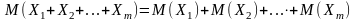
4.

Дисперсией
дискретной случайной величины Х
называется математическое ожидание
квадрата её отклонения от своего
математического ожидания:
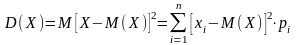
Свойства
дисперсии:1.
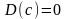 2.
2.
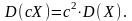 3.
3.

4.
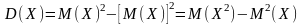 .
Средним квадратичным отклонением
случайной величины Х называется
квадратный корень из её дисперсии:
.
Средним квадратичным отклонением
случайной величины Х называется
квадратный корень из её дисперсии:
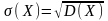
Мода: дискретной случайной величины – это ее наиболее вероятное значение. Модой непрерывной случайной величиныназывается ее значение, при котором плотность вероятности максимальна..
Медиана случайной величины Х – это варианта, которая делит вариационный ряд на 2 равные части. Ме=Хк+Хк+1/2
7. Функция
распределения интерпретируется как
вероятность того, что случайная точка
Х окажется левее заданной точки
х, т. е. попадает в интервал
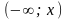 .
.

Основные свойства функции распределенияF(x):
1.
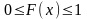
2.
F(x)
– неубыв. функция, т. е.
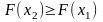 при
при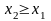
3.
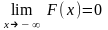 ,
т. е.
,
т. е.
 .
.
4.
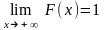 ,
т. е.
,
т. е.
 .
.
5.
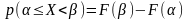 .
.
6.
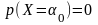
8.Биноминальный
закон распределения ДСВ:
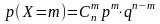 ,
где
,
где
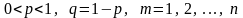 .
.
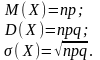
Закон
распределения Пуассона: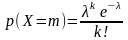 ,
,
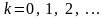 ,
где число
,
где число
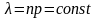 – параметр закона Пуассона.
– параметр закона Пуассона.
 .
.
Геометрический
закон распределения ДСВ: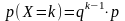 ,
где
,
где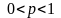 ,
,
 .
.
 .
.
9)
Плотностью
вероятности
или дифференциальной
функцией распределения
называется функция
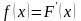 .
Плотность распределения вероятностей
f(x)
существует только для непрерывных
случайных величин, при условии, что F(x)
дифференцируема, и обладает следующими
свойствами:
.
Плотность распределения вероятностей
f(x)
существует только для непрерывных
случайных величин, при условии, что F(x)
дифференцируема, и обладает следующими
свойствами:
1. f(x)0.
2.
 3.
3.
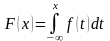 .
4.
.
4.
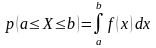 .
.
10) Равномерное и показательное распределения нсв: функция распределения, плотность, основные параметры распределения, числовые характеристики, вероятность попадания на интервал.
|
|
M(X) |
D(X) |
σ(X) |
|
Равномерный
|
|
|
|
|
Ошибка округления до ближайшего целого деления. Время ожидания транспорта с постоянным интервалом движения.
|
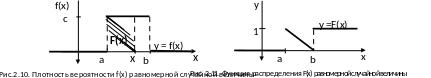
Постоянная
 ,
т. к. по свойству плотности вероятности
площадь криволинейной трапеции,
опирающейся на отрезок [a,
b],
должна быть равна 1.
,
т. к. по свойству плотности вероятности
площадь криволинейной трапеции,
опирающейся на отрезок [a,
b],
должна быть равна 1.
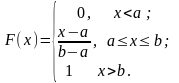 График
График
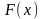 изображен на рис.
2.11.
изображен на рис.
2.11.
|
|
M(X) |
D(X) |
σ(X) |
|
П
|
|
|
|
|
Время безотказной работы прибора; продолжительность телефонного разговора
|
т.к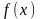 >0,
=>,
>0,
=>,
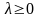 .
График
изображен на рис.
2.12.
.
График
изображен на рис.
2.12.
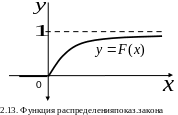
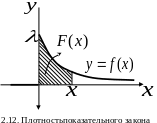
.
11.
Непрерывная случайная величина называется
нормально распределенной с
параметрами
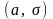 ,
если её плотность вероятности задается
формулой:
,
если её плотность вероятности задается
формулой: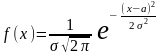
Функция распределения F(x) нормальной случайной величины
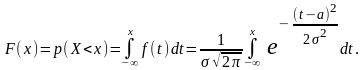
Теорема.Если
непрерывная случайная величина Х
нормально распределена c
плотностью вероятности, то её числовые
характеристики равны: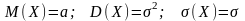
 .
.
Для нормально распределенной случайной величины Х имеют место следующие свойства.
Свойство
1. Для нормально распределенной
случайной величины с параметрами
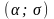 вероятность попадания на промежуток
вероятность попадания на промежуток
 вычисляется по формуле:
вычисляется по формуле:
Доказательство.По свойству плотности вероятности, свойству интеграла и равенству (2.11) имеем:
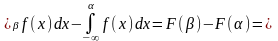
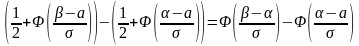
Ч.т.д
Свойство
2. Для нормально распределенной
случайной величины Х с параметрами
вероятность отклонения Х от своего
среднего значенияа меньше, чем на
 ,
вычисляется по формуле
,
вычисляется по формуле
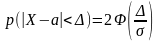 .
.
Доказательство.Используя равенство (2.12)и нечетность функции Лапласа, получаем требуемое:
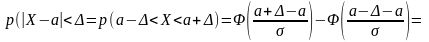
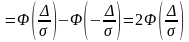
Свойство
3. Правило трех сигма.Все значения
нормально распределенной случайной
величины с практической достоверностью
лежат в интервале
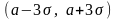 ,
т. е.
,
т. е.
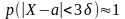
Доказательство:
Свойство
4. Пусть
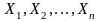 – независимые нормальные случайные
величины с параметрами
.
Тогда случайная величина
– независимые нормальные случайные
величины с параметрами
.
Тогда случайная величина
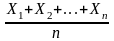 также нормально распределена и
также нормально распределена и
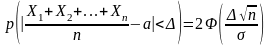
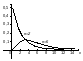
12) Распределение χ2 Пирсона, f- распределение Фишера, t- распределение Стьюдента; основные параметры этих распределений, графики.
Распределение
Пирсона (xu
– квадрат)
(xu
– квадрат)
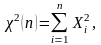 где
где
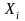 ~
~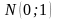
 ;
;
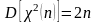
Р
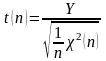 ,
где
,
где
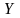 ~
~
 ;
;
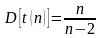
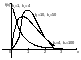
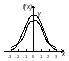
Распределение Фишера-Снедекора (F – распределение)
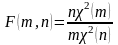 ;
;
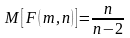
13) Неравенства Маркова и Чебышева, лемма о среднем арифметическом случ.Величин.
Неравенство Маркова:
Если Х – неотрицательная
НСВ (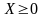 ),
тогда
),
тогда
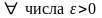 справедливо неравенство
справедливо неравенство 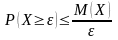 .
.
Неравенство Чебышева:
Пусть Х – СВ с числовыми
характеристиками
 и
и
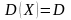 ,
тогда
справедливо неравенство
,
тогда
справедливо неравенство
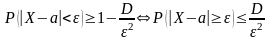 .
.
О среднем арифметическом:Если
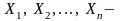 независимые
однотипные CВ с математическим
ожиданием а и дисперсией D,
тогда
независимые
однотипные CВ с математическим
ожиданием а и дисперсией D,
тогда
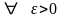 справедливо неравенство
справедливо неравенство
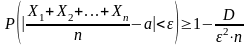 .
.