1.4.2 Количественная оценка гетероскедастичности

При малом объеме выборки, что наиболее характерно для эконометрических исследований, для оценки гетероскедастичности может использоваться метод Гольдфельда - Квандта, разработанный в 1965 г. Гольдфельд и Квандт рассмотрели однофакторную линейную модель, для которой дисперсия остатков возрастает пропорционально квадрату фактора. Чтобы оценить нарушение гомоскедастичности они предложили параметрический тест, который включает в себя следующие шаги:

1. Упорядочение n наблюдений по мере возрастания переменной x;

2. Исключение из рассмотрения С центральных наблюдений; при этом (n - C) : 2 > p, где p - число оцениваемых параметров;

3. Разделение совокупности из (n - C) наблюдений на две группы (соответственно, с малыми и с большими значениями фактора x) и определение по каждой из групп уравнений регрессии;

4. Определение остаточной суммы квадратов для первой (S₁) и второй (S₂) групп и нахождение их отношения: R = S₁ : S₂.

При выполнении нулевой гипотезы о гомоскедастичности отношение R будет удовлетворять F-критерию с (n – C - 2p) : 2 степенями свободы для каждой остаточной суммы квадратов. Чем больше величина R превышает табличное значение F-критерия, тем более нарушена предпосылка о равенстве дисперсий остаточных величин. Рассмотрим применение данного метода на следующем примере (см. табл.1.6).

Таблица 1.6

Поступление доходов в консолидированный бюджет Санкт-Петербурга (y - млрд. руб.) в зависимости от численности работающих на крупных и средних предприятиях и организациях (x - тыс. чел.) экономики районов за 1994 г⁷.

№ п/п	Районы города	xi	yi		i
1	Павловский	3	4,4	-1,0	5,4
2	Кронштадт	6	8,1	2,5	5,6
3	Ломоносовский	8	12,9	4,9	8,0
4	Курортный	18	20,8	16,6	4,2
5	Петродворец	20	15,5	19,0	-3,5
6	Пушкинский	23	28,8	22,5	6,3
7	Красносельский	39	37,5	41,4	-3,9
8	Приморский	49	48,7	53,2	-4,5
9	Колпинский	60	68,6	66,1	2,5
10	Фрунзенский	74	104,6	83,6	22,0
11	Красногвардейский	79	90,5	88,5	2,0
12	Василеостровский	95	88,3	107,4	-19,1
13	Невский	106	132,4	120,4	12,0
14	Петроградский	112	122,0	127,4	-5,4
15	Калининский	115	99,1	131,0	-31,9
16	Выборгский	125	114,2	142,7	-28,5
17	Кировский	132	150,6	151,0	-0,4
18	Московский	149	156,1	171,0	-14,9
19	Адмиралтейский	157	209,5	180,5	29,0
20	Центральный	282	342,9	327,8	15,1
Итого:		1652	1855,5	1855,5	0,0

В соответствии с уравнением (r = 0,9828, F = 510,7); найдены теоретические значения и отклонения от них фактических значений y, т.е. . Не трудно видеть, что остаточные величины _i обнаруживают тенденцию к росту по мере увеличения x и y. (См. рис. 1.16).

Э тот вывод подтверждается и по критерию Гольдфельда - Квандта. Для его применения необходимо определить сначала число исключаемых центральных наблюдений С. Из экспериментальных расчетов, проведенных авторами метода для случая одного фактора, рекомендовано при n = 30 принимать С = 8, а при n = 60, С = 16. В рассматриваемом примере при n = 20 было отобрано С = 4. Результаты расчетов представлены в табл. 1.7.

Таблица 1.7.

Проверка линейной регрессии на гетероскедастичность.

Уравнения регрессии	x	y			2
1 – я группа с первыми 8 – ю районами:	3	4,4	5,7	-1,3	1,69
	6	8,1	8,5	-0,4	0,16
	8	12,9	10,3	2,6	6,76
	18	20,8	19,6	1,2	1,44
	20	15,5	21,4	-5,9	34,81
	23	28,8	24,2	4,6	21,16
	39	37,5	38,9	-1,4	1,96
	49	48,7	48,1	0,6	0,36
Сумма					68,34
2 – я группа с последними 8 – ю районами:	106	132,4	110,7	21,7	470,89
	112	122,0	118,7	3,3	10,899
	115	99,1	122,7	-23,6	556,96
	125	114,2	136,1	-21,9	479,61
	132	150,6	145,4	5,2	27,04
	149	156,1	168,2	-12,1	146,41
	157	209,5	178,9	30,6	936,36
	282	342,9	346,1	-3,2	10,24
Сумма					2638,40

Величина R = 2638,4 : 68,34 = 19,3, что превышает табличное значение F-критерия 4,28 при 5%-ом и 8,47 при 1%-ом уровне значимости для числа степеней свободы 6 для каждой остаточной суммы квадратов ((20 4 2 * 2) : 2), подтверждая тем самым наличие гетероскедастичности.

Тест Гольдфельда – Квандта используется аналогично и при проверке на гетерокседантичность остатков множественной регрессии.

Наличие гетерокседантичности в остатках регрессии можно проверить и с помощью теста ранговой корреляции Спирмэна. Суть теста заключается в том, что в случае гетерокседантичности абсолютные остатки коррелированы со значениями фактора . Для оценки этой корреляции используется ранговый коэффициент корреляции Спирмэна:

,

где d – абсолютная разность между рангами значений и .

Для нашего примера расчет рангового коэффициента корреляции Спирмэна составит: (см. табл. 1.8)

Таблица 1.8.

Расчет рангового коэффициента корреляции Спирмэна для регрессии, представленной в табл. 3.7, т.е. между и .

№ п/п
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20	3 6 8 18 20 23 39 49 60 74 79 95 106 112 115 125 132 149 157 282	5,4 5,6 8,0 4,2 -3,5 6,3 -3,9 -4,5 2,5 22,0 2,0 -19,1 12,0 -5,4 -31,9 -28,5 -0,4 -14,9 29,0 15,1	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20	8,5 10 12 6 4 11 5 7 3 17 2 16 13 8,5 20 18 1 14 19 15	7,5 8 9 2 1 5 2 1 6 7 9 4 0 5,5 5 2 16 4 0 5	56,25 64 81 4 1 25 4 1 36 49 81 16 9 30,25 25 4 256 16 0 25
Сумма						774,5

Далее рассчитывается t – критерий как , т.е. аналогично для линейного коэффициента корреляции. В нашем случае . Сравниваем эту величину с табличным при и числа степеней свободы (n-2)=18: . Принято считать, что, если , то корреляция и существует, т.е. имеет место гетероскедастичность остатков. В противном случае принимается гипотеза об отсутствии гетероскедастичности остатков. В нашем примере фактическое и табличное значения t достаточно близки друг к другу и вероятность наличия гетероскедастичности превышает 0,9.

Рассмотренные тесты не дают количественной оценки зависимости дисперсии ошибок регрессии от соответствующих значений факторов, включенных в регрессию. Они позволяют лишь определить наличие или отсутствие гетероскедантичности остатков. Поэтому, если гетероскедантичность остатков установлена, то можно количественно оценить зависимость дисперсии ошибок. С этой целью могут быть использованы тесты Уайта, Парка, Глейзера и другие.

Тест Уайта предполагает, что дисперсия ошибок регрессии представляет собой квадратичную функцию от значений факторов, т.е. при наличии одного фактора: . Или при наличии р факторов:

Так что модель включает в себя не только значения факторов, но и их квадраты, а также попарные произведения. Поскольку каждый параметр модели должен быть рассчитан на основании достаточного числа степеней свободы, то, чем меньше объём исследуемой совокупности, тем в меньшей мере квадратичная функция сможет содержать попарные произведения факторов. Так, если регрессия строится по тридцати наблюдениям как: , то последующая квадратичная функция для остатков может быть представлена лишь как: , поскольку на каждый параметр х может приходиться не менее 6-7 наблюдений. В настоящее время тест Уайта включён в стандартную программу регрессионного анализа в пакете «Econometric Views». О наличии или отсутствии гетероскедастичности остатков судят по величине F-критерия Фишера для квадратичной функции регрессии остатков. Если фактическое значение F-критерия выше табличного, то, следовательно, существует чёткое корреляционная связь дисперсии ошибок от значений факторов, включённых в регрессию, и, стало быть, имеет место гетероскедастичность остатков. В противном случае (F_фактич<F_таблич) делается вывод об отсутствии гетероскедастичности остатков регрессии.

Применительно к нашему примеру зависимость квадратов остатков оказалась следующей:

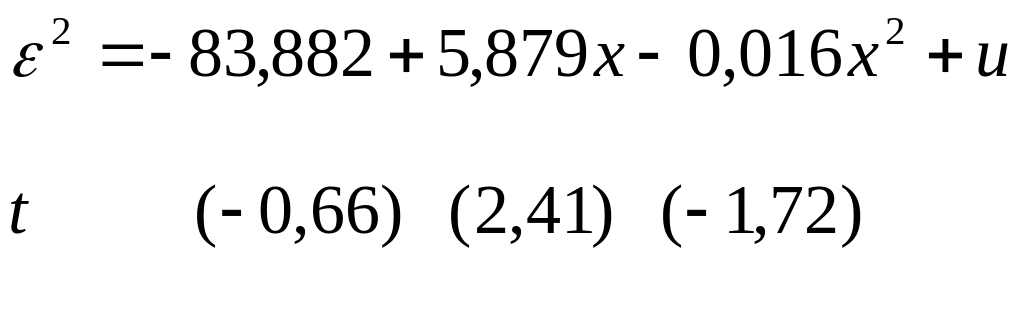
Значимость коэффициента при х весьма существенна (t_табл=2,11), коэффициент при х² менее значим: вероятность ошибки 0,1034. Но в целом F-критерий 3,77 превышает с вероятностью 0,95 табличное значении 3,59. Следовательно, необходимо признать наличие гетероскедастичности остатков, исходя из теста Уайта. При этом количественно гетероскедастичность может быть представлена квадратичной функцией.

Тест Парка также относится к формализованным тестам тестам гетероскедастичности. Предполагается, что дисперсия остатков связана со значениями факторов функций: . Данная регрессия строится для каждого фактора в условиях многофакторной модели. Проверяется значимость коэффициента регрессии «b» по t-критерию Стьюдента. Если коэффициент регрессии для уравнения окажется статистически значимым, то, следовательно, существует зависимость от lnx, т.е. имеет место гетероскедастичность остатков. В нашем примере была обнаружена квадратичная функция от х, поэтому степенная зависимость от х вряд ли будет иметь место, что и подтвердили расчеты: при табличных значениях: _0,05F_1,18=4,41 и _0,05t₁₈=2,1, т.е. дисперсия остатков не представляет собой степенную функцию от значений фактора «х».

Если тесты Уайта и Парка оценивали гетероскедастичность, строя регрессию для квадрата остатков , то тест Глейзера основывается на регрессии абсолютных значений остатков , т.е. рассматривается функция Регрессия от х_i строится при разных значениях параметра «с» и далее отбирается та функция, для которой коэффициент регрессии «b» оказывается наиболее значимым, т.е. имеет место наибольшее значение t-критерия Стьюдента или равносильно F-критерию Фишера и R². Для нашего примера тест Глейзера дал следующие результаты:

при с=1 t_b=2,306;

при с=2 t_b=1,58;

при с=3 t_b=0,956;

при с=4 t_b=0,675.

При этом «с» может принимать как дробные, так и отрицательные значения:

при с=-1 t_b=1,26;

при с=0,5 t_b=2,49;

при с=-0,5 t_b=1,71.

Абсолютная величина остатков обнаруживает некоторую гетероскедастичность при с=1 и с=0,5, когда фактические значения t_b превышает табличные 2,11.

При обнаружении гетероскедастичности остатков регрессии ставится цель её устранения, чему служит применение обобщённого метода наименьших квадратов (см. главу 4).

5 См. подробное изложение кусочно-линейных моделей "Статистическое моделирование и прогнозирование". Учебное пособие под ред. А. Г. Гранберга, М.: Финансы и статистика, 1990, с. 158.

6 Дж. Джонстон. Эконометрические методы. Пер. с англ. М.: Статистика, 1980, с. 207-241.

7 За строкой цифр. Санкт - Петербург. 1995, с.141, 155.