2.3. Метод половинного ділення

Нехай дано рівняння (2.1) : = 0.

Будемо вважати, що його корінь t відділений на відрізку [а; b]. Потрібно знайти наближене значення кореня з точністю до , де ε - досить мале позитивне число.

В основі методу половинного поділу лежить теорема про вкладенийні відрізки. Послідовність відрізків

⊃… називається вкладеною. За умови, що довжини відрізків →0 при n -> , ця послідовність називається стягающейся.

Теорема 2.4 (теорема Кантора). Для будь-якої стягующейся послідовності вкладених відрізків існує єдина точка t, що належить усім відрізкам цієї послідовностіності [3, гл. III, § 8].

Припустивши, що функція f неперервна на відрізку [а; b] і на його кінцях приймає значення різних знаків, навчимося визначать послідовність вкладених відрізків ⊂[а; b] (n == 1,2, ...), стягуються до корня t. Тим самим отримаємо метод, реалізующий перший з відмічених в 2.1 способів уточнення коренів.

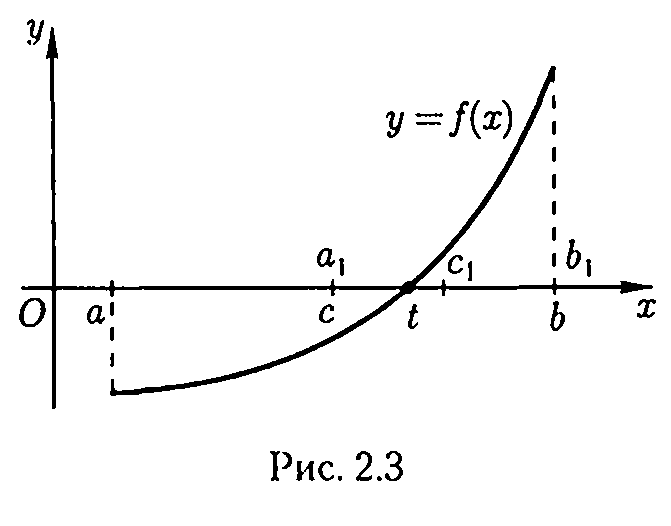
Отже, нехай f безупинна на [а; b] і . < 0 (рис. 2.3).

Розділимо [а; b] навпіл точкою с = (а + b) / 2 і обчислимо f(с).

Якщо f(с) = 0, то корінь t знайдений точно (а саме, t = с). Якщо ж ні, виберемо ту половину відрізка, на кінцях якої значення функції різних знаків, і позначимо її (на рис. 2.3 права половина [а; b]). Потім відрізок ділимо навпіл точкою і проводимо аналогічні міркування. Вийде або точний корінь , або відрізок з властивістю <0. І так далі.

Якщо на якомусь кроці виявиться точний корінь (що на практику малоймовірно), то процес поділу навпіл закінчиться, якщо ж ні, то в результаті вийде нескінченна послідовність вкладених відрізків ,…..., таких, що <0 при всіх n=1,2,… (2.4)

Зрозуміло, що Отже, отримана послідовність відрізків стягується.

Теорема Кантора гарантує існування єдиної точки, що належить усім відрізкам цієї послідовності. Так як f неперервна на [а; b], з (2.4) в силу теореми 2.1 випливає, що цією точкою є саме корінь t.

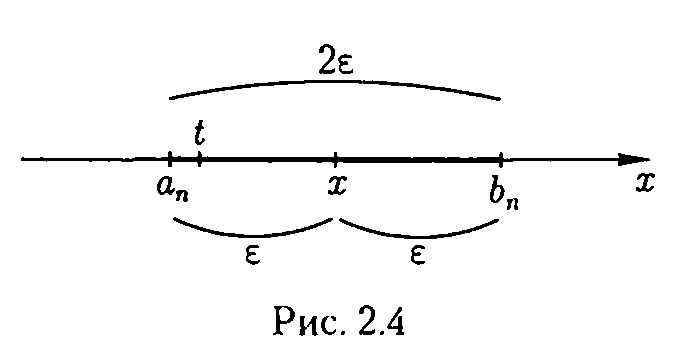
Для того щоб знайти наближене значення кореня з точністью до > 0, необхідно зупинити процес половинного ділення на такому кроці n, на якому відрізок буде мати довжину ≤2ε, (2.5)

І обчислити . Ясно, що тоді можна взяти t≈ х, причому (рис. 2.4).

Корисно мати на увазі, що обчислюється при кожному n = 1, 2, ... середінw відрізків утворюють насправді послідовноність наближень до кореня.

При цьому очевидно, що

Метод половинного ділення дає простий і зручний алгоритм уточнення коренів з будь якої наперед задано. ступенню точності. Він вимагає від функції f виконання легко перевіряючих властивостей: непереривчастості на відрізку ізоляції кореня і різних знаків значень на його кінцях.

Відмінною рисою методу є те, що швидкість наближення по ньому зовсім не пов'язана з властивостями функції в окрестності кореня. Кількість кроків наближення залежить лише від відрізка [а; b] і заданої точності ε [умова 2.5)], причому на кожному кроці абсолютна похибка наближеного значення кореня зменшується рівно вдвічі (і тільки!). Внаслідок цього збільшення точності завжди пов'язане з пропорційним зростанням обсягу обчислювальної роботи.

У правильності зроблених висновків переконують приклад 2.3 і результати упр. 2.7.

Приклад 2.3. Єдиний корінь t рівняння розташований на відрізку [1; 2] (перевірте графічно!). Для уточнення t можна застосувати метод половинного ділення, оскільки функція f: неперервна на цьому відрізку і на його кінцях приймає значення різних знаків: <0, 5> 0.

Знайдемо середину с = 1,5 відрізка [1, 2] і обчислимо значення функції f в цій точці: 0,875. Значить, число 1,5 не является точним коренем. Якщо взяти t 1,5, то / 2 = 0,5. Точність наближення невисока, але цифра 1 вже є вірною.

Далі помічаємо, що <0, > 0 і, отже, корень лежить на відрізку = [1; 1,5]. Ділимо навпіл отриманий відрізок точкою = 1,25 і знаходимо 0,3. Абсолютна похибка наближеного кореня 1,25 дорівнює 0,25. Точність підвищилася, але незначно, так як вірних цифр у наближення не додалося.

На наступному кроці треба взяти = [1,25; 1,5] і = 1,375.Оскільки , знову гарантується тільки одна вірна цифра наближеного числа 1,375. І так далі. Бачимо, що уточнення йде повільно, а для відшукання наближеного кореня з двома вірними цифрами необхідно провести ще два кроки обчислень (виконайте їх!). •

Зауваження. Якщо відрізок ізоляції кореня відомий, умова неперервності функції f перестаєбути необхідною для методу половинного ділення. Треба лише, щоб функція була визначена на цьому відрізку і брала ліворуч від кореня значення одного знака, а праворуч - іншого (упр. 2.6).