Тема 12. Теория вероятностей. Законы распределения непрерывных величин: нормальное, равномерное, показательное

1. График плотности распределения вероятностей непрерывной случайной величины Х, распределённой равномерно в интервале (-2; 6) имеет вид: 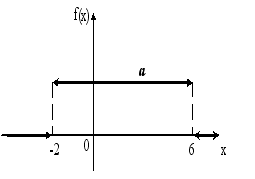Тогда значение a равно…

+a. ;

-b. ;

-c. ;

-d. .

2. Случайная величина Х распределена равномерно на отрезке [2, 5]. Распределение случайной величины Y=3X-1 имеет...

-a. другой, кроме равномерного и нормального, вид распределения;

-b. равномерное распределение на отрезке [6, 15];

+c. равномерное распределение на отрезке [5, 14];

-d. нормальное распределение на отрезке [2, 5].

3. Случайная величина Х распределена равномерно на отрезке [1, 3]. Тогда случайная величина Y=4X+1 имеет…

-a. другой (не равномерный) вид распределения;

-b. равномерное распределение на отрезке [4, 12];

-c. равномерное распределение на отрезке [2, 6];

+d. равномерное распределение на отрезке [5, 13].

4. Случайная величина Х распределена равномерно на отрезке [-3, 6]. Тогда случайная величина Y=3X-1 имеет…

-a. другой, кроме равномерного и нормального, вид распределения;

+b. равномерное распределение на отрезке [-10, 17];

-c. нормальное распределение на отрезке [-9, 18];

-d. равномерное распределение на отрезке [-8, 17].

5. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно …

+a. 4

-b. 9

-c. 18

-d. 3

6. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно …

-a. 32

+b. 5

-c. 16

-d. 4

7. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно …

+a. 7

-b. 36

-c. 72

-d. 6

8. Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей . Тогда значение С равно …

+a. 2

-b. 4

-c. − 1,75

-d. − 1

9. Непрерывная случайная величина Х задана интегральной функцией распределения вероятностей . Тогда значение С равно …

-a. 0,5

-b. 1

+c. 0

-d. 2,25

10. Случайная величина X задана плотностью распределения вероятностей: . Тогда соответствующая функция распределения вероятностей равна …

-a. ;

+b. ;

-c. ;

-d. .

11. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 4;

+b. 6;

-c. 20;

-d. 2.

12. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 32;

-b. 5;

-c. 16;

+d. 8.

13. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 2;

+b. 36;

-c. 72;

-d. 6.

14. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 4;

+b. 9;

-c. 18;

-d. 3.

15. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 32;

-b. 5;

+c. 16;

-d. 4.

16. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

+a. 10;

-b. 2;

-c. 72;

-d. 6.

17. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 2;

+b. 9;

-c. 18;

-d. 3.

18. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 32;

+b. 15;

-c. 16;

-d. 4.

19. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

+a. 17;

-b. 36;

-c. 72;

-d. 6.

20. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

+a. 14;

-b. 9;

-c. 18;

-d. 3.

21. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 32;

+b. 25;

-c. 2;

-d. 4.

22. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

+a. 12;

-b. 2;

-c. 72;

-d. 6.

23. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

+a. 24;

-b. 2;

-c. 18;

-d. 3.

24. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 32;

+b. 13;

-c. 2;

-d. 4.

25. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

+a. 1;

-b. 2;

-c. 72;

-d. 6.

26. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 14;

-b. 2;

+c. 18;

-d. 3.

27. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

-a. 32;

+b. 5;

-c. 2;

-d. 8.

28. Непрерывная случайная величина X задана плотностью распределения вероятностей .Тогда математическое ожидание этой нормально распределённой случайной величины равно…

+a. 20;

-b. 2;

-c. 72;

-d. 6.