
- •Лабораторная работа 3 исследование резонансных явлений в последовательной rlc-цепи
- •1. Цель работы
- •2. Описание схемы и экспериментальной установки
- •3. Основные теоретические положения
- •4. Задания и методические указания к выполнению работы
- •Расчетное задание
- •5. Содержание отчета
- •6. Контрольные вопросы.
Лабораторная работа 3 исследование резонансных явлений в последовательной rlc-цепи
1. Цель работы
Изучение условий возникновения резонансных явлений в последовательной RLC-цепи, определение параметров колебательного контура и проведение на ЭВМ вычислительного эксперимента получения нормированных частотных характеристик тока при разных добротностях контура.
2. Описание схемы и экспериментальной установки
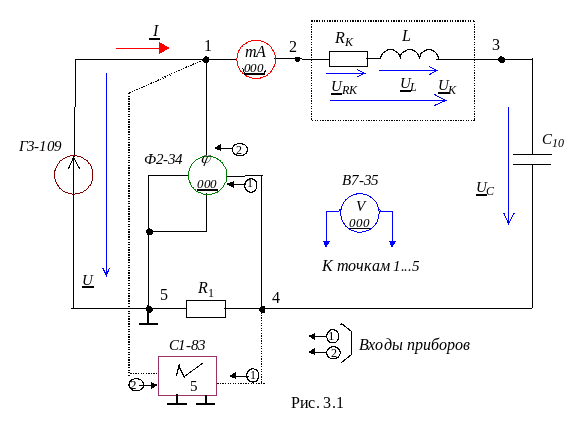
Работа проводится на учебно-исследовательском стенде ЭЛУС2. Все необходимые резистивные, индуктивные и емкостные элементы, которые требуются для сборки последовательного резонансного контура, смонтированы на панели 1. Там же приведены параметры указанных на схеме элементов.
Для выполнения эксперимента и расчетов потребуется следующая аппаратура: генератор синусоидальных колебаний Г3-109, измеритель разности фаз Ф2-34, универсальные цифровые вольтметры В7-35, микрокалькулятор, персональная ЭВМ (ПЭВМ), двухканальный осциллограф типа С1-83.
![]() и угла сдвига фаз
и угла сдвига фаз
![]() между
входным напряжением U
и током
I.
между
входным напряжением U
и током
I.
Далее, по данным экспериментов проводится на ПЭВМ вычислительный эксперимент получения нормированных частотных характеристик тока при других значениях параметров RLC-цепи, в частности при добротностях контура более 50...100, которые трудно получить при натурном эксперименте в условиях лаборатории. В то же время такие добротности являются типичными для электронных цепей повышенной избирательности.
3. Основные теоретические положения
Резонансные явления проявляют себя в электрических цепях, содержащих участки с индуктивными и емкостными элементами и фиксируются при нулевом сдвиге фаз ( = 0) между напряжением и током на входе; цепь при резонансе для источника энергии является чисто активной (резистивной) нагрузкой.
В неразветвленной RLC-цепи наблюдается резонанс напряжений, условием которого при угле = 0 является равенство нулю полного реактивного сопротивления
|
(3.1) |
где
![]() и
и
![]() -
соответственно индуктивное и емкостное
сопротивления цепи;
= 2f
- угловая частота приложенного ко входу
цепи синусоидального напряжения
-
соответственно индуктивное и емкостное
сопротивления цепи;
= 2f
- угловая частота приложенного ко входу
цепи синусоидального напряжения
![]() .
.
Решая (3.1) относительно , определяют резонансную частоту
|
(3.2) |
Ток в цепи (рис. 3.1) в отсутствие резонанса,
например, при
![]() и > 0
и > 0
|
(3.3) |
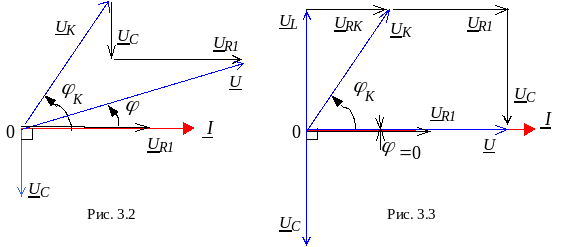
Этому режиму соответствует векторная диаграмма (рис. 3.2).
Ток в цепи при резонансе (![]() ;
;
![]() )
)
|
(3.4) |
Векторная диаграмма напряжений и тока в цепи при резонансе приведена на рис. 3.3.
![]() цепи равно индуктивному или емкостному
сопротивлению при резонансе
цепи равно индуктивному или емкостному
сопротивлению при резонансе
|
(3.5) |
а отношение напряжения на конденсаторе или напряжения на индуктивном элементе при резонансе к входному напряжению носит название добротности контура
|
(3.6) |
Добротность
показывает, во сколько раз при резонансе
напряжение на реактивном элементе (![]() или
или
![]() )
превышает входное напряжение
)
превышает входное напряжение
![]() .
В радиотехнических цепях добротность
достигает 100...300, в электротехнических
цепях - порядка 3... 5.
.
В радиотехнических цепях добротность
достигает 100...300, в электротехнических
цепях - порядка 3... 5.
Зависимость электрического
параметра
![]() и др.
и др.![]() цепи
от частоты
цепи
от частоты
![]() называют частотной
характеристикой
исследуемого параметра.
называют частотной
характеристикой
исследуемого параметра.
Построим частотную характеристику полного реактивного сопротивления RLC-цепи
|
(3.7) |
С этой целью, вначале строим
частотную характеристику индуктивного
![]() и емкостного
и емкостного
![]() сопротивлений, а затем путем суммирования
соответствующих ординат получаем
характеристику
сопротивлений, а затем путем суммирования
соответствующих ординат получаем
характеристику
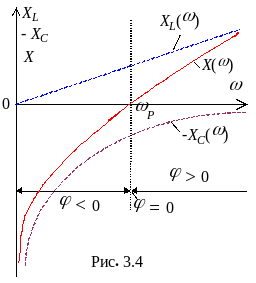
![]() (рис. 3.4). Точка пересечения характеристики
с осью абсцисс
(рис. 3.4). Точка пересечения характеристики
с осью абсцисс
![]() соответствует резонансной частоте
соответствует резонансной частоте
![]() ,
которая ограничивает области емкостного
,
которая ограничивает области емкостного
![]() и
индуктивного
и
индуктивного
![]() характеров цепи. На границе областей
цепь носит резистивный характер (
= 0).
характеров цепи. На границе областей
цепь носит резистивный характер (
= 0).
Частотную характеристику протекающего по цепи тока можно получить из соотношения (3.3), т. е.
|
(3.8) |
Поделив значение тока при любой частоте (см. выражение (3.8) на ток при резонансе (см. (3.4)), получим нормированный (относительный) ток
|
(3.9) |
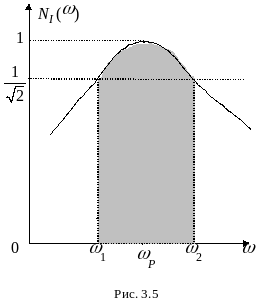
![]() представлен на рис. 3.5.
представлен на рис. 3.5.
|
(3.10) |
С учетом (3.10), соотношение (3.9) можно представить в виде
|
(3.11) |
или
|
(3.12) |
Таким образом, нормированная
частотная характеристика зависит от
резонансной частоты и добротности Q
контура (рис. 3.6). С увеличением Q
наблюдается улучшение избирательности
RLC-цепи (колебательного
контура) и уменьшается ширина полосы
пропускания
![]() ,
на границах которой (
,
на границах которой (![]() и
и
![]() ,
рис. 3.5) активная мощность Р
уменьшается в два раза, а ток снижается
до
,
рис. 3.5) активная мощность Р
уменьшается в два раза, а ток снижается
до
![]() своего максимального значения; при этом
угол
между напряжением и током на входе
контура равен
45.
своего максимального значения; при этом
угол
между напряжением и током на входе
контура равен
45.

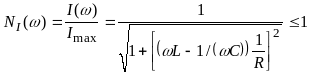 .
.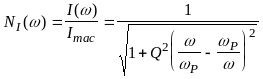 .
.