Возможные исходы лотереи
X |
Y |
X+Y |
Вероятность результата |
–1 |
–1 |
–2 |
(47/50) (46/49) = 1081/1225 |
–1 |
9 |
8 |
(47/50) (2/49) = 47/1225 |
–1 |
29 |
28 |
(47/50) (1/49) = 47/2450 |
9 |
–1 |
8 |
(2/50) (47/49) = 47/1225 |
9 |
9 |
18 |
(2/50) (1/49) = 1/1225 |
9 |
29 |
38 |
(2/50) (1/49) = 1/1225 |
29 |
–1 |
28 |
(1/50) (47/49) = 47/2450 |
29 |
9 |
38 |
(1/50) (2/49) = 1/1225 |
29 |
29 |
58 |
(1/50) (0/49) = 0 |
При нахождении вероятностей соответствующих результатов применяется теорема умножения вероятностей для зависимых событий. Например, случайная величина X+Y примет значение, равное –2 руб., если выигрыш не выпадает ни на первый, ни на второй билеты. Вероятность проиграть по первому билету лотереи равна 47/50, по второму – при условии, что первый билет не выиграл, – 46/49.
По теореме умножения получаем вероятность проигрыша по обоим билетам. Вероятность выиграть на оба билета книги по 30 руб. оказывается равной 0, так как возможен лишь один такой выигрыш. Таким образом, случайная величина X+Y может принимать следующие значения: –2, 8, 18, 28 и 38 руб.
Закон распределения случайной величины:
Сумма выигрыша, руб. |
–2 |
8 |
18 |
28 |
38 |
Вероятность |
1081/1225 |
94/1225 |
1/1225 |
47/1225 |
2/1225 |
Вероятности P(X + Y = 8), Р(Х + Y = 28) и Р(Х + Y = 38) получаем, используя теорему сложения вероятностей. Найдем математическое ожидание Х + Y:
Следовательно, М(Х + Y) = М(Х) + М(Y).
3.6. Ожидаемое среднее значение функции случайной величины
ожидаемое среднее значение можно вычислять как функцию случайной величины. Пусть h(X) – функция случайной величины X. Ожидаемое значение функции дискретной случайной величины:
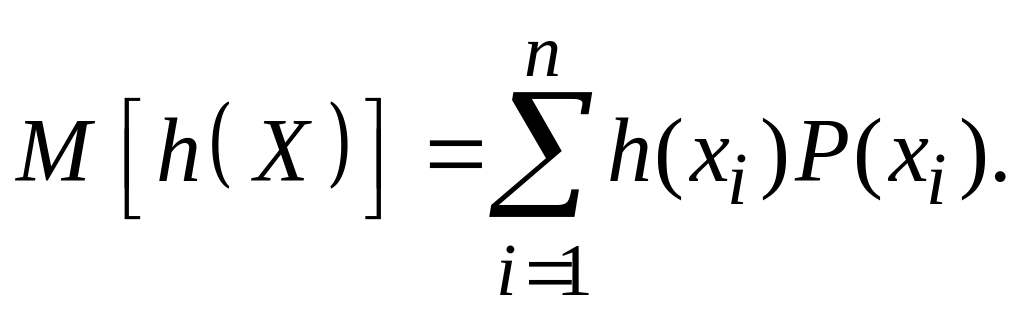(3.7)
Функция h(X) может быть любой, например X 2, 3Х 4, logX. Разберем простой пример, когда h(X) – линейная функция от X, т. е. h(X) = = аХ + b, где а, b – числовые параметры.
Пример 3.5. Компания продает некоторый продукт, учет продаж которого ведется в тысячах штук. Закон распределения объема ежемесячных продаж продукта представлен в табл. 3.5. Найдем ожидаемое среднее значение числа месячных продаж.
Таблица 3.5
Ряд распределения числа месячных продаж
Число единиц товара х, тыс, шт. |
Р(х) |
5000 6000 7000 8000 9000 |
0,2 0,3 0,2 0,2 0,1 |
|
1,0 |
Решение. Из формулы (3.4) следует, что М(Х) = 5000∙0,2 + 6000∙0,3+ + 7000∙ 0,2 + 8000∙ 0,2 + 9000∙ 0,1 = 1000 + 1800 + 1400 + + 1600 + 900 = 6700.
Пример 3.6. На данных примера 3.5 предположим, что стоимость фиксированного месячного выпуска продукции составляет 8000 условных денежных единиц, а доход от реализации каждой единицы товара – 2 денежные единицы. Найдем ожидаемый месячный доход от продажи продукции.
Решение. Функция дохода от продажи продукции компании есть h(X) = 2X – 8000. Формула (3.12) свидетельствует, что ожидаемое значение h(X) есть сумма произведений h(X) на соответствующие вероятности. Результаты расчета представлены в табл. 3.6.
Таблица 3.6