Ряд распределения случайной величины X

xi	0	1	2	3	4	5
P(xi)= pi	0,1	0,2	0,3	0,2	0,1	0,1

Поскольку появления различных значений случайной величины X – несовместные события, то вероятность того, что в газету будут помещены или 2 или 3 рекламных объявления, равна сумме вероятностей P(2) + P(3) = 0,3 + 0,2 = 0,5. Вероятность же того, что их число будет находиться в пределах от 1 до 4 (включая 1 и 4), равна 0,8, т. е. P(1 ≤ X ≤ 4) = 0,8; a P(X = 0) = 0,1. Ряд распределения можно изобразить графически. Для этого по оси абсцисс откладывают возможные значения случайной величины, а по оси ординат – соответствующие им вероятности. Если точки (x_i, p_i) соединить отрезками прямых, то полученная ломаная линия есть многоугольник (или полигон) распределения.

Рис. 3.1. Полигон распределения для данных примера 3.1

Пример 3.2. В книжном магазине организована лотерея. Разыгрываются две книги стоимостью по 10 руб. и одна – стоимостью в 30 руб. Составить закон распределения случайной величины X – суммы чистого (возможного) выигрыша для того, кто приобрел один билет за 1 руб., если всего продано 50 билетов.

Решение. Случайная величина X может принимать три значения: 1 руб. (если владелец билета не выиграет, а фактически проиграет 1 руб., уплаченный им за билет); 9 руб.; 29 руб. (фактический выигрыш уменьшается на стоимость билета – 1 руб.). Первому результату благоприятствуют 47 исходов из 50, второму – два, а третьему – один. Поэтому их вероятности таковы: P(X = –1) = 47/50 = 0,94; P(X =9) = = 2/50 = 0,04; P(X = 29) = 1/50 = 0,02;

Закон распределения случайной величины X имеет вид:

Сумма выигрыша, X	–1	9	29
Вероятность, Р	0,94	0,04	0,02

Контроль: = 0,94 + 0,04 + 0,02 = 1.

3.2. Функция распределения.

интегральная функция распределения

При анализе экономических явлений определенный смысл имеют кумулятивные (накопленные) вероятности случайных величин. Нас может интересовать вероятность того, что число проданных единиц некоторого товара окажется не меньше некоторого определенного числа, гарантирующего прибыль продавцу, вероятность того, что суммы возможных убытков от рискованных инвестиций окажутся не выше (или только меньше) некоторого определенного значения, и т. д. Зная закон распределения дискретной случайной величины, можно составить функцию накопленных вероятностей. Определим интегральную (кумулятивную) функцию распределения.

Функцией распределения дискретной случайной величины называется функция F(x), определяющая для каждого значения х вероятность того, что случайная величина X не превзойдет некоторого х, т. е.

, (3.2)

где суммирование распространяется на все значения индекса i, для которых х_i < x.

Функцию F(x) называют также накопленным (кумулятивным) распределением вероятностей. Иногда вместо термина «функция распределения» используют термин «интегральная функция распределения».

Пример 3.3. Для примера 3.1 найти функцию распределения случайной величины X – числа рекламных объявлений.

Решение. Случайная величина Х не принимает значений, меньших 0. Следовательно, если х < 0, то событие X < х невозможно, а вероятность его равна нулю. Для всех х, удовлетворяющих двойному неравенству 0 ≤ x < 1, функция F(х) означает вероятность события X < 1. Но случайная величина X принимает значение, меньшее 1, лишь в одном случае: значение 0 с вероятностью 0,1.

Покажем, что для всех х, удовлетворяющих двойному неравенству, 0 ≤ х < 2,

F(х) = 0,1 + 0,2 = 0,3.

Пусть, например, х = 2. Тогда F(2) выражает вероятность события X < 2. Это возможно в двух случаях: случайная величина X принимает значение или 0 (с вероятностью 0,1), или 1 (с вероятностью 0,2). Применив теорему сложения вероятностей, получим указанное значение функции F(х) при х = 2. Аналогичные рассуждения позволяют найти функцию распределения (табл. 3.2).

Таблица 3.2

Функция распределения (интегральная функция распределения

для примера 3.1)

x	x < 0						х  5
P(хi)	0	0,1	0,2	0,3	0,2	0,1	0,1
F(х)	0	0,1	0,3	0,6	0,8	0,9	1,0

Построим график функции распределения F(x) (рис. 3.2).

F(x)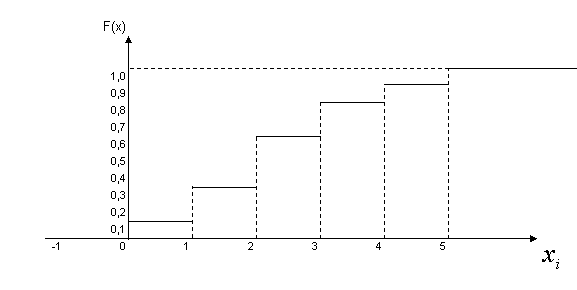

Рис. 3.2. График интегральной функции числа рекламных

объявлений

Интегральная функция – неубывающая и равна единице при х, большем наибольшего возможного значения случайной величины или равном ему (см. рис. 3.2). График F(x) имеет ступенчатый вид. Функция распределения каждой дискретной случайной величины постоянна на интервалах и имеет скачки на границах, соответствующих ее значениям. Величина скачков равна вероятностям, с которыми случайная величина принимает свои значения.

Исходя из условия примера 3.1 вероятность того, что число рекламных объявлений, помещенных в завтрашней газете, будет меньше трех, Р(Х < 3) = F(3) = 0,6. Вероятность того, что в газете будет помещено более одной рекламы, P(X > 1) = 1–F(1) =1 – 0,1 = 0,9. Вероятность того, что в газете появится от одного до трех рекламных объявлений, Р(1 ≤ Х ≤ 3) = F(4)–F(1) = 0,8 – 0,1 = 0,7.

3.3. Независимость случайных величин

и математические операции над случайными

величинами

Введем понятие независимости случайных величин. Если рассматривать не одну, а две или более случайные величины (системы случайных величин), то необходимо знать, изменяется или не изменяется закон распределения одной из них в зависимости от того, какое значение принимают другие случайные величины.

Если закон распределения одной случайной величины не зависит от того, какие возможные значения приняли другие случайные величины, то такие случайные величины называются независимыми в совокупности.

Если закон распределения одной случайной величины зависит от того, какие возможные значения приняли другие случайные величины, то такие случайные величины называются зависимыми в совокупности.

Например, приобретены два лотерейных билета различных выпусков. Пусть X – размер выигрыша по первому билету, а Y – по второму билету. Случайные величины X и Y независимы. В самом деле, если на первый билет выпал выигрыш, то закон распределения Y не изменится. Но если лотерейные билеты одного и того же выпуска, то X и Y – зависимые случайные величины.

Пусть случайная величина X принимает значения: x₁, x₂,..., х_п с вероятностями р₁, p₂,…, р_п, а случайная величина Y принимает значения у₁, у₂,…, у_т с вероятностями q₁, q₂, ..., q_т.

Определим некоторые операции над случайными величинами:

1. Произведение случайной величины X на постоянную величину С есть случайная величина СХ, которая принимает значения Сx₁, Сх₂,..., Сх_п с теми же вероятностями, что и случайная величина X.

2. Квадрат случайной величины X² – случайная величина, которая принимает свои значения х₁² , х₂² , ..., х_п² с теми же вероятностями.

3. Суммой случайных величин X и Y называется случайная величина Х+Y, возможные значения которой равны суммам каждого возможного значения X с каждым возможным значением Y, а вероятности возможных значений Х + Y для независимых величин X и Y равны произведению вероятностей слагаемых; для зависимых величин – произведениям вероятности одного слагаемого на условную вероятность второго.

4. Произведением независимых случайных величин X и Y называется случайная величина XY, возможные значения которой равны произведениям каждого возможного значения X на каждое возможное значение Y, а вероятности возможных значений произведения XY равны произведениям вероятностей возможных значений сомножителей.