Министерство сельского хозяйства Российской Федерации

Департамент научно-технологической политики и образования

ФГБОУ ВПО

КОСТРОМСКАЯ ГОСУДАРСТВЕННАЯ

СЕЛЬСКОХОЗЯЙСТВЕННАЯ АКАДЕМИЯ

Факультет заочного обучения

кафедра «Технология, организация и экономика строительства»

Контрольная работа №1

по дисциплине: «Метрология, стандартизация и сертификация»

на тему:

«___________________________________________________________________»

(указать точное наименование контрольной работы)

Дата регистрации КР в деканате ФЗО:

№________«____»_________201__г.

_______________________________

(подпись ответственного)

Дата регистрации КР на кафедре ТОиЭС:

№________«____»__________201__г.

________________________________

(подпись ответственного)

КР проверена и передана студенту для исправления:

«____»___________201__г.

Количество ошибок _____

_______________________________

(подпись преподавателя)

Дата и оценка защиты КР:

«____»___________201__г.

________________________________

(зачтено или неудовлетворительно, удовлетворительно, хорошо, отлично)

________________________________

(подпись преподавателя)

Выполнил(а) студент(ка)

_____2___группы____2______курса

факультета заочного обучения:

Спиридонова Виктория Владимировна

(Ф.И.О.)

№ зачетной книжки 103027

Кострома-2012-Караваево

Задание контрольной работы

39. Дайте понятие многократных измерений. Приведите алгоритм обработки многократных измерений.

84. Структура технического регламента.

115. Система сертификации в области пожарной безопасности: порядок проведения подтверждения соответствия.

39. Дайте понятие многократных измерений. Приведите алгоритм обработки многократных измерений.

Измерение — это совокупность операций по применению техни­ческого средства, хранящего единицу физической величины, обес­печивающих нахождение соотношения (в явном или неявном виде) измеряемой величины с ее единицей и получение значения данной величины.

Многократное измерение — измерение, результат которого получен из нескольких, сле­дующих друг за другом, измерений (т.е. состоящее из ряда од­нократных измерений).

Обработка результатов прямых многократных измерений

Методика получения результатов при проведении многократ­ных прямых измерений установлена ГОСТ 8.207—76 «ГСИ. Пря­мые измерения с многократными наблюдениями. Методы обра­ботки результатов наблюдения. Основные положения». Перед рассмотрением методики напомним, что ГОСТ 8.207 разработан и утвержден в период действия ныне отмененных ГОСТ 16263 на термины и определения в области метрологии, ГОСТ ов се­рии «П.», устанавливающих правила математической стати­стики при определении закона распределения, и отсутствия каких бы то ни было представлений о неопределенности ре­зультатов измерений.

Основные операции и их последовательность Методика обра­ботки результатов прямых многократных измерений включает в себя следующие операции:

• определение наличия грубых погрешностей и исключение промахов;

• исключение известных систематических погрешностей из результатов наблюдений;

• вычисление среднего арифметического исправленных ре­зультатов наблюдений, принимаемого за результат изме­рения;

• вычисление оценки среднего квадратического отклонения результата наблюдений;

• вычисление оценки среднего квадратического отклонения результата измерения;

• проверку гипотезы о том, что результаты наблюдений принадлежат нормальному распределению. Проверку ги­потезы о том, что результаты наблюдений принадлежат

нормальному распределению, следует проводить с уровнем значимости q от 10 до 2%. Конкретные значения уровней значимости должны быть указаны в конкретной методике выполнения измерений;

• вычисление доверительных границ случайной погрешно­сти (случайной составляющей погрешности) результата измерения;

• вычисление границ неисключенной систематической по­грешности (неисключенных остатков систематической по­грешности) результата измерения;

• вычисление доверительных границ погрешности результата измерения. Для определения доверительных границ по­грешности результата измерения доверительную вероят­ность Р, как правило, принимают равной 0,95. В тех слу­чаях, когда измерение нельзя повторить, помимо границ, соответствующих доверительной вероятности Р = 0,95, до­пускается указывать границы для доверительной вероятно­сти Р = 0,99. В особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо Р = 0,99 принимать более высокую до­верительную вероятность.

Подготовка результатов наблюдений к обработке Способы обнаружения грубых погрешностей должны быть указаны в методике выполнения измерений. Важное значение при опре­делении наличия грубых погрешностей имеет вопрос о законе распределения результатов измерений. Как правило, результа­ты измерений считают принадлежащими к нормальному рас­пределению. Для нормального распределения разработано не­сколько критериев оценки наличия грубых погрешностей. В целом их действие основано на представлении о том, что из­меряемая величина может характеризоваться большим коли­чеством измерительной информации (генеральной выборкой) и ее ограниченным количеством (выборкой). Результаты об­работки будут тем точнее, чем на больший объем информа­ции они опираются. Поэтому критерии отнесения погрешно­стей к грубым можно разделить на критерии сопоставления имеющихся результатов с характеристиками генеральной вы­борки и характеристиками распределения собственно полу­ченных результатов.

Если известны характеристики генеральной выборки (сред­нее квадратическое отклонение) или они могут быть получены в результате обработки предшествующих опытов, то следует пользоваться критериями, основанными на известном гене­ральном среднем квадратическом отклонении, и только когда оно неизвестно и нет возможности его получить, следует поль­зоваться критериями, основанными на использовании выбо­рочного среднего квадратического отклонения. Так как грубые погрешности способны заметно повлиять на результат измере­ния, рассмотрим некоторые, наиболее употребляемые из из­вестных критериев.

1. Значение генерального среднего квадратического отклонения неизвестно.

В таком случае имеются результаты наблюдений, составляю­щие упорядоченную выборку, которую можно представить в виде:

(1)

Сомнению могут быть подвергнуты, естественно, результаты, заметно отличающиеся по величине от остальных, т.е. либо наименьший (Х₁), либо наибольший (Х_n).

Среднее арифметическое значение выборки [Хи Х_п] составит:

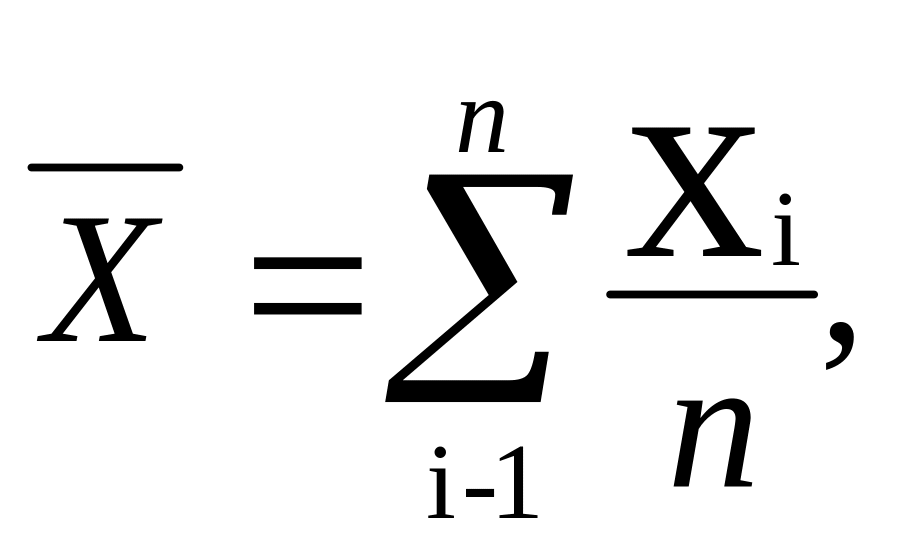(2)

а среднее квадратическое отклонение:

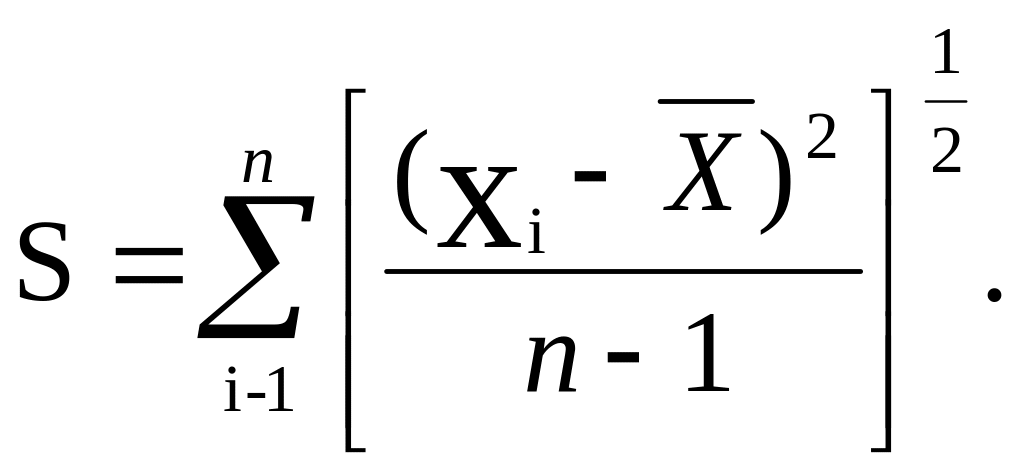(3)

Принадлежность х_{1 или} х_п к данной выборке, распределен­ной по нормальному закону, определяется по значению соот­ношений:

или . (4)

Если значения U_n или U₁ превысят критические значения р, приведенные в табл. 1, то соответствующий результат не при­надлежит нормальному распределению и из результатов измере­ний должен быть исключен.

Таблица 1. Предельные значения β для случая неизвестного генерального среднего квадратического отклонения

Объем выборки, n	Предельное значение β при уровне значимости α
	α = 0,100	α = 0,075	α = 0,050	α = 0,025
3	1,15	1,15	1,15	1,15
4	1,42	1,44	1,46	1,48
5	1,60	1,64	1,67	1,72
6	1,73	1,77	1,82	1,89
7	1,83	1,88	1,94	2,02
8	1,91	1,96	2,03	2,13
9	1,98	2,04	2,11	2,21
10	2,03	2,10	2,18	2,29
11	2,09	2,14	2,23	2,36
12	2,13	2,20	2,29	2,41
13	2,17	2,24	2,33	2,47
14	2,21	2,28	2,37	2,50
15	2,25	2,32	2,41	2,55
16	2,28	2,35	2,44	2,57
17	2,31	2,38	2,48	2,62
18	2,34	2,41	2,50	2,66
19	2,36	2,44	2,52	2,68
20	2,38	2,46	2,56	2,71

2. Значение генерального среднего квадратического отклонения известно. Значение генерального среднего арифметического неиз­вестно.

Практика измерений столь обширна, что довольно часто встречается ситуация, когда из предшествующих опытов значе­ние генерального среднего квадратического (обозначим его а Для различия со средним квадратическим выборки S) известно, а генеральное среднее арифметическое — нет. В этом случае со­ставляют упорядоченную выборку (1) и подсчитывают сред­нее арифметическое (2). По полученным данным подсчиты­вают значения коэффициентов:

или (5)

Если полученные значения превысят критические значения β, приведенные в табл. 2, то соответствующие результаты анор­мальны и из полученного ряда измерений должны быть ис­ключены.

Таблица 2. Предельные значения р для случая известного значения генерального среднего квадратического отклонения и неизвестного значения генерального среднего арифметического

Объем выборки, n	Предельное значение β при уровне значимости α
	α = 0,100	α = 0,075	α = 0,050	α = 0,025
3	1,497	1,738	2,215	2,396
4	1,696	1,941	2,431	2,618
5	1,835	2,080	2,574	2,764
6	1,939	2,184	2,679	2,870
7	2,022	2,267	2,761	2,952
8	2,091	2,334	2,828	3,019
9	2,150	2,392	2,884	3,074
10	2,200	2,441	2,931	3,122
11	2,245	2,484	2,973	3,163
12	2,284	2,523	3,010	3,199
13	2,320	2,557	3,043	3,232
14	2,352	2,589	3,072	3,261
15	2,382	2,617	3,099	3,287
16	2,409	2,644	3,124	3,312
17	2,434	2,668	3,147	3,334
18	2,458	2,691	3,158	3,365
19	2,480	2,712	3,188	3,375
20	2,500	2,732	3,207	3,393
21	2,519	2,750	3,224	3,409
22	2,538	2,768	3,240	3,425
23	2,555	2,784	3,255	3,439
24	2,571	2,800	3,269	3,453

3. Значение генерального среднего квадратического отклонения из­вестно. Значение генерального среднего арифметического известно.

Этот случай довольно часто встречается на практике при контроле постоянно протекающих процессов (транспортировка газа, жидкости и т.п.). Проверка принадлежности к нормально­му распределению для этих условий возможна даже для выбор­ки, состоящей из одного члена. Предположим, что выборка упо­рядочена и представлена в виде (1). Значение генерального среднего арифметического обозначим а. Рассчитаем значения:

или (6)

Если какое-то значение, полученное по зависимостям (5) будет больше критических значений β, приведенных в табл. 3, то соответствующий результат должен быть исключен.

Таблица 3. Предельные значения β для случая известных значений генерального среднего арифметического и генерального среднего квадратического

Объем выборки, n	Предельное значение β при уровне значимости α
	α = 0,100	α = 0,050	α = 0,0010	α = 0,005	α = 0,001
1	1,282	1,645	2,326	2,576	3,090
2	1,632	1,955	2,575	2,807	3,290
3	1,818	2,121	2,712	2,935	3,403
4	1,943	2,234	2,806	3,023	3,481
5	2,036	2,319	2,877	3,090	3,540
6	2,111	2,386	2,934	3,143	3,588
7	2,172	2,442	2,981	3,188	3,628
8	2,224	2,490	3,022	3,227	3,662
9	2,269	2,531	3,057	3,260	3,692
10	2,309	2,568	3,089	3,290	3,719
15	2,457	2,705	3,207	3,402	3,820
20	2,559	2,799	3,289	3,480	3,890
25	2,635	2,870	3,351	3,539	3,944
30	2,696	2,928	3,402	3,587	3,988
40	2,792	3,015	3,480	3,662	4,054
50	2,860	3,082	3,541	3,716	4,108
100	3,076	3,285	3,723	3,892	4,263
250	3,339	3,534	3,946	4,108	4,465
300	3,528	3,703	4,108	4,263	4,607

После оценки наличия грубых погрешностей и исключения содержащих их результатов производят оценку наличия система­тических погрешностей и внесение поправок в результаты измерений. Если во всех результатах содержится постоянная систематическая погрешность, то допускается исключать ее после вычисления среднего арифметического неисправленных резуль­татов наблюдений.

Определение результата измерения и оценка его среднего квадратического отклонения. За результат измерения принимают среднее арифметическое результатов наблюдений, в которые предварительно введены поправки для исключения системати­ческих погрешностей.

Несмещенной оценкой генерального среднего арифметиче­ского значения исправленных результатов наблюдений (а) нор­мального распределения является выборочное среднее X, опре­деляемое по формуле (2). Несмещенная оценка (Si) для гене­рального среднего квадратического отклонения (α) определяет­ся по зависимости:

(7)

Где ­- коэффициент, значения которого приведены в таблице 4;

S – среднее квадратичное отклонение выборки, рассчитываемое по зависимостям:

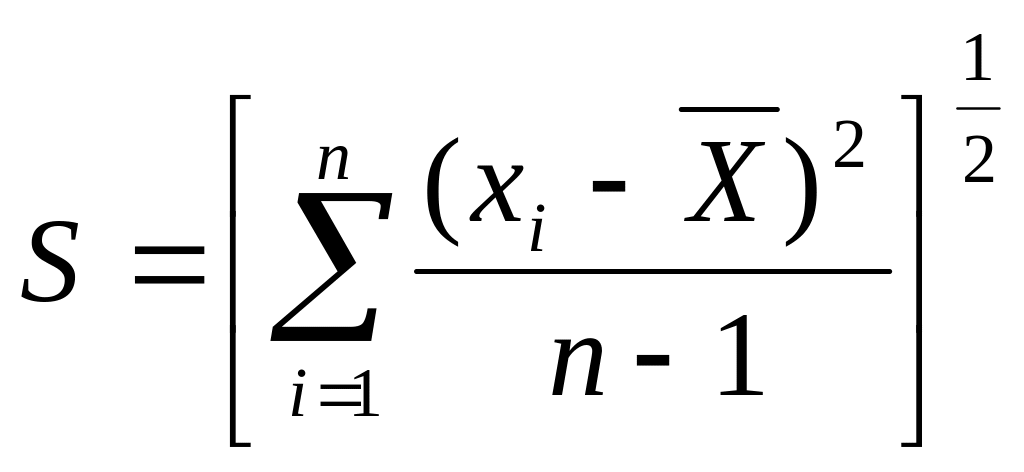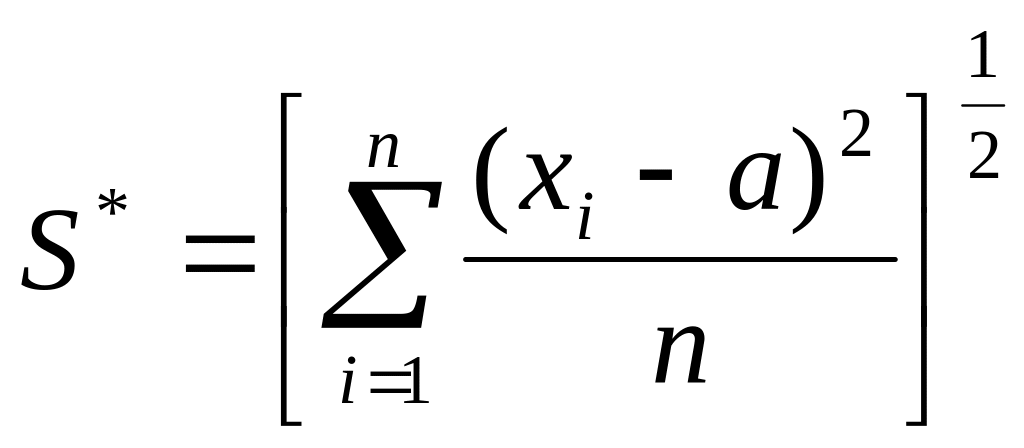или (8)

К – параметр; при известном значении a K = n, и К = n – 1 при неизвестном a (вместо a используется значение X).

Таблица 4. Значения коэффициентов .

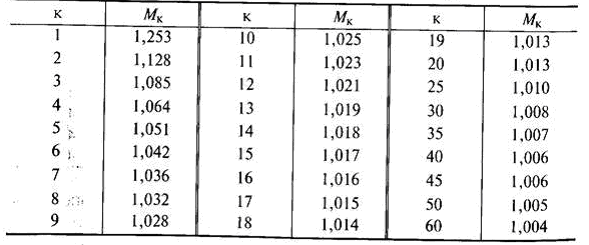
Зависимости (7) и (8) позволяют оценить среднее квадратическое отклонение результата наблюдения.

Среднее квадратическое отклонение S(A) результата измере­ния оценивают по формуле:

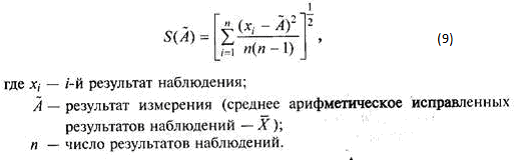
Доверительные границы случайной погрешности результата измерения ГОСТ 8.207 установил методику оценки довери­тельных границ случайной погрешности результата измерения для результатов наблюдений, принадлежащих нормальному распределению. Если это условие не выполняется, то методы вычисления доверительных границ случайной погрешности должны быть указаны в методике выполнения конкретных измерений.

Принадлежность результатов наблюдений к нормальному распределению проверяют с помощью специальных критериев.

Если число результатов наблюдений п > 50, то для проверки принадлежности их к нормальному распределению предпочти­тельно использовать один из критериев: χ² Пирсона или ω² Мизеса — Смирнова.

1. Критерий χ² Пирсона. Результаты наблюдений случайной величины x_i располагают в порядке возрастания (1) и вычис­ляют размах х_п — х₁. Размах разбивают на г равных интервалов шириной h:

Число интервалов r выбирают в зависимости от объема вы­борки п. При п = 200 r = 18—20, при п = 400 r = 25—30, при п = 1000 r=— 35—40. Стандарт не рекомендует использовать кри­терий Пирсона при числе наблюдений меньше 200, допуская в исключительных случаях его применение при 100 < п < 200 с количеством интервалов r = 15—18. Однако в работе [10] приво­дятся несколько иные рекомендации. Так, при числе наблюде­ний 50 < п≤ 100 рекомендуемое число интервалов r = 7—9, при 100 < п ≤ 500 r = 8—12, при 500 < n ≤1000 r = 10—16 и при 1000 < п ≤ 10 000 r = 12—22.

Результаты наблюдений группируют по полученным интер­валам и подсчитывают частоты m_j попадания результатов на­блюдений в j-е интервалы.

Затем вычисляются среднее арифметическое значение X и среднее квадратическое отклонение S:

Задаются значением доверительной вероятности того, что величина χ², полученная вследствие случайных отклонений частостей опытного распределения от соответствующих вероятно­стей теоретического распределения, будет меньше значения

(χ *)², установленного для значения доверительной вероятности γ. Для доверительной вероятности γ и числа степеней свободы k = r — 1 находят величину (χ*)²/k, вычисляют (χ*)² и сравнивают с ним вычисленную величину χ². Если χ² окажется меньше (χ*)², то для принятой доверительной вероятности гипотеза о согласии опытного и теоретического распределений принимается, в про­тивном случае — отвергается.

2. Критерий ω² Мизеса — Смирнова. Критерий ω² является более мощным, чем критерий χ², но его применение требует выполнения большого количества вычислительных операций. Критерий ω² может быть применен, если число наблюдений превышает 50. Его применение является обязательным, если число наблюдений меньше 200; если число наблюдений более 200, то его применение рекомендуется в случаях, когда результа­ты проверки по другим критериям не позволяют сделать безус­ловный вывод о согласии опытного и теоретического распреде­лений. Например, если при проверке согласия по критерию χ² гипотеза принята при уровне значимости 0,1 и отвергнута при уровне значимости 0,05, то следует дополнительно применить критерий ω².

Вычисление по критерию ω² проводят в следующем порядке.

Вычисляют значение величины по формуле:

Если число результатов наблюдений 50 > п > 15, то для про­верки принадлежности их к нормальному распределению пред­почтительно использовать составной критерий.

2. Составной критерий. Критерий 1. Вычисляют отно­шение d по формуле:

3. 

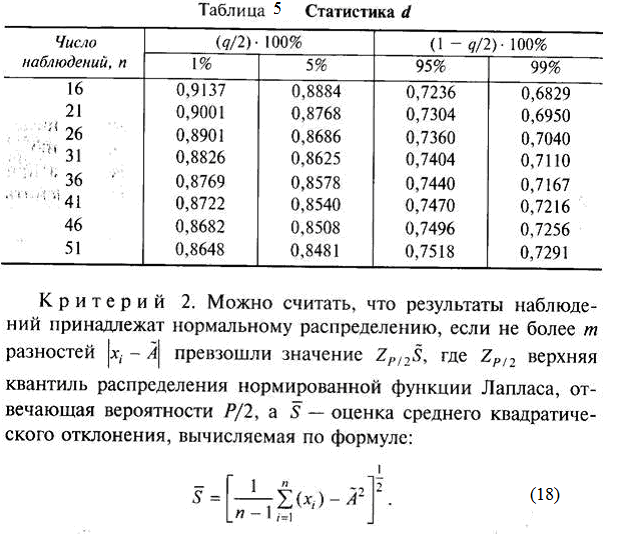
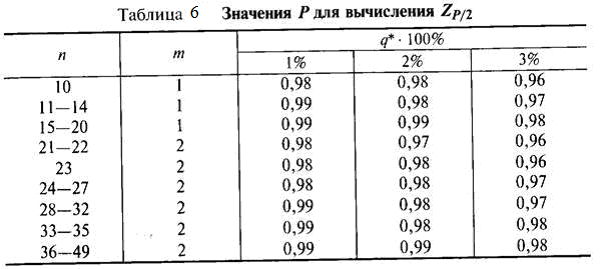
Значения Р определяются из табл. 6 по выбранному уров­ню значимости q* и числа результатов наблюдений п.

При уровне значимости, отличном от представленных в табл. 6, значение Р находят путем линейной интерполяции.

В случае если при проверке нормальности распределения результатов наблюдений группы для критерия 1 выбран уро­вень значимости q, а для критерия 2 — уровень значимости q*, то результирующий уровень значимости составного критерия q_Σ<q + q* .

В случае если хотя бы один из критериев не соблюдается, то считают, что распределение результатов наблюдений группы не соответствует нормальному.

Если число результатов наблюдений n≤ 15, то принадлеж­ность их к нормальному распределению не проверяют. Нахож­дение доверительных границ случайной погрешности результата измерения по рассматриваемой нами методике возможно только в том случае, если заранее известно, что результаты наблюдений принадлежат нормальному распределению.

Доверительные границы ε (без учета знака) случайной по­грешности результата измерения находят по формуле:

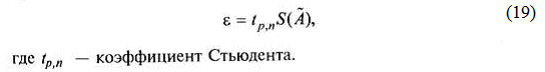
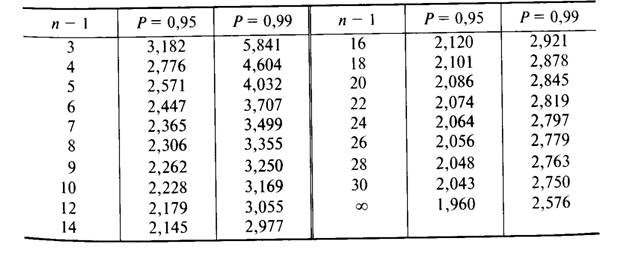
Значения коэффициента Стьюдента в зависимости от зада­ваемых значений доверительной вероятности Р и числа резуль­татов наблюдений п приведены в табл. 7.

Таблица 7. Значения коэффициента t_p,n для случайной величины, имеющей распределение Стьюдента с n - 1 степенями свободы

Доверительные границы неисключенной систематической по­грешности результата измерения Не исключенная систематиче­ская погрешность результата измерения образуется из состав­ляющих, в качестве которых могут быть рассмотрены неисключенные систематические погрешности метода измерения, средств измерений или вызванные другими источниками.

В качестве границ составляющих неисключенной систематиче­ской погрешности принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.

При суммировании составляющих неисключенной система­тической погрешности результата измерения неисключенные систематические погрешности средств измерений каждого типа и погрешности поправок рассматривают как случайные величи­ны. При отсутствии данных о виде распределения случайных величин их распределения принимают за равномерные.

Границы неисключенной систематической погрешности 0 результата измерения вычисляют путем построения композиции неисключенных систематических погрешностей средств измере­ний, метода измерения и погрешностей, вызванных другими источниками. При равномерном распределении неисключенных систематических погрешностей эти границы (без учета знака) можно вычислить по формуле:

При трех или четырех слагаемых Θ_i в качестве значения Θ₁ принимают составляющую, по числовому значению наиболее отличающуюся от других, а в качестве Θ₂ — ближайшую по зна­чению к Θ₁ составляющую.

Доверительную вероятность для вычисления границ неис­ключенной систематической погрешности принимают той же, что и при вычислении доверительных границ случайной по­грешности результата измерения.

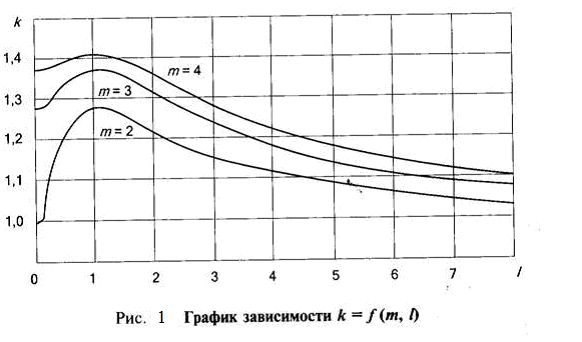
Граница погрешности результата измерения Методика оценки границ погрешности результата измерения зависит от соотно­шения значений случайной и неисключенной систематической составляющих, рассмотренных нами выше. Выделяют три воз­можных случая.

1. Неисключенной систематической составляющей погреш­ности результата измерения можно пренебречь. Необходимым условием для этого является соблюдение неравенства:

На основе (22) принимают, что граница погрешности ре­зультата измерения ∆ = ε.

2. Случайной составляющей погрешности результата измере­ния можно пренебречь. Необходимым условием для этого явля­ется соблюдение неравенства:

На основе (23) принимают, что граница погрешности ре­зультата измерения ∆= Θ.

При выполнении условий 1 и 2 погрешность оценки вели­чины ∆ за счет пренебрежения значением случайной или неисключенной систематической составляющих не превышает 15%.

3. В случае если неравенства (22) или (23) не выполняют­ся, границу погрешности результата измерения находят путем построения композиции распределений случайных и неисклю-ченных систематических погрешностей, рассматриваемых в дан­ном случае. Если доверительные границы случайных погрешно­стей найдены в соответствии с (19), то допускается границы погрешности результата измерения ∆ (без учета знака) вычис­лять по формуле:

Форма записи результатов измерений При оформлении резуль­татов измерений следует пользоваться рекомендациями МИ 1317.

Если доверительные границы погрешности результата измерения симметричны, то результаты измерений представляют в форме:

Числовое значение результата измерения должно оканчи­ваться цифрой того же разряда, что и значение погрешности ∆ .

Если данные о виде функций распределений составляющих погрешности результата измерения и необходимость в дальней­шей обработке результатов или анализе погрешностей отсутст­вуют, результаты измерений представляют в форме:

В случае если границы неисключенной систематической по­грешности 0 вычислены в соответствии с (20), следует дополни­тельно указывать доверительную вероятность Р. Значения S(A) и Θ могут быть выражены в абсолютной и относительной формах.