
- •Розрахунок річного стоку заданої забезпеченості
- •Розрахунок норми річного стоку при наявності даних спостережень
- •Метод найбільшої правдоподібності
- •Метод моментів
- •Розрахунок норми річного стоку при відсутності даних спостережень
- •Розрахунку норми річного стоку річка Південний Буг пункт Сабаров при наявності даних спостережень
- •Визначення коефіцієнта варіації сv і асиметрії Cs
- •Обчислення статистичних параметрів річного стоку річка Південний Буг пункт Сабаров
- •Розрахунок річного стоку заданої забезпеченості
- •Приклад розрахунку річного стоку заданої забезпеченості річка Південний Буг пункт Сабаров
- •Координати теоретичної кривої забезпеченості
Розрахунок норми річного стоку при наявності даних спостережень
Розрахунок річного стоку заданої забезпеченості
Розрахунок норми річного стоку при наявності даних спостережень
Однією з найважливіших гідрологічних характеристик, яку враховують при проектуванні гідротехнічних споруд, водосховищ, водопостачання, осушувальних і зрошувальних систем, є норма річного стоку, яка визначає потенційні водні ресурси даного району або басейну.
Нормою річного стоку називають середню величину річного стоку за багаторічний період, який включає в себе не менше двох повних циклів водності при відносно незмінних фізико-географічних умовах та рівневі господарської діяльності в басейні.
Аналіз ряду даних на циклічність здійснюють за допомогою різницевих інтегральних кривих, які є послідовною сумою відхилень модульних коефіцієнтів від середнього значення, що дорівнює одиниці [3].
Якщо тривалість спостережень за стоком перевищує 50-60 років, то аналіз на циклічність не проводять, а включають весь період спостережень.
При наявності матеріалів спостережені, за стоком, норму річного стоку визначають як середню арефметичну величину річного стоку
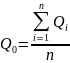 ,
(1)
,
(1)
де Qo - середня багаторічна витрата води; Qi - середньорічні витрати води за окремі роки; п - кількість років спостереження за стоком.
Розраховану величину Q0 річного стоку приймають за норму тоді, коли відносна середня похибка її обчислення не перевищує 10%. Якщо відносна середня похибка більша 10% то розрахунок Q0 ведемо як при короткому ряді спостережень.
Відносну середню похибку обчислюють за формулою
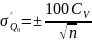 ,
(2)
,
(2)
де CV - коефіцієнт варіації стоку,
Коефіцієнт варіації СV та асиметрії CS річного стоку визначають або методом моментів (при CV < 0,5), або методом найбільшої правдоподібності (при CV > 0,5).
Метод найбільшої правдоподібності
Розрахунковий коефіцієнт варіації СV і коефіцієнт асиметрії CS для трипараметричного гама-розподілу методом найбільшої правдоподібності визначається за номограмами в залежності від статистик λ2 і λ3, котрі обчислюються за формулами
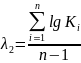 ,
(3)
,
(3)
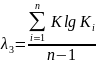 , (4)
, (4)
В наведених формулах К, - модульний коефіцієнт, що визначається за співвідношенням
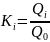 ,
(5)
,
(5)
де Qi - щорічні значення річних витрат води; Q0 - середнє арифметичне значення річних витрат води за п років.
Оцінка точності розрахунку коефіцієнта варіації методом найбільшої правдоподібності здійснюється за формулою
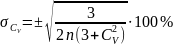 ,
(6)
,
(6)
де
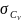 -
відносна
середньоквадратична похибка.
-
відносна
середньоквадратична похибка.
Тривалість ряду вважають достатньою, якщо не перевищує 10%.
Метод моментів
Статистичні параметри Cv і Cs - кожного значення в даному випадку розраховуються за формулами
 ;
(7)
;
(7)
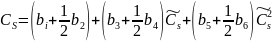 ;
(8)
;
(8)
де Cv і Cs - зміщені коефіцієнти варіації і асиметрії; а1 ... а6; b1 ... b6 - коефіцієнти, які визначають за обов'язковими додатками 2 і 3 "СНиП 2.01.14-83" і залежать від співвідношення між коефіцієнтами асиметрії та варіації і коефіцієнта автокореляції між суміжними членами ряду.
Для рядів із незначною мінливістю річного стоку, а також зміщені коефіцієнти варіації і асиметрії обчислюються за формулами
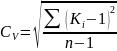 ,
при
,
при
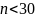 ;
(9)
;
(9)
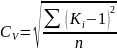 ,
при
,
при
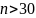 ;
(10)
;
(10)
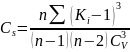 ,
(11)
,
(11)
Оцінка точності обчислення СV і Cs в цьому випадку здійснюється за формулами
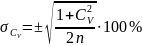 ,
(12)
,
(12)
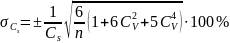 (13)
(13)
