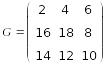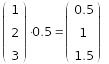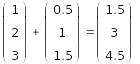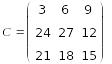Лабораторная работа №2. Числовые массивы. Матрицы

Массивы — упорядоченные последовательности чисел или строк, которые называются элементами.

Доступ к любому элементу массива возможен по его индексу, т.е. номеру в последовательности чисел. Над элементами матрицы можно производить обычные вычисления, задав соответствующие индексы.

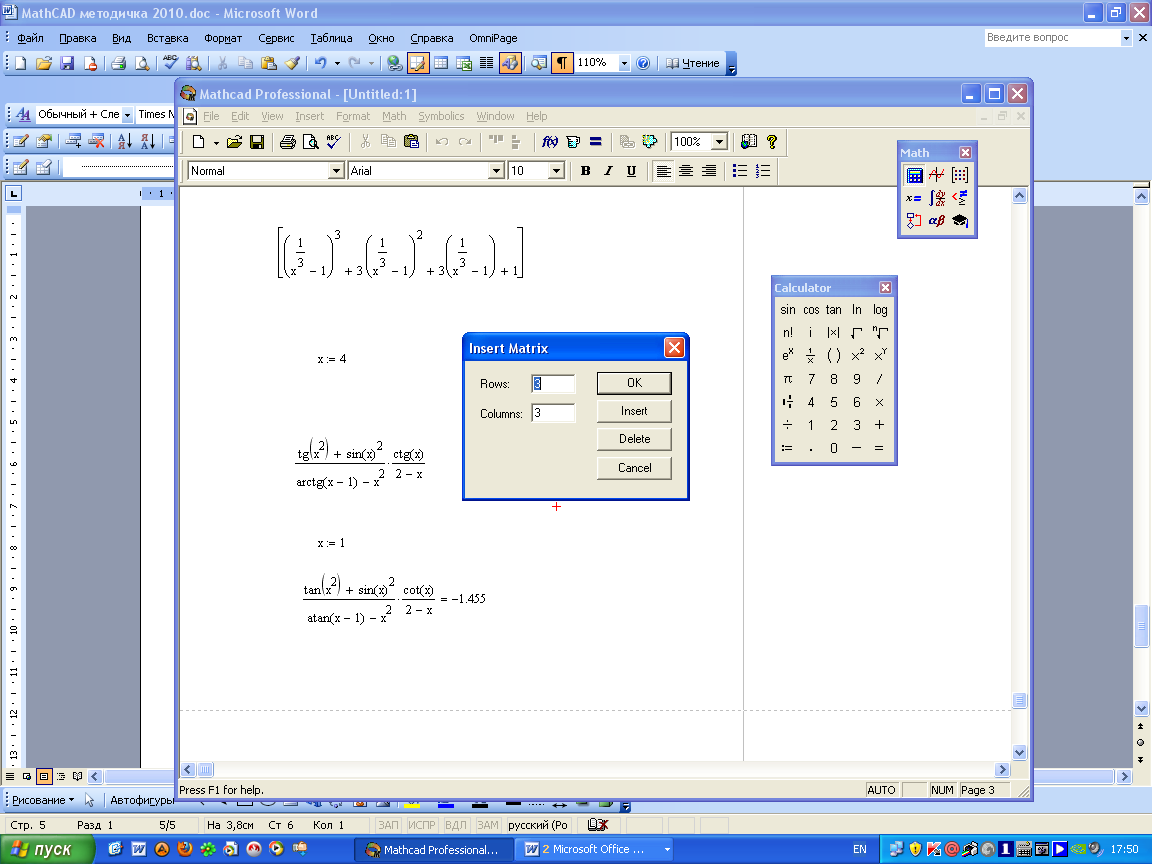
Создаются матрицы при помощи кнопки палитры инструментов или команды меню (Вставка –Матрица…) Insert- Matrix... (Ctrl+M), где указывается количество строк, столбцов (Rows и Columns).

Для примера создадим матрицу размером 3*3 и 3*1:

Матрицу с одним столбцом называют вектор-столбец. Матрицу с одной строкой называют вектор-строка.

Принято обозначать матрицы большими латинскими буквами.

С матрицами можно проделывать множество операций, имеется даже специальная матричная алгебра, но это выходит за рамки нашего курса и мы ограничимся лишь обычными операциями с массивом чисел:

1. Умножение матрицы на число.
2. Сложение матриц.

Примечание. Совершенно очевидно, что в операциях сложения размеры матриц должны совпадать.

Доступ к элементам матриц

Имея дело с массивами чисел, неплохо было бы иметь возможность извлечения отдельного числа из матрицы. Для этого реализован механизм индексирования. Так в одномерной матрице (вектор-столбце) все значения пронумерованы от 0 до n-1, где n - количество значений.

Обращение к элементу массива прозводится по индексу. Например, в матрице В три значения с индексами 0,1,2 и обращение к ним производится, как к переменной с индексом:

Индекс вводится символом квадратной скобки [ - B[0, B[1, B[2 или из кнопкой из панели .

Примечание. Переменная с индексом может присутствовать в арифметическом выражении наряду с другими переменными.

Обращение к двумерному массиву производится аналогично, только приходится указывать два индекса через запятую: первый индекс - это номер строки, второй - номер столбца. Как и ранее нумерация начинается с 0. Например:

Примечание. По умолчанию нумерация индексов начинается с нуля! Это можно изменить с помощью специальной системной переменной (ORIGIN).

Примечание. В векторе-строке необходимо все равно указывать 2 индекса, в качестве первого указывается цифра 0!

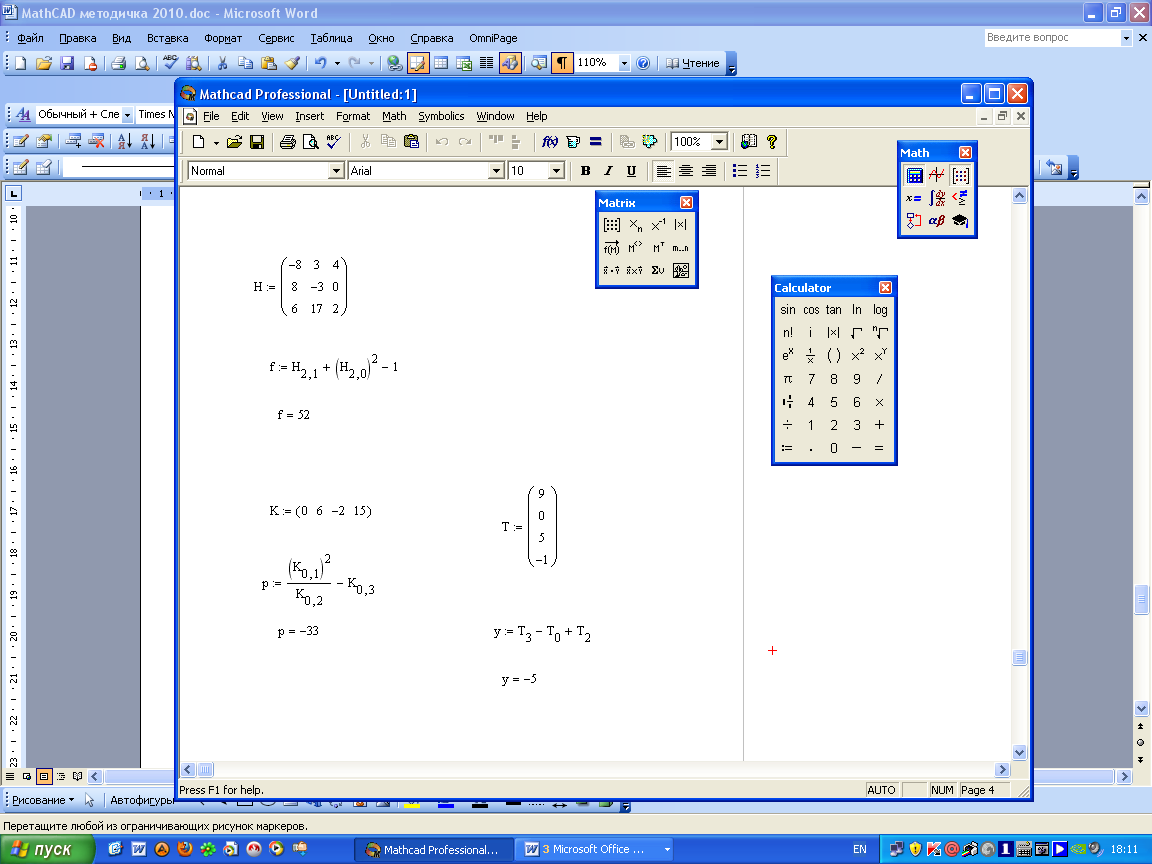
Рассмотрите следующие примеры:

Задания для самостоятельной работы:

1. Создать матрицу 5х5, вручную заполнить числами от -5 до +5. Вычислить сумму всех элементов матрицы.

2. Создать матрицы S и Y, заполнить числами:

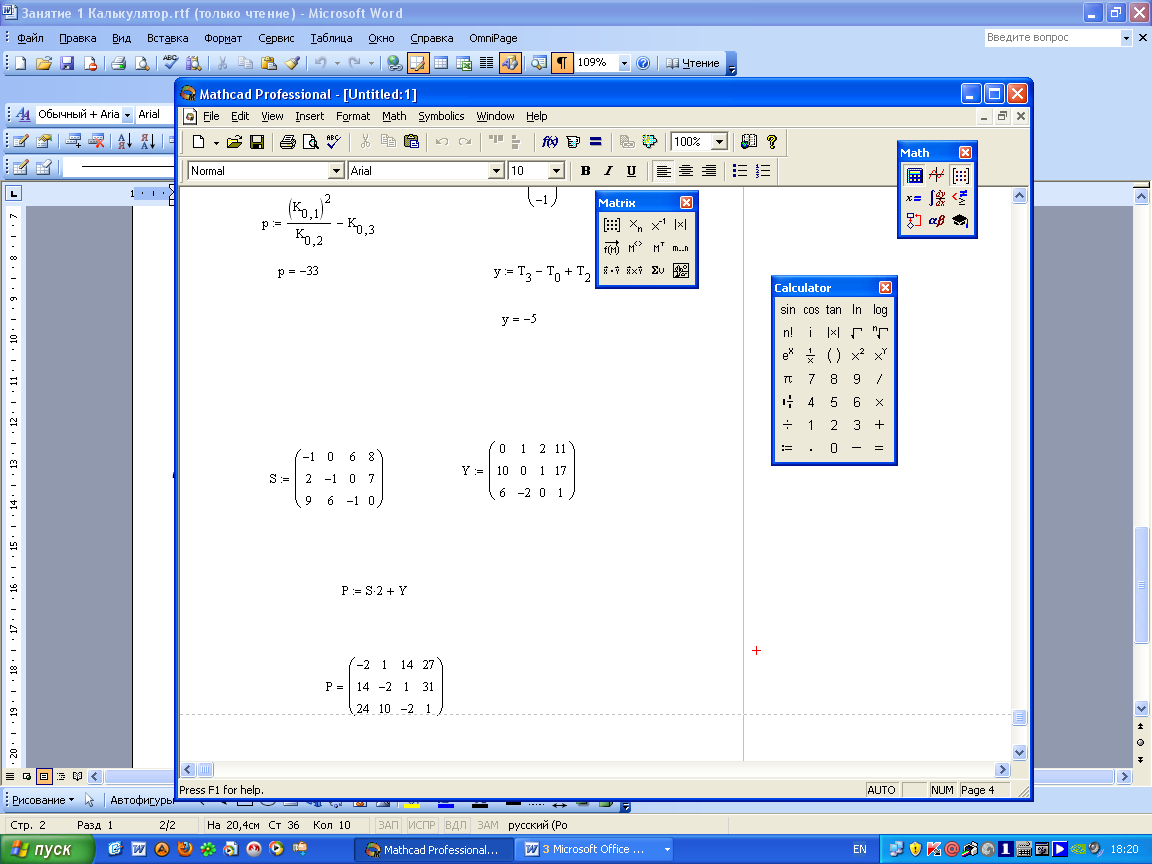
Вычислить следующие формулы и вывести результаты вычислений:

1.
2.
3.

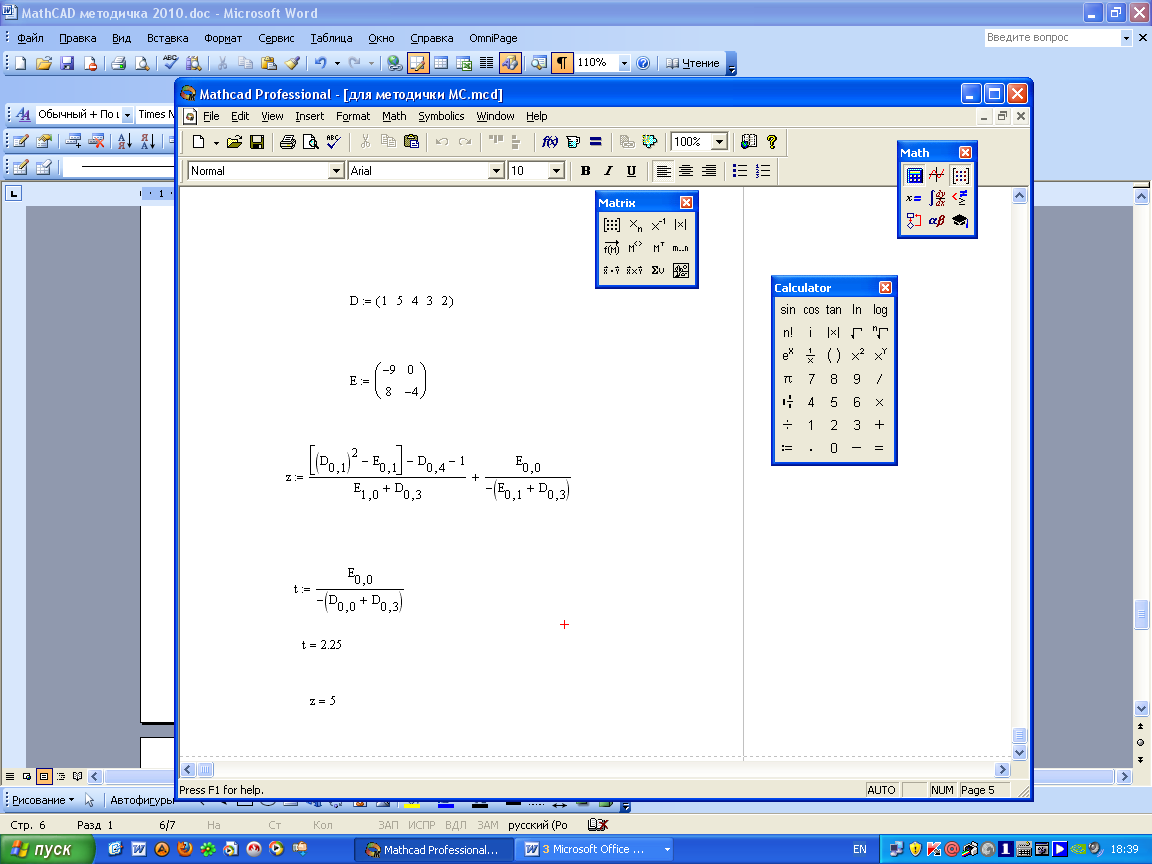
3. Создать матрицы D и S. Вычислить и вывести значение переменной z.