1. Обыкновенные диф. Ур. Общий интеграл, об. Решение, частный интеграл, частное решение. Задача Коши

Уравнение, содержащее независимую переменную, а также неизвестную функцию этой переменной и её производные или дифференциалы, называется обыкновенным дифференциальным уравнением: F(x, y, y, …, у^(п) ) = 0. (1)

Общим решением дифференциального уравнения п-го порядка (1) называют функцию (2)зависящую от аргумента х и п произвольных постоянных С₁,…С_п, и такую, что она при подстановке в уравнение (1) превращает его в тождество.

Общее решение задаётся в неявной форме ,(3) его называют общим интегралом уравнения (1).

Общее решение (общий интеграл), в котором вместо произвольных С₁,…С_п подставлены конкретные числа, называется частным решением (частным интегралом).

Для нахождения значений постоянных С₁,…С_п необходимо задать п начальных условий.

Совместное задание дифференциального уравнения и соответствующего количества начальных данных называется задачей Коши:

(4)

2. Диф. Урав. С разделенными и разделяющимися переменными

Дифференциальное уравнение первого порядка вида N(x)dx+M(y)dy=0 (5) называется дифференциальным уравнением с разделенными переменными.

Общий интеграл такого уравнения находится по формуле:

(6) Дифференциальное уравнение первого порядка вида

P(x)R(y)dx+Q(x)S(y)dy=0 (7) называется дифференциальным уравнением с разделяющимися переменными. Его можно привести к уравнению с разделенными переменными вида (6) путем деления обеих частей на Q(x)R(y):

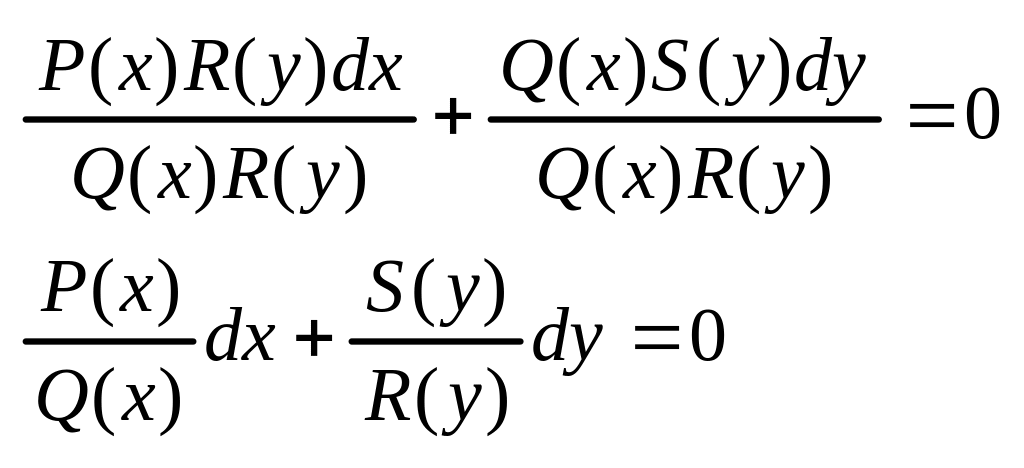Т.е. получим уравнение с разделенными переменными, которое решается интегрированием.

3. Однородные диф. Урав. 1 порядка

Функция называется однородной функцией n-го измерения относительно переменных х и у, если при любом справедливо тождество Дифференциальное уравнение первого порядка (1)

называется однородным относительно х и у, если функция есть однородная функция нулевого измерения относительно х и у , т.е. По условию: . Полагая здесь , получим: , и уравнение (1) запишем так: (1’) Заметим, что перед делением на х следует проверить наличие частного решения . Сделаем подстановку ; ; . ; Подставляя сюда после интегрирования , получим общий интеграл уравнения (1).

4. Линейные диф. Урав. 1 порядка. Метод Бернулли

Урав. вида (1) где и - непрерывные функции на отрезке [a;b] наз. линейным диф. уравн. 1 порядка. Решение уравнения (1) будем искать решение в виде произведения двух функций (2) Тогда Тогда уравнение (1) можно записать в виде: , или (3) Выберем так, чтобы выполнялось равенство: (кроме ) (4) Тогда Окончательно получим общее решение в виде

5. Урав. Бернулли

Уравнения вида (1)где и – непрерывные функции на отрезке [a;b], , называется уравнениями Бернулли. Если к=0 – линейное урав., к=1 – ур-е с разделяющимися переменными, к≠0 к≠1 – приведет это урав. К линейному.Поделим обе части уравнения (1) на , получим (3) замену (4)-линейное д.у. Найдем его общее решение, сделаем в нем обратную замену и получим общее решение уравнения (1).