Тюрникова Г.В. Курс высшей математики для начинающих. Гл.5/14. Неопределенный интеграл.
Интегральное исчисление изучает неопределенные и определенные интегралы, их свойства и вычисление.
(Математическая энциклопедия, т.2.стр.563).
Глава 5. Неопределенный интеграл.
Раздел 5.1. Первообразная функции и неопределенный интеграл.
5.1.1. Основные понятия.
Одной из основных задач дифференциального исчисления является отыскание производной /дифференциала заданной функции.
Различные вопросы математики, естествознания, техники приводят к решению обратной задачи: восстановлению функции по известной ее производной (или известному дифференциалу).
Определение 1. Функция F(х) называется первообразной для функции f(х) на некотором промежутке, если в каждой точке этого промежутка
.
Или, что то же
.
Пример:
1.
;
2
.
.
Определение 2. Семейство первообразных F(x)+C для f(x) на некотором промежутке называется неопределенным интегралом.
Основная задача интегрального исчисления: по данной функции f(х) отыскать все F(x).
Этот факт записывают:
*),
где
Процесс отыскания F(x) и F(x)+C называется интегрированием функции f(x), или, иногда, говорят “взять от f(х) интеграл”.
Заметим, что правильность интегрирования всегда можно проверить дифференцированием результата.
Для одной и той же функции f(х) первообразные могут внешне отличаться друг от друга.
Пример:
;
и
.
Легко убедиться, что производные от левых частей каждого равенства совпадают.
Кстати, потому интегрирование и неопределенное, что при этом не важно, какая из первообразных найдена.
5.1.2. Таблица неопределенных интегралов основных элементарных функций.
Эта таблица*) получается из определения неопределенного интеграла и таблицы дифференциалов основных элементарных функций.
,
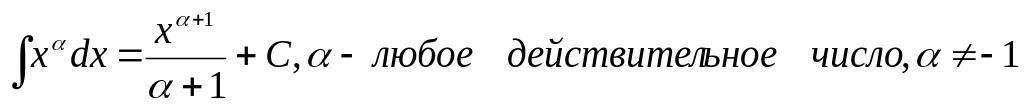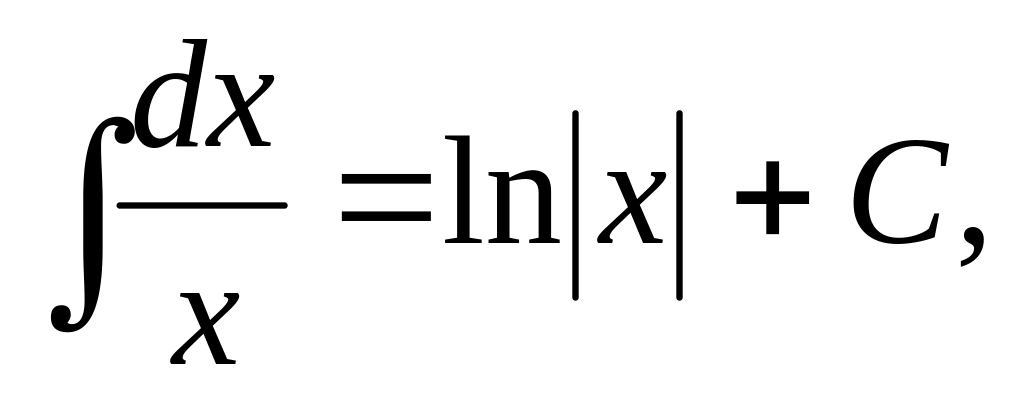
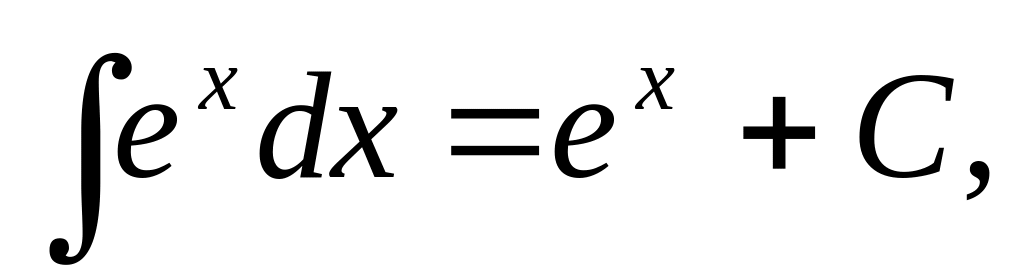
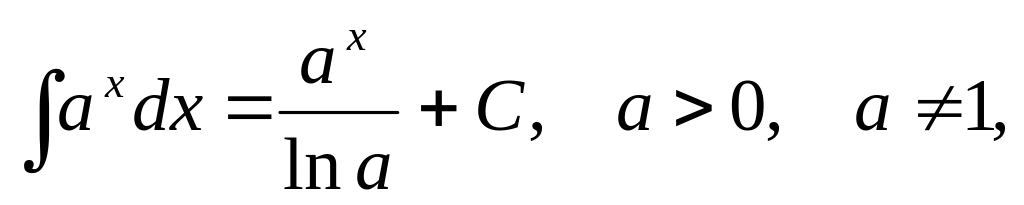
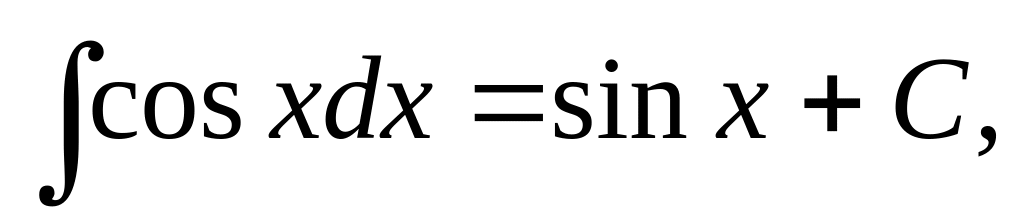
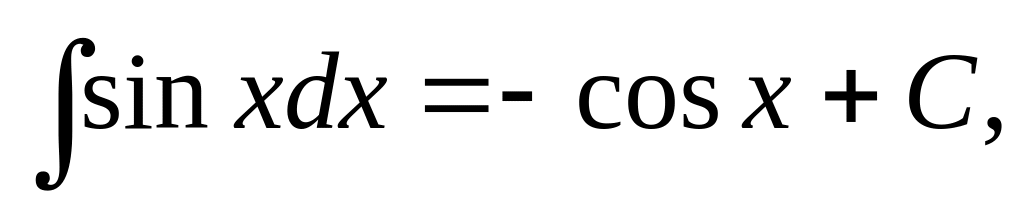
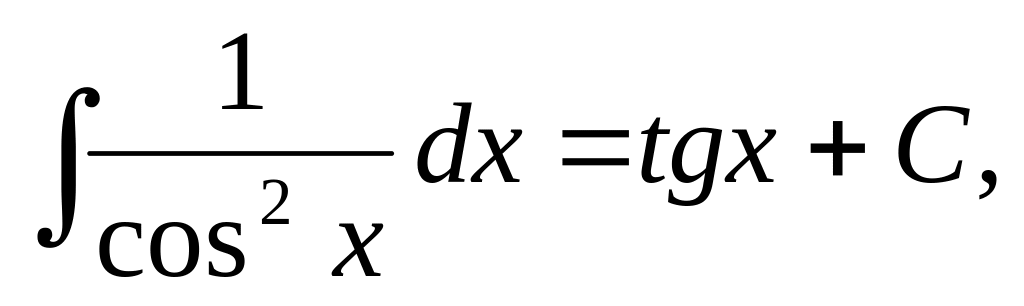
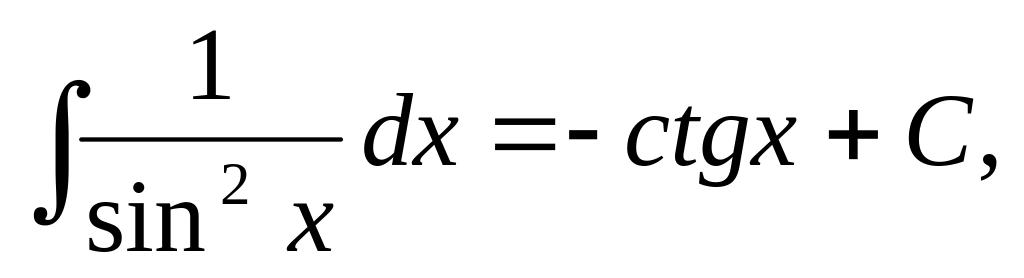
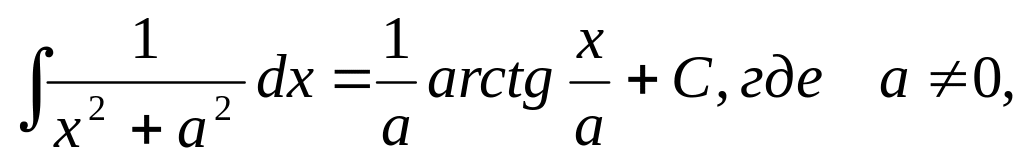
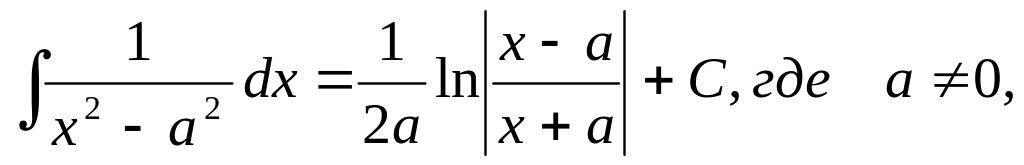
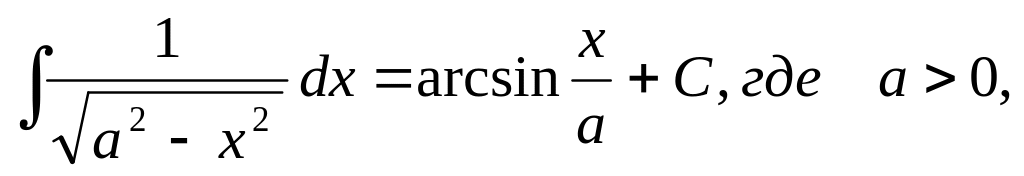
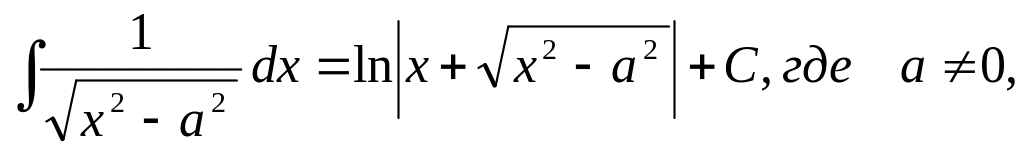
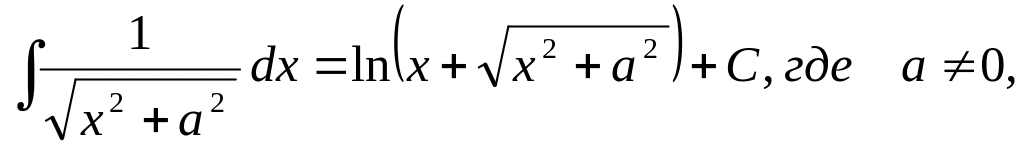
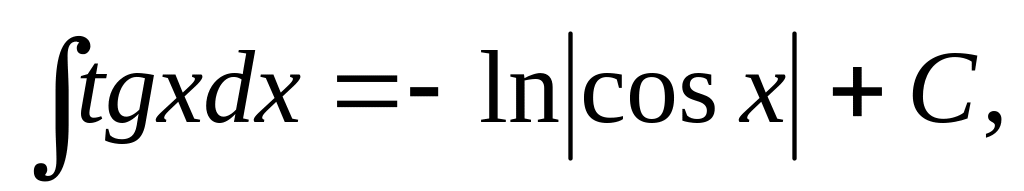
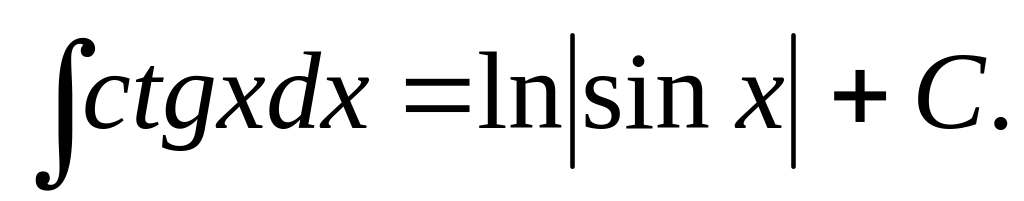
И ответим на вопрос: у всякой ли функции, существует первообразная, и если существует, то одна или их много?
Теорема. Для всякой непрерывной на данном промежутке функции существует первообразная.
В дальнейшем изложении, не обговаривая этого особо, функции, для которых ищутся первообразные, будем считать непрерывными на рассматриваемых промежутках, а конкретные элементарные функции будем рассматривать только на промежутках их непрерывности.
В связи с этим возникает вопрос о так называемых неберущихся (не интегрируемы в элементарных функциях; не интегрируемы в конечном виде) интегралах. Это (примеры):
Следует различать существование неопределенного интеграла и возможность его выражения через элементарные функции. Указанные интегралы существуют, но средств – основных элементарных функций – оказывается недостаточно для того, чтобы составить из них конечные выражения для этих интегралов.
5.1.3.Свойства неопределенного интеграла.
1.
2.
3.
4.
5.
6.
7.Инвариантность формул интегрирования:
,
где
- любая дифференцируемая функция от х.
Заметим, что при практическом интегрировании без этих свойств обойтись невозможно.
Практикум по разделу 5.1.
Задание 1. Найти:
а)
;
б)
;
в)
;
г)
;
д)
.
Задание
2. Найти функцию
так, что:
а)
;
б)
;
в)
;
г)
;
д)
.
Задание 3. Найти неопределенные интегралы:
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
;
з)
;
и)
;
к)
;
л)
;
м)
;
н)
;
о)
.