Санкт-Петербургский Государственный

Электротехнический Университет

ФКТИ

Кафедра МОЭВМ

Дисциплина «Компьютерная графика»

Пояснительная записка

к курсовой работе по теме

" Визуализация воды "

Руководитель: Герасимова Т.В.

Санкт-Петербург

2008 г.

Постановка и анализ задачи

Моделирование водных поверхностей является сложной, но интересной задачей. Здесь можно выделить такие подзадачи, как моделирование небольших водоемов (с видимыми границами), для которых характерны небольшие изменения поверхности, то есть небольшие колебания, а также интерференция колебаний от нескольких всплесков и отраженных колебаний от границ; большие водные поверхности: здесь рассматривают небольшие поверхностные колебания (как правило, в этом случае можно обойтись изменениями лишь текстуры или нескольких текстур поверхности (Bump Mapping и др., см. далее) не деформируя непосредственно саму поверхность), небольшие колебания: в этом случае поверхность разбивается на треугольники, но достаточно большого размера и над поверхностью производят небольшие колебания, которые соответствуют, например, небольшим волнам, большие колебания: этот большие волны, брызги и др., здесь происходят значительные деформации водных поверхностей, которые достаточно сложно физически описываются, поэтому большие волны практически никогда не визуализируются. Брызги можно визуализировать, например, используя массив частиц (маленьких плоскостей, ориентированных по нормали на наблюдателя), для которых устанавливаются начальные скорости, а дальнейший их полет происходит по гравитационному закону.

Моделирование небольших колебаний и небольших волн в простейшем случае можно реализовать с помощью композиций синусных (или косинусных) функций, с установленными некоторыми законами для распространения волны, позволяющие моделировать отражения волн от границ, интерференцию волн и другое. Синусные функции могут передавать характеристики волны, и результаты могут быть достаточными в ряде приложений. Но данный метод является в достаточной мере эвристическим, и мы его рассматривать не будем, так как применение его в достаточной мере ограничено.

Моделирование небольшие водных поверхностей.

 

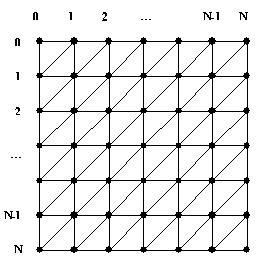
Предположим, что водная поверхность представляет собой квадратную сетку размером NxN. Водная поверхность обладает связностью (в физическом смысле), то есть внешнее воздействие на какой-то один узел влечет также изменение, как минимум, в соседних узлах. Физически описать такое взаимодействие можно описать с достаточной степенью точности, если предположить, что соседние узла связаны между собой линейно-упругой пружиной.

Для каждого узла вводятся следующие характеристики:

m_i- масса узла;

- декартовы координаты узла;

- скорость узла;

- ускорение узла;

- сумма всех сил, действующих на узел;

Выводить на экран такую поверхность можно следующим образом: для каждых четырех узлов: p_ijp_i+1jp_i+1j+1p_ij+1 на экран выводятся 2 треугольника:p_ijp_i+1jp_ij+1 иp_ij+1p_i+1jp_i+1j+1.

Выражение для силы пружины S_k, действующей на узелp_i, следует из закона Гука:

(1)

где ,- длина покоя и текущая длина пружины соответственно;- единичный вектор в направлении пружины.

Или, если расписать:

(1)'

Уравнения движения всей такой системы легко выводятся из общего курса физики:

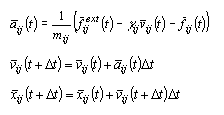
- масса узла;- сумма сил пружин, прикрепленных к узлу;- сумма внешних сил, приложенных к узлу;- коэффициент демпфирования, характеризующий сопротивление среды, в которой движется узел.

Неплохие результаты дают следующие характеристики системы:

Шаг сетки, H	Масса узла, mij	Коэффициент упругости, ск	Демпфирование,	Шаг интегрирования,
1.0	4.0	7.0	0.05	0.4

Управлять возмущением такой системы достаточно просто: необходимо лишь изменять вектор внешних сил на некоторые узлы решетки (то есть непосредственно осуществлять внешнее воздействие). Достаточно интересным (может быть, даже более более красивым с точки зрения графики) является подход, когда мы изменяем непосредственно координаты и скорости в некоторых узлах, то есть сразу указываем результат воздействия. Также возможны гибридные подходы этих двух методов.

Задавая различные условия на узлах мы можем моделировать различные водные поверхности с различными граничными и поверхностными условиями. Например, если мы хотим моделировать бассейн или некоторую другую емкость с водой, то необходимо разрешить лишь вертикальные перемещения граничных узлов, то есть положить их горизонтальные перемещения равными нулю. Также, здесь будет хорошо заметна интерференция волн и отражение волн от границы. Если нам необходимо получить небольшой водоем, для которого характерна неизменная береговая линия, то необходимо полностью запретить перемещения граничных узлов.

Если запретить горизонтальные перемещения на все узлы, то это подчеркнет эффект прохождения волн друг сквозь друга. Также если запретить перемещения некоторых внутренних узлов, то можно смоделировать, например, островок, от которого волны будут также еще и отражаться. В данном случае узлы должны повторять контур островка.

Чтобы задать точечное возмущение можно воспользоваться следующими способами: изменить скорость в данном узле и в некоторой его окрестности, или сделать тоже самое с координатами. Характер возмущения описывается с помощью гауссовского распределения с некоторым радиусом. Также, чтобы данный процесс не замедлял основной цикл программы, данные значения просчитываются заранее, заносятся в массив, а затем во время работы программы прибавляются к текущим координатам или скоростям узлов.