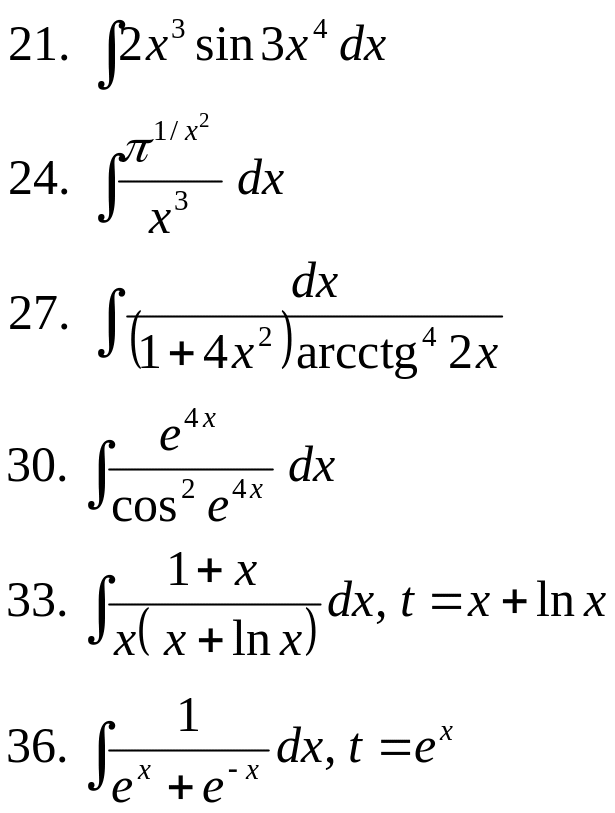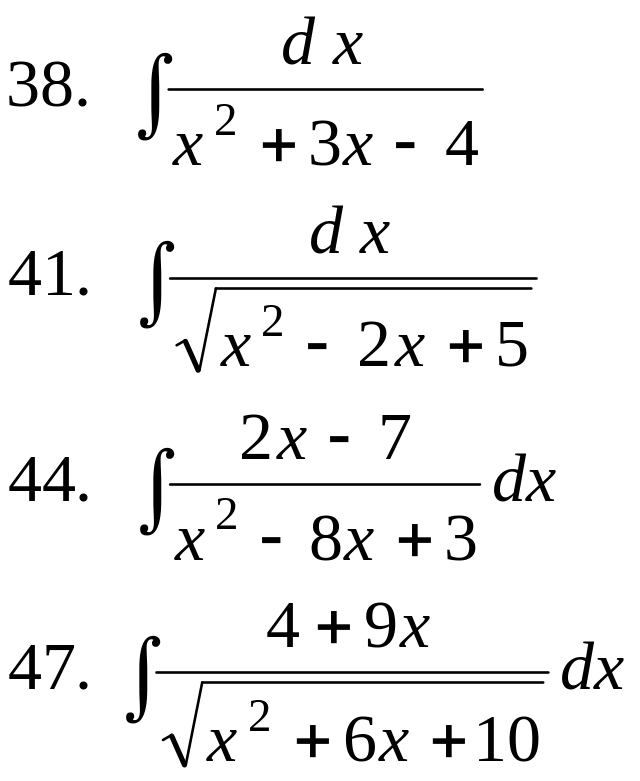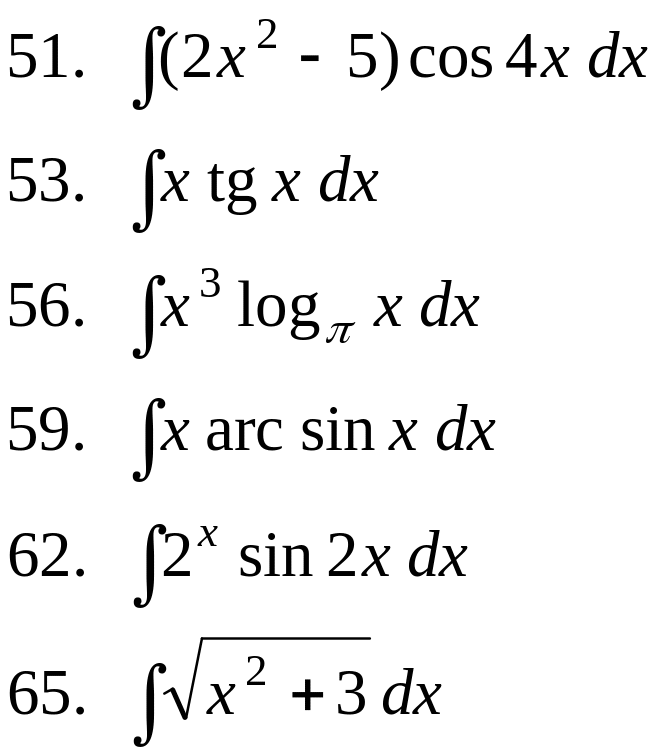Неопределенный интеграл

Первообразная и неопределенный интеграл

Определение: Первообразной непрерывной функции f(x) на интервале (a; b) называется функция F(x), производная которой равна f(x) во всех точках данного интервала: F′(x) = f(x)

Теорема: Если есть две первообразные функции f(x), то они отличаются друг от друга только на постоянную величину.

Определение: Совокупность всех первообразных функции f(x) называется неопределенным интегралом.

где – знак интеграла, f(x) – подынтегральная функция, dx – знак дифференциала, f(x) d x – подынтегральное выражение.

Теорема: Непрерывная на отрезке [a; b] функция интегрируема на интервале (a; b) (т.е. существует первообразная или неопределенный интеграл).

Свойства неопределенного интеграла:

Способы вычисления интегралов

I. Табличное интегрирование

Метод интегрирования, при котором данный интеграл путём тождественных преобразований подынтегральной функции и применения свойств интеграла приводится к одному или нескольким табличным интегралам называется непосредственным интегрированием.

Таблица интегралов (u=u(x)):

˜Пример I.1. Вычислить интеграл

Решение:

˜Пример I.1а. Вычислить интеграл

II. Линейное преобразование выражения под знаком дифференциала

Если известен интеграл , то следующие интегралы могут быть вычислены с помощью линейного преобразования выражения под знаком дифференциала:

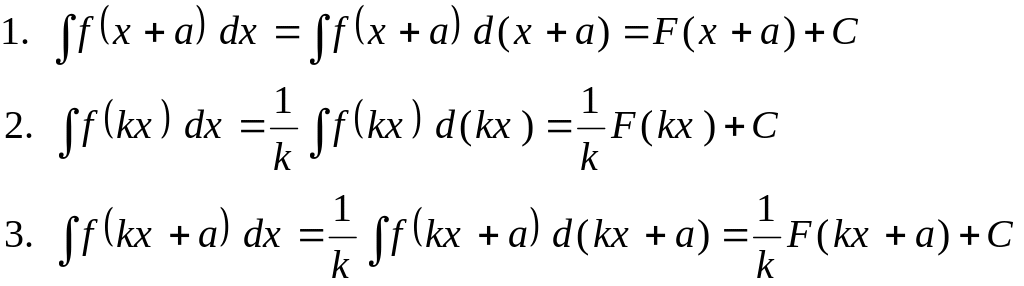
˜Пример II.1. Вычислить интеграл

Решение:

Вычислить интегралы:

III. Подведение (внесение) под знак дифференциала.

Один из множителей подынтегральной функции можно подвести под знак дифференциала. Для этого необходимо вычислить первообразную этого множителя и записать ее под знаком дифференциала. В дальнейшем все дополнительные вычисления и рассуждения будем записывать между двумя вертикальными чертами.

!Совет. Если после внесения одного из множителей под знак дифференциала возникли затруднения в дальнейших действиях, смело заменяйте полученное выражение под знаком дифференциала на новую переменную.

˜Пример III.1. Вычислить интеграл

Решение:

IV. Замена переменной под знаком интеграла (подстановка)

В неопределенном интеграле переменную интегрирования можно заменить на непрерывную и дифференцируемую функцию от другой переменной:

˜Пример IV.1. Вычислить интеграл

Решение:

Вычислить интегралы:

V. Интегрирование выражений, содержащих квадратный трехчлен в знаменателе.

При интегрировании выражений, содержащих квадратный трехчлен в знаменателе:

необходимо использовать подстановку: .

˜Пример V.1. Вычислить интеграл

Решение:

Пример V.1а. Вычислить интеграл

Решение:

Вычислить интегралы:

VI. Интегрирование по частям.

Формула интегрирования по частям

Случаи применения формулы интегрирования по частям:

Замечания:

1. Через Tr(x) обозначена тригонометрическая функция, P_n(x) означает многочлен степени n, а в квадратных скобках перечислены функции, к которым применима данная формула.

2. Во втором пункте вместо многочлена можно подставлять и степенную функцию.

˜Пример VI.1. Вычислить интеграл

Решение:

˜ Пример VI.2. Вычислить интеграл

Решение:

˜ Пример VI.3. Вычислить интеграл

Решение:

Вычислить интегралы:

VII. Интегрирование рациональных дробей.

Определение. Рациональной дробью называется отношение двух многочленов: R(x) = , где P_m(x) – многочлен степени m, а Q_n(x) – многочлен степени n.

Определение. Рациональная дробь называется правильной, если степень многочлена в числителе меньше степени многочлена в знаменателе m < n, и неправильной, если m ≥ n.

Теорема. Неправильную дробь всегда можно представить в виде суммы многочлена (целая часть) и правильной дроби (дробная часть), если разделить числитель на знаменатель.

Например, дробь - неправильная. Разделим числитель на знаменатель:

Здесь целая часть равна (х - 1) , остаток деления равен (2х + 1) и, следовательно,

наша рациональная дробь представляется в следующем виде:

Определение. Правильные рациональные дроби вида

где A, B, C, E, L, K, a, p, q - действительные числа, называются простейшими рациональными дробями.

Теорема. Всякий многочлен с действительными коэффициентами Q_n(x), степень которого выше двух (n > 2), можно разложить на линейные и квадратные множители с действительными коэффициентами, то есть многочлен можно представить в виде:

Здесь k₁+k₂+…+k_s +l_{1 +}l₂ +…+ l_r = n и все квадратные трёхчлены не имеют действительных корней, то есть их дискриминанты меньше нуля.

Теорема. Всякую правильную рациональную дробь , знаменатель которой разложен на множители :

можно представить единственным образом в виде суммы простейших дробей:

Алгоритм разложения:

1. Привести дробь к правильному виду (в дальнейшем будем рассматривать только правильную дробь).

2. Найти корни знаменателя правильной дроби и разложить его на линейные и квадратные множители.

3. Представить дробь в виде суммы всевозможных различных простейших дробей, в знаменателях которых стоят всевозможные множители знаменателя, а в числителях соответствующей степени многочлены с неопределенными коэффициентами.

! Контроль. Число неопределенных коэффициентов должно равняться степени многочлена в знаменателе исходной дроби.

4. Привести сумму простейших дробей к общему знаменателю. Общим знаменателем является знаменатель исходной дроби.

5. Приравнять числители получившейся и исходной дроби. Вычислить неопределённые коэффициенты. Для этого можно воспользоваться двумя способами: 1) приравнять коэффициенты при соответствующих степенях х в числителях многочленов в правой и левой частях равенства; 2) подставить вместо х конкретные числовые значения (в первую очередь – корни знаменателя). Лучше всего комбинировать эти два способа.

Общее правило интегрирования рациональных дробей:

1. Если под знаком интеграла стоит неправильная дробь, то путём деления числителя на знаменатель, её нужно представить в виде суммы многочлена и правильной дроби.

2. Разложив знаменатель правильной рациональной дроби на множители, представить её в виде суммы простейших рациональных дробей.

3. Вычислить интеграл от многочлена и каждой из простейших рациональных дробей.

˜ Пример VII.1. Вычислить интеграл

Решение:

Приравниваем числители:

.

Находим неопределённые коэффициенты: подставляя х = -1, получим 2 = D; сравнивая коэффициенты при х³, имеем А = 0. Выписываем коэффициенты при х²: 1 = 3A + B, следовательно, В = 1. При х = 0 имеем: 1 = A + B + C + D и С = 2.

Подставляем полученные коэффициенты в разложение:

;

Находим интегралы от простейших дробей

˜ Пример VII.2. Вычислить интеграл

Решение: Так как дробь является неправильной, разделим числитель на знаменатель:

Подынтегральная функция при этом представляется в следующем виде:

Разложим правильную дробь на сумму простейших:

Вычислить интегралы: