
- •Математическое программирование.
- •Введение
- •1. Целочисленное программирование
- •Метод Гомори
- •Метод ветвей и границ
- •1.3 Задачи для самостоятельной работы
- •2. Теория игр
- •2.1. Основные положения теории игр
- •2.2. Решение матричной игры в чистых стратегиях
- •2.3. Решение матичной игры в смешанных стратегиях
- •2.4. Игра 2 2
- •2.5. Сведение матричной игры к задаче линейного программирования
- •2.6. Игры с природой
- •2.7. Задачи для самостоятельной работы
- •3. Линейный межотраслевой баланс
- •3.2. Задачи для самостоятельной работы
- •4. Нелинейное программирование
- •4.1 Постановка задача нелинейного программирования
- •4.2 Решение задач нелинейного программирования с ограничениями-равенствами
- •4.3. Решение задач нелинейного программирования с ограничениями-неравенствами
- •4.4. Задачи для самостоятельной работы
- •5. Динамическое программирование
- •Долл., долл.,
- •5.3 Задачи для самостоятельной работы
- •6. Контрольные задания
- •Литература
- •Содержание
- •Математическое программирование
2.6. Игры с природой
В некоторых задачах, приводящихся к игровым, имеется неопределенность, вызванная отсутствуем информации об условиях, в которых осуществляется действие (погода, покупательный спрос и т.д.). Эти условия зависят не от сознательных действий другого игрока, а от объективной действительности. Такие игры называются играми с природой. Человек в играх с природой старается действовать осмотрительно, второй игрок (природа, покупательный спрос) действует случайно.
Условия игры задаются матрицей
.
Имеется ряд критериев принятия решений, которые используются при выборе оптимальной стратегии.
1. Критерия Бейеса-Лапласа.
Пусть игрок А выбирает стратегии
А1, А2, …, Аm,
а природа – состояния В1,
В2,…,Вn.
Наиболее простой является ситуация,
когда известна вероятность
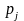 каждого состояния природы Вj.
При этом, если учтены все возможные
состояния,
каждого состояния природы Вj.
При этом, если учтены все возможные
состояния,
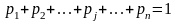 .
.
Если игрок А выбирает чистую стратегию
Аi, то математическое
ожидание выигрыша составит
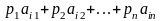 .
Наиболее выгодно будет та стратегия,
при которой достигается
.
Наиболее выгодно будет та стратегия,
при которой достигается
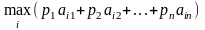 .
.
Тогда критерием принятия решений является максимум математического ожидания, т.е.
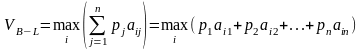 .
.
2. Критерия Лапласа.
Данный критерий опирается на «принцип
недостаточного основания» Лапласа,
согласно которому все состояния природы
Вj, полагаются
равновероятными
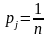 .
Тогда оптимальной является стратегия
.
Тогда оптимальной является стратегия
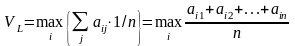 ,
,
т.е. стратегия, для которой среднее арифметическое элементов соответствующей строки максимальное.
3. Критерий Вальда. (минимаксный или максиминный)
Данный критерий опирается на принцип наибольшей осторожности и основывается на выборе наилучшей из наихудших стратегий Аi. Выбранные варианты полностью исключают риск, т.е. принимающий решение не может столкнуться с худшим результатом, чем тот, на который он ориентируется. Данный критерий не требует знания вероятностей состояний Вj.
Если в исходной матрице результат представляет потери лица, принимающего решение, то при выборе оптимальной стратегии используется минимаксный критерий:
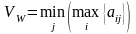 .
.
Таким образом, для определения оптимальной стратегии Аi необходимо в каждой строке матрицы найти сначала наибольший элемент, а затем среди них выбрать наименьший.
Если в исходной матрице результат представляет выигрыш (полезность) лица, принимающего решение, то при выборе оптимальной стратегии используется максиминный критерий:
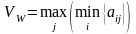 .
.
4. Критерия минимального риска Сэвиджа;
Суть критерия состоит в выборе такой стратегии, чтобы не допустить высоких потерь, к которым она может привести. Находится матрица рисков, элементы которой показывают, какой убыток понесет человек (фирма), если для каждого состояния природы он не выберет наилучшей стратегии.
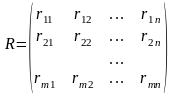 .
.
Элементы матрицы рисков находятся по
формуле
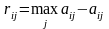 ,
где
,
где
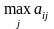 - максимальный элемент в столбце исходной
матрицы.
- максимальный элемент в столбце исходной
матрицы.
Оптимальная стратегия определяется
выражением
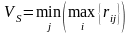 .
.
5. Критерия Гурвица.
Данный критерий основан на следующих
двух предположениях: природа может
находится в самом невыгодном состоянии
с вероятностью
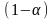 и в самом выгодном состоянии с вероятностью
,
где
- коэффициент доверия.
и в самом выгодном состоянии с вероятностью
,
где
- коэффициент доверия.
Критерий
Гурвица устанавливает баланс между
случаями крайнего пессимизма и крайнего
оптимизма путем взвешивания обоих
способов поведения соответствующими
весами
и
,
где
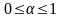 .
.
Если в исходной задаче матрица представляет выигрыш, прибыль, полезность, доход и т.п., то критерий Гурвица записывается
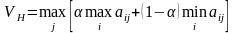 .
.
Если матрица представляет затраты
(потери), то критерий Гурвица записывается
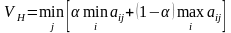 .
.
Если
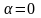 ,
получим критерий Вальда, а если
,
получим критерий Вальда, а если
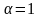 ,
то приходим к решающему правилу вида
,
то приходим к решающему правилу вида
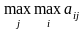 .
.
Пример
9. Определить, какой тип R1,
R2, R3,
R4 самолета
необходимо построить, чтобы удовлетворить
потребность авиаперевозчиков.
Экономическая эффективность строительства
самолетов зависит от влияния случайных
факторов, образующих множество состояний
природы
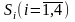 .
Результаты расчета экономической
эффективности приведены в таблице.
Проанализировать ситуацию и выбрать
оптимальную стратегию:
.
Результаты расчета экономической
эффективности приведены в таблице.
Проанализировать ситуацию и выбрать
оптимальную стратегию:
на основании критерия Бейеса-Лапласа, определяя А в
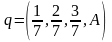 ,
где qj
– вероятности j-го
состояния «природы»;
,
где qj
– вероятности j-го
состояния «природы»;на основании критерия Лапласа в предположении, что все состояния природы равновероятны;
используя максимальный критерий Вальда;
на базе критерия минимального риска Сэвиджа;
на основании критерия Гурвица с заданным значением =0,6.
-
Тип самолета
Состояние природы
S1
S2
S3
S4
R1
5
2
8
4
R2
2
3
4
12
R3
8
5
3
10
R4
1
4
2
8
Решение. 1) Определим константу
А из требования выполнения равенства
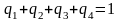 ,
откуда А=1/7.
,
откуда А=1/7.
Определим математическое ожидание выигрыша при выборе им стратегии Аi:
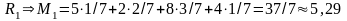 ;
;
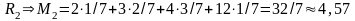 ;
;
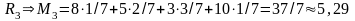 ;
;
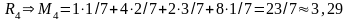 .
.
По критерию Бейеса-Лапласа критерием принятия решений является максимум математического ожидания, т.е.
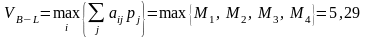 .
.
В соответствии с этим критерием наиболее предпочтительными являются стратегии R1 и R3.
2) Если предположить, что все состояния
природы равновероятны, то
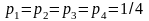 ,
то для принятия решения следует найти
математическое ожидание выигрыша:
,
то для принятия решения следует найти
математическое ожидание выигрыша:
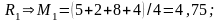
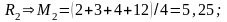
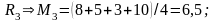
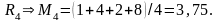
По критерию Лапласа оптимальной является стратегия
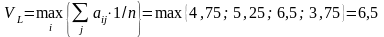 .
.
Тогда оптимальной является стратегия R3.
3) Согласно критерию Вальда
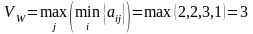 .
.
Следовательно, максимальная стратегия - R3.
4) Для выбора оптимальной стратегии по критерию Сэвиджа вначале построим матрицу рисков, элементы которой вычисляются по формуле .
Имеем матрицу рисков
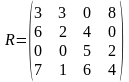 .
.
Тогда согласно критерию Сэвиджа
определяем
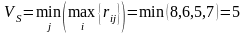 .
В соответствии с этим критерием также
предпочтительна стратегия R3.
.
В соответствии с этим критерием также
предпочтительна стратегия R3.
Воспользуемся критерием Гурвица при =0,6. Определим значение
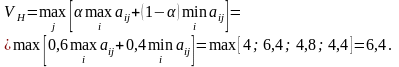
Таким образом, согласно критерию Гурвица оптимальной является стратегия R2.
Вывод: анализ результатов проведенных на основе различных критериев показывает, что наиболее приемлемой является стратегия R3.
