
- •Математическое программирование.
- •Введение
- •1. Целочисленное программирование
- •Метод Гомори
- •Метод ветвей и границ
- •1.3 Задачи для самостоятельной работы
- •2. Теория игр
- •2.1. Основные положения теории игр
- •2.2. Решение матричной игры в чистых стратегиях
- •2.3. Решение матичной игры в смешанных стратегиях
- •2.4. Игра 2 2
- •2.5. Сведение матричной игры к задаче линейного программирования
- •2.6. Игры с природой
- •2.7. Задачи для самостоятельной работы
- •3. Линейный межотраслевой баланс
- •3.2. Задачи для самостоятельной работы
- •4. Нелинейное программирование
- •4.1 Постановка задача нелинейного программирования
- •4.2 Решение задач нелинейного программирования с ограничениями-равенствами
- •4.3. Решение задач нелинейного программирования с ограничениями-неравенствами
- •4.4. Задачи для самостоятельной работы
- •5. Динамическое программирование
- •Долл., долл.,
- •5.3 Задачи для самостоятельной работы
- •6. Контрольные задания
- •Литература
- •Содержание
- •Математическое программирование
Метод ветвей и границ
Метод ветвей и границ – один из комбинированных методов. Его суть заключается в упорядоченном переборе вариантов и рассмотрении лишь тех из них, которые оказываются по определенным признакам перспективными, и отбрасывании бесперспективных вариантов.
Метод ветвей и границ состоит в следующем: множество допустимых решений (планов) некоторым способом разбивается на подмножества, каждое из которых этим же способом снова разбивается на подмножества. Процесс продолжается до тех пор, пока не получено оптимальное целочисленное решение исходной задачи.
Пусть требуется решить задачу
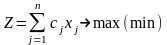 (1.6)
(1.6)
при ограничениях
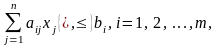 (1.7)
(1.7)
 (1.8)
(1.8)
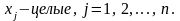 (1.9)
(1.9)
Как и при решении сформулированной задачи методом Гомори, процесс начинается с решения непрерывной задачи линейного программирования без учета целочисленности. Если полученный оптимальный результат не содержит дробных чисел, найдено искомое решение.
Если полученный оптимальный результат
Хопт не удовлетворяет условию
(1.9), то значение целевой функции дает
верхнюю оценку искомого решения на
множестве G, заданном
условиями (1.7), (1.8). При этом если имеется
некоторая нецелочисленная переменная,
то в целочисленном плане ее следует
либо уменьшить до значения
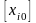 ,
либо увеличить до
,
либо увеличить до
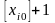 ,
т.е. из области допустимых решений
исключается область
,
т.е. из области допустимых решений
исключается область
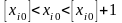 .
Где
- целая часть числа. Тем самым из исходной
задачи формируется две задачи: 2 и 3,
отличающиеся друг от друга тем, что в
задаче 2 кроме ограничений (1.7), (1.8)
исходной задачи добавлено ограничение
.
Где
- целая часть числа. Тем самым из исходной
задачи формируется две задачи: 2 и 3,
отличающиеся друг от друга тем, что в
задаче 2 кроме ограничений (1.7), (1.8)
исходной задачи добавлено ограничение
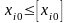 ,
а в задаче 3 кроме ограничений (1.7), (1.8)
исходной задачи добавлено ограничение
,
а в задаче 3 кроме ограничений (1.7), (1.8)
исходной задачи добавлено ограничение
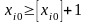 .
.
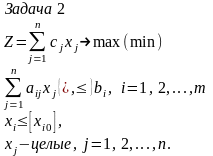
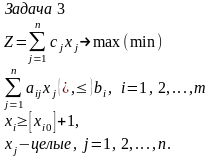
Находим решение задач 2 и 3 методами линейного программирования. Возможен один из следующих случаев:
Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции на нем дают решение исходной задачи.
Одна из задач неразрешима, а другая имеет оптимальный план, среди компонент которого есть дробные числа. Тогда рассматриваем вторую задачу и в ее оптимальном плане выбираем одну из компонент, значение которой равно дробному числу, и строим задачи аналогичные задачам 2 и 3.
Обе задачи разрешимы. Одна из задач имеет оптимальный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значения целевой функции на этих планах и сравниваем их между собой. Если на целочисленном оптимальном плане значение целевой функции больше или равно ее значению ее значению на плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи, и он вместе со значением целевой функции на нем дает искомое решение.
Если же значение целевой функции больше на плане, среди компонент которого есть дробные числа, то следует взять одно из таких чисел и для задачи, план которой рассматривается, необходимо построить две задачи, аналогичные 2 и 3.
Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда вычисляем значение целевой функции на данных оптимальных планах и рассматриваем ту из задач, для которой значение целевой функции является наибольшим. В оптимальном плане этой задачи выбираем одну из компонент, значение которой является дробным числом, и строим две задачи, аналогичные 2 и 3.
Итерационный процесс продолжается до тех пор, пока не будет найдена вершина, соответствующая целочисленному плану задачи и такая, что значение функции в этой вершине больше или равно значению функции в других возможных для ветвления вершин.
Пример 2. Методом ветвей и границ найти решение задачи
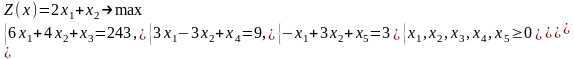
Решение.
Используя симплекс-метод, найдем решение
задачи без учета целочисленности. В
результате получаем оптимальный план
(18/5, 3/5, 0, 0, 24/5). Так как в этом плане
значения трех переменных являются
дробными числами, то этот план не
удовлетворяет условию целочисленности,
и следовательно, не является оптимальным
планом исходной задачи. Возьмем
какую-нибудь переменную, значение
которой является дробным числом, например
х1.
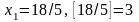 .
Тогда эта переменная в оптимальном
плане исходной задачи будет принимать
значение, либо меньше или равно 3, либо
большее или равное 4.
.
Тогда эта переменная в оптимальном
плане исходной задачи будет принимать
значение, либо меньше или равно 3, либо
большее или равное 4.
Рассмотрим две задачи линейного программирования:
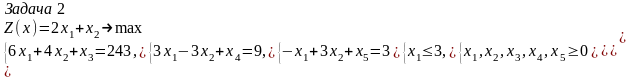

Задача 2 имеет оптимальный план (3, 3/2, 0, 9/2, 3/2). Задача 3 неразрешима.
Исследуем задачу 2. Так как среди компонент оптимального плана этой задачи есть дробные числа, то для одной из переменных, например х2, вводим дополнительные ограничения:
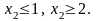
Рассмотрим теперь следующие две задачи:
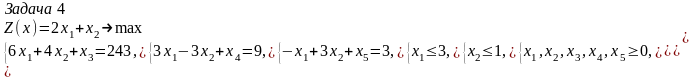
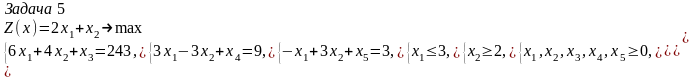
Задача 5 неразрешима, а задача 4 имеет оптимальный план (3, 1, 2, 3, 3), на котором значение целевой функции Z(x)=7.
Таким образом, исходная задача целочисленного программирования имеет оптимальный план (3, 1, 2, 3, 3). При этом плане целевая функция задачи принимает максимальное значение Z(x)=7.
