Прилади для виміру абсолютного тиску р  манометри абсолютного тиску. Манометри абсолютного тиску звичайно застосовують для виміру малих абсолютних тисків.

Абсолютний тиск можна вимірювати також за допомогою барометра й манометра, якщо вимірюваний тиск більше атмосферного ( ), а також барометра й вакуумметра, якщо вимірюваний тиск менше атмосферного ( ).

4. Прилади для виміру різниці тисків – диференціальні манометри.

5. Прилади для виміру малого надлишкового тиску й вакууму – мікроманометри.

За принципом дії розрізняють прилади:

• рідинні;

• пружинні;

• поршневі;

• електричні;

• комбіновані й ін.

До рідинних відносяться прилади, що засновані на використанні гідростатичного закону розподілу тиску. Принцип дії полягає в тім, що вимірюваний тиск урівноважується тиском, створюваним вагою стовпа робочої рідини. Висота стовпа робочої рідини служить мірою тиску.

Дія пружинних манометрів заснована на застосуванні закону Гука. Сила тиску деформує пружний елемент приладу. Деформація пружного елемента пропорційна тиску й служить його мірою. Пружний елемент приладу – пружина, яка може являти собою мембрани (плоскі, опуклі, гофровані), сильфони (тонкостінні трубки з поперечним гофруванням), трубчасті пружини овального перетину (пружини Бурдона).

У поршневих приладах сила вимірюваного тиску рідини, прикладена до поршня приладу, урівноважується зовнішньою силою, величина якої служить мірою тиску.

Дія електричних приладів заснована на використанні пропорційності між зміною деяких електричних властивостей матеріалів і зміною тиску. Наприклад, омічний опір деяких сплавів пропорційний тиску навколишнього середовища. Ця властивість використовується для виміру високих тисків. При вимірі швидкозмінних тисків використовується властивість провідників змінювати електричний опір при деформації. Електричний дротовий датчик наклеюють на пружний елемент, що деформується під дією вимірюваного тиску.

До комбінованих належать прилади, принцип дії яких носить змішаний характер (наприклад, електромеханічні прилади).

Основними характеристиками приладів, що вимірюють тиск, є:

• клас точності;

• діапазон вимірюваних тисків;

• чутливість;

• лінійність - лінійна залежність між вимірюваною величиною й показанням приладу;

• швидкодія.

Рідинні прилади.

Основними перевагами рідинних приладів є:

• простота пристрою;

• стабільність показань;

• висока точність вимірів.

Основними недоліками рідинних приладів є:

• вузькість діапазону вимірюваних тисків (від 10 до 10⁵ Па);

• крихкість скляних трубок;

• необхідність користуватися для збільшення діапазону вимірюваних тисків ртуттю й іншими рідинами, пари яких отрутні.

Рідина, що використовується в якості робочої, повинна бути малов’язкою і мати малий коефіцієнт теплового розширення. Звичайно як робочі рідини використовують воду ( кг/м³), спирт ( кг/м³), ртуть ( кг/м³), тетраброметан ( кг/м³), бромистий етилен ( кг/м³), бромистий етил ( кг/м³). Наведені значення щільності відповідають температурі Т = 273 К.

З метою зменшення помилки через капілярність у приладах використовують скляні трубки діаметром 10...15 мм для води й 6...9 мм для ртуті.

Ртутний барометр (рис. 1.1). Основна частина барометра - вертикальна товстостінна скляна трубка зі шкалою й із запаяним верхнім кінцем, з якої повністю вилучене повітря. Нижній кінець трубки опущений у чашу із ртуттю, у якій на вільну поверхню робочої рідини діє атмосферний тиск.

Наслідок із закону Паскаля для горизонтального рівня , сполученого з поверхнею ртуті в чаші, дозволяє дорівняти атмосферний тиск і тиск стовпа ртуті в трубці, тобто

р_бар = р_рт = _р  g  h,

де - щільність робочої рідини (ртуті), ;

- прискорення вільного падіння, ;

- висота стовпа ртуті в трубці, м.

Висота h є мірою атмосферного тиску .

Рисунок 1.1 - Принципова Рисунок 1.2 - Барометри водяний (а) і ртутний (б)

схема рідинного

барометра

Рисунок 1.3 - П’єзометр Рисунок 1.4 - Вакуумметр

Погрішністю, що обумовлена тиском насичених пар ртуті у вільному запаяному кінці трубки, можна зневажити, тому що цей тиск на два порядки менше атмосферного тиску ( ).

При конструюванні рідинних приладів важливий раціональний вибір робочої рідини. Так, нормальний атмосферний тиск дорівнює р_бар = 101325 Па. Якщо вибрати за робочу рідину воду, то висота водяного барометра буде більше 10 м (рис. 1.2, а):

h = = = 10,33 м.

Щоб зменшити габарити барометра, за робочу рідину використовують ртуть. Висота ртутного барометра не перевищує 1 м (рис. 1.2, б):

h = = = 0,76 м.

П’єзометр (від греч. piezo - давлю). Застосовується для виміру надлишкового (манометричного) тиску в розглянутій точці. Являє собою вертикальну скляну трубку зі шкалою. Верхній кінець трубки відкритий в атмосферу. Нижній кінець п’єзометра з'єднується з місцем виміру тиску (рис. 1.3). Абсолютний тиск у точці С у відповідності з основним гідростатичним законом визначається вираженням

р_с = р_бар +   g  h_c,

де  густина рідини;

 глибина занурення точки, у якій виміряється тиск, щодо рівня рідини в п’єзометричній трубці.

h_c = = .

Вакуумметр рідинний (зворотний п’єзометр). Являє собою вертикальну скляну трубку зі шкалою. Один кінець трубки з'єднується з місцем виміру тиску. Другий кінець трубки опущений у чашу з робочою рідиною (рис. 1.4). Умова рівності тисків, записана для поверхні , сполученої з вільною поверхнею робочої рідини в чаші, у випадку вакуумметра має вигляд:

p + _рgh_вак = р_бар.

Із цієї формули одержуємо вираження, що визначає чисельно вакуумметричну висоту

h_вак = = .

U–образний манометр. Являє собою U – образну скляну трубку зі шкалою, заповнену робочою рідиною до нульової позначки. Одна гілка манометра відкрита в атмосферу, інша з'єднана з місцем, де виміряється тиск. На рис. 1.5 (а й б) показані U–образні манометри для виміру надлишкового й вакуумметричного тисків. На рис. 1.5 (в) показаний U–образний манометр для виміру абсолютного тиску. У цьому випадку одна гілка манометра з'єднана з місцем, де виміряється тиск, а друга гілка запаяна й з її вилучене повітря (р_нп  0).

При вимірі надлишкового тиску для горизонтального рівня справедливе вираження

р_А = р_бар + _рgh,

де  різниця рівнів робочої рідини в гілках манометра.

Очевидно, що обмірюване визначає надлишковий тиск:

h = = .

При вимірі вакуумметричного тиску для горизонтального рівня n-n справедливе вираження

p_А + _рgh = p_бар.

Обмірюване є мірою вакуумметричного тиску

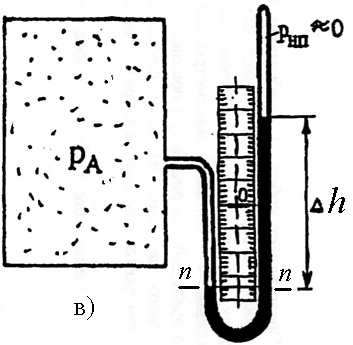
Рисунок 1.5 - U-образний манометр для виміру надлишкового (а), вакуумметричного (б) і повного (в) тисків

При вимірі абсолютного тиску в посудині (трубопроводі) для горизонтального рівня умова рівності тисків має вигляд

р_А = _рgh.

Різниця рівнів у гілках манометра є мірою абсолютного тиску в резервуарі

h = .

h = = .

Диференціальний манометр застосовується для виміру різниці тисків. Являє собою U-образний манометр, обидві гілки якого приєднуються до місць виміру тиску (рис. 1.6). Різниця тисків у розглянутих точках визначається різницею рівнів робочої рідини в гілках манометра.

Для горизонтального рівня справедливе вираження

p_А + gh = p + _рgh

або

p_А – p = (_p  )gh.

Якщо в розглянутих об'ємах, у яких виміряється різниця тисків, перебуває газ, то зміною вагового тиску в газі, що заповнює частину вимірювальної трубки, звичайно зневажають. Це, як правило, припустимо, тому що щільність газів на три порядки менше щільності рідин. Тоді умова рівності тисків горизонтального рівня приймає вид

p_А = p + _рgh.

Обмірювана різниця рівнів робочої рідини в гілках манометра є мірою різниці тисків у розглянутих точках

h = .

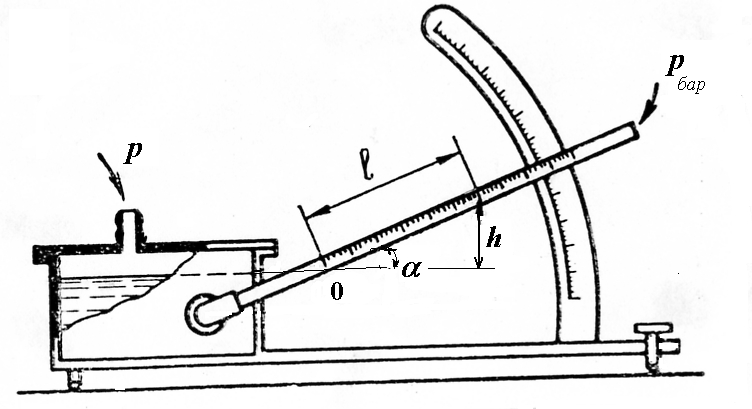
Мікроманометр застосовується для виміру тиску й різниці тисків з досить високою точністю. Являє собою чашу, заповнену робочою рідиною, з похилою трубкою й похилою шкалою (рис. 1.7). При вимірі малих тисків у газах для збільшення точності в якості робочих застосовують легкі рідини, наприклад, спирт. Показанням приладу є величина l зсуву рідини в похилій трубці.

Для рівня справедливо

p = p_бар + _рgh.

Оскільки , надлишковий тиск на поверхні рідини в чаші дорівнює

р_надл = р – р_бар = _рglsin,

де  відстань, на яку переміщається робоча рідина по шкалі приладу при вимірі;

 кут нахилу трубки до обрію.

Точність приладу зростає зі зменшенням кута нахилу трубки, тому що при цьому збільшується показання приладу, що відповідає даному тиску р. Прилади з похилою трубкою застосовують для вимірів тисків, рівних 240…1470Па.

Р исунок1.6 – Диференціальний Рисунок 1.7  Мікроманометр

манометр

Пружинні прилади

Основними перевагами пружинних приладів є:

• портативність;

• універсальність;

• простота пристрою;

• простота застосування;

• широкий діапазон вимірюваних тисків.

Основним недоліком пружинних приладів є нестабільність їхніх показань, що викликана рядом причин: поступовою зміною пружних властивостей деформованого елемента, можливим виникненням залишкової деформації в ньому, зношуванням передавального механізму.

Трубчасті пружинні прилади вимірюють тиск у межах від до 1 Па; погрішність вимірів 1...3%. Мембранні прилади застосовують для виміру вакууму й надлишкового тиску, що не перевищує 2,5 МПа.

Манометр, вакуумметр і мановакуумметр із одновитковою трубчастою пружиною (рис. 1.8). Основною деталлю приладу є зігнута в дузі окружності порожня трубка, що має в перетині овальну форму (пружина Бурдона). Один кінець трубки запаяний. Вимірюваний тиск р передається усередину трубки через другий відкритий її кінець. Під дією різниці тисків у корпусі приладу й усередині полої трубки р пружина деформується.

Якщо р  р_бар, то надлишковий тиск розгинає трубку 1, якщо р  р_бар, то трубка згинається, тому що в ній установлюється вакуумметричний тиск (розрідження). Запаяний кінець трубки, переміщаючись, пускає в хід передавальний механізм 2. Стрілка приладу переміщається щодо шкали 3, яка проградуїрована в одиницях тиску.

Прилади з мембранною пружиною. Пружним елементом мембранного приладу є мембрана 2 (рис. 1.9), що представляє собою гофровану металеву пластинку, закріплену між фланцями нижньої й верхньої частин корпуса приладу. На мембрану через канал штуцера 1 передається тиск p, під дією якого мембрана прогинається. Через передавальний механізм 3 прогин передається на стрілку приладу, що сковзає по шкалі.

1 - трубчаста пружина манометра;

2- передавальний механізм; 1 - штуцер; 2 - мембрана;

3 - шкала; 4 - штуцер 3 - передавальний механізм

Рисунок 1.8 - Пружинний манометр Рисунок 1.9 - Мембранний манометр

1.2 Опис лабораторної установки

Виміри виконуються на лабораторних установках, показаних на рис. 1.10 й 1.11. Установка, зображена на рис. 1.10, складається з напірного резервуара 1, трубопроводу 3, що підводить воду в бак, зливальної труби 2, що забезпечує постійний рівень рідини Н у резервуарі, трубопроводу змінного перетину 4, що регулюється краном 5. У вертикальній стінці напірного бака зроблено отвір, до якого приєднаний насадок (точка А), статичний напір у точках В і С вимірюють через отвори в стінці трубопроводу, постачених патрубками, які з'єднані з п’єзометрами.

Установка на рис. 1.11 являє собою комбіновану мережу, що складається з вентилятора й двох ділянок: одна ділянка мережі знаходиться зі сторони всмоктування, інша – з боку нагнітання. На цих ділянках у точках D й E установлені рідинні U–образні манометри.

1 - напірний резервуар; 2 - зливальна труба; 3 - трубопровід, що підводить воду; 4 - трубопровід змінного перетину; 5 - регулюючий кран

Рисунок 1.10 - Схема лабораторної установки

1 - всмоктувальна ділянка мережі; 2 - вентилятор; 3 - нагнітальна ділянка мережі

Рисунок 1.11 - Схема комбінованої мережі

1.3 Порядок виконання лабораторної роботи

1. Видалити повітря з рідини, що заповнює п’єзометри й сполучні трубки. Для цього на сполучних трубках приладів передбачені триходові крани. Заповнити U-образні манометри робочою рідиною до нуля шкали.

2. При закритому крані 5 виміряти показання п’єзометрів.

3. Виміряти відстань від центра отвору, до якого приєднаний насадок (точка А) до осі горизонтального трубопроводу змінного перетину Н.

4. Висоту Н₁ над центром отвору насадка визначити як різницю показань п’єзометрів при закритому крані й висоті Н.

5. Визначити атмосферний тиск по барометрові.

6. Визначити температуру води .

7. Відкрити кран 5. При сталій витраті рідини виміряти показання п’єзометрів.

Всі дані занести в табл. 1.1.

Таблиця 1.1 – Результати вимірів у точках А, В, С

8. Визначити температуру повітря .

9. Включити вентилятор і зняти показання U-образних манометрів. Результати вимірів внести в таблицю 1.2.

Таблиця 1.2 - Результати вимірів у точках Д, Е

1.4 Обробка результатів вимірів

Використовуючи рівняння (1.1), (1.2 а) і (1.3) визначити повний й надлишковий (або вакуумметричний) тиск у точках А, В, С, Д и Е. Результати розрахунків представити у вигляді табл. 1.3.

Таблиця 1.3 - Результати розрахунків

Зміст звіту

1. Короткі теоретичні відомості.

2. Схема лабораторних установок й їхній опис.

3. Таблиці вимірів і результатів розрахунків 1.1, 1.2 й 1.3.

4. Висновок.

Контрольні питання

1. Закон Паскаля, наслідок з нього.

2. Основний гідростатичний закон. Поняття абсолютного, вакуумметричного й надлишкового тиску. Одиниці виміру тиску.

3. Класифікація приладів для виміру тиску. Їхні основні характеристики.

4. Принцип дії приладів для виміру тиску.

5. Пристрій рідинних приладів для виміру тиску. Їхні переваги й недоліки. Діапазон роботи.

6. Пристрій пружинних приладів для виміру тиску. Їхні переваги й недоліки. Діапазон роботи.

7. Які способи збільшення ступеня точності рідинних приладів?

Лабораторна робота № 2

Вивчення режимів руху рідини

Мета роботи: Вивчити режими руху рідини на установці Рейнольдса.

2.1 Загальні відомості

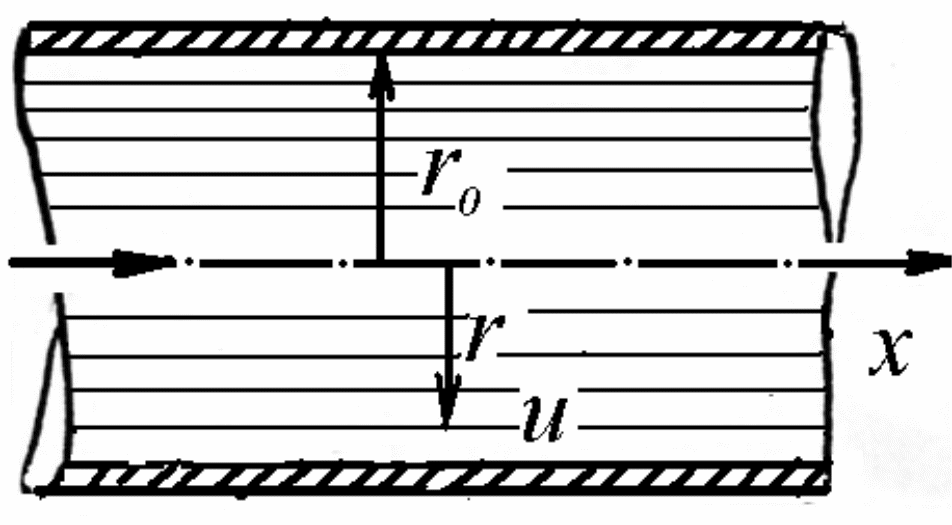
В даний момент часу в кожній точці в межах потоку, що рухається, перебуває частка рідини, що має деяку швидкість u. Ця швидкість називається миттєвою місцевою швидкістю. Сукупність миттєвих місцевих швидкостей представляє векторне поле, що називається полем швидкостей.

За характером зміни поля швидкостей у часі рух рідини ділиться на неусталений й усталений.

Неусталений (нестаціонарний) рух такий, при якому в точках області, де рухається рідина, місцеві швидкості змінюються із часом. При неусталеному русі всі елементи руху (швидкість u, прискорення j, тиск p, глибина h) є функцією й координат (x, y, z) і часу t.

Якщо в будь-якій точці потоку рідини швидкість, тиск і прискорення залишаються постійними, тобто не змінюються в часі ні по величині, ні по напрямку, то такий рух розглядається як усталений (стаціонарний).

Усталений рух може бути рівномірним і нерівномірним.

Рівномірним називається такий усталений рух, при якому живі перетини потоку й середня швидкість v у них однакові по його довжині.

Нерівномірним називається такий усталений рух рідини, при якому живі перетини й середні швидкості потоку v змінюються по його довжині.

Якщо потік з усіх боків обмежений твердими стінками, то він називається напірним. Якщо тільки частина потоку обмежена твердими стінками, а на іншій частині рідина граничить із газом, зокрема, з атмосферою (потік має вільну поверхню), то такий рух називається безнапірним.

Живим перетином потоку  називають поперечний переріз потоку, перпендикулярний його напрямку.

Об'ємною витратою потоку Q називають об'єм рідини V, що проходить в одиницю часу t через живий перетин потоку, (м³/с):

Q = (2.1)

Змочений периметр  (хі) – частина периметра живого перетину, на якому рідина стикається із твердими стінками.

Гідравлічним радіусом R називають відношення площі живого перетину потоку  до змоченого периметра 

R= (2.2)

Відношення чотирьох площ живого перетину потоку до змоченого периметра називається діаметром еквівалентним d_екв

d_екв = = 4R (2.3)

Середньою швидкістю v потоку в даному перетині називають відношення об'ємної витрати потоку Q до площі його живого перетину 

v = (2.4)

Втрати енергії при русі рідини залежать від режиму руху.

Розрізняють два режими руху рідини: ламінарний і турбулентний (табл. 2.1).

Рух рідини, при якому відсутні зміни (пульсації) місцевих швидкостей, що приводять до перемішування рідини, називають ламінарним (від латинського слова lamina – шар, пластинка).

Рух рідини, при якому відбуваються зміни (пульсації) місцевих швидкостей, що приводять до перемішування рідини називають турбулентним (від латинського слова turbulentus – безладний, бурхливий).

Рейнольдс установив, що перехід від ламінарного плину до турбулентного й навпаки визначається середньою швидкістю плину v, характерним поперечним розміром потоку L, фізичними властивостями рідини: щільністю  і в'язкістю (динамічний коефіцієнт в'язкості  або кінематичний коефіцієнт в'язкості ). У загальному випадку режим руху рідини визначається безрозмірним комплексом, складеним із зазначеним величин і називаним числом (критерієм) Рейнольдса

Re = = (2.5)

Число Рейнольдса характеризує відношення сил інерції до сил тертя (в'язкості). Перехід від одного режиму руху в іншій порозумівається перевагою сили інерції або сили тертя.

У якості характерного геометричного розміру живого перетину потоку L найчастіше приймають діаметр труби d (для круглих напірних труб), для не круглих і безнапірних труб гідравлічний радіус R або діаметр еквівалентний . Тоді, відповідно

Re_d = , = , Re_{d экв} =

Таблиця 2.1 - Основні відмінності ламінарного й турбулентного плину (рух в трубі круглого перетину)

Швидкість потоку, при якій відбувається зміна режиму руху рідини, називається критичною. Рейнольдс виявив існування двох критичних швидкостей: верхньої критичної швидкості – при переході ламінарного режиму руху в турбулентний, і нижньої критичної швидкості – при переході турбулентного режиму руху в ламінарний. Відповідно розрізняють верхнє й нижнє критичні числа Рейнольдса.

0 Re

Для круглих напірних труб при усталеному рівномірному русі рідини =2000…2320, а = 4000…100000.

Значення (перехід ламінарного плину в турбулентний) залежить від зовнішніх умов досліду: сталості температури, рівня вібрації установки, умов входу в трубку, шорсткості поверхні стінок труби, стану рідини в резервуарі, що живить трубу й т.п. Значення (перехід турбулентного руху в ламінарний) від цих величин практично не залежить.

У практичних умовах, де завжди є джерела випадкових збурювань, варто зважати тільки на нижню границю.

Таким чином, як критичне число Рейнольдса прийняте для циліндричних напірних труб

Re_кр = = 2000…2320

Для будь-якого потоку по відомим v, L й  можна обчислити число Рейнольдса й зрівняти його із критичним значенням Re_кр. Якщо Re  Re_кр, то v  v_кр і режим руху рідини ламінарний; якщо Re  Re_кр, то v  v_кр і режим руху турбулентний.

У природі й техніці турбулентний рух рідини спостерігається частіше, ніж ламінарний. Області ламінарного руху:

• рух дуже в’язких рідин типу масел по трубах і механізмах;

• рух ґрунтових вод (але він може бути також і турбулентним);

• рух у капілярах (у тому числі й рух крові в живих організмах).

2.2 Опис лабораторної установки

Установка, що зображена на рис. 2.1, призначена для візуального спостереження режиму плину рідини.

1 - резервуар (бак); 2 - скляна трубка; 3 - кран для регулювання витрати потоку; 4 - мірний бак; 5 - трубка для подачі підфарбованої рідини; 6 - посудина з розчином підфарбованої рідини; 7 - кран для регулювання подачі підфарбованої рідини; 8 - кран на мірному баці

Рисунок 2.1 - Установка Рейнольдса для вивчення режимів руху рідини

У циліндричну скляну трубку через плавний коноїдальний вхід рідина подається з резервуара 1, де вона заспокоюється за допомогою системи ґрат. Резервуар (бак) 1 досить великого розміру. Висота рівня рідини в баці підтримується постійною. Наприкінці скляної труби 2 установлений кран 3 для регулювання витрати потоку. Вимір витрати виконується за допомогою мірного бака 4 і секундоміра.

У вхідну ділянку труби через тонку трубочку 5 з посудини 6 подається підфарбована рідина із щільністю й швидкістю витікання, близькими до цих же характеристик потоку рідини в трубі. Витрата фарби регулюється краном 7. Підфарбований струмок рідини дозволяє зробити видимою структуру потоку в трубі.

При невеликих значеннях швидкості v підфарбований струмок має вигляд нитки із чітко обкресленими границями. Рідина рухається окремими шарами, що не перемішуються (рис. 2.2 а).

Рисунок 2.2 - Ламінарний (а) і турбулентний (б, в) рух рідини

При більших швидкостях підфарбований струмок починає викривлятися й стає хвилеподібним (рис. 2.2 б). Це відбувається в результаті змін у часі (пульсації) векторів місцевих швидкостей у потоці.

Наявність поперечних пульсацій є відмітною рисою турбулентного плину. Тому поява поперечних коливань пофарбованого струмка рідини служить вказівкою на перехід ламінарного режиму в турбулентний.

При подальшому збільшенні швидкості потоку струмок розпадається на окремі добре видні вихри, відбувається перемішування пофарбованого струмка з усією масою поточної рідини. На невеликій відстані від входу (10-20 діаметрів труби) потік виявляється рівномірно пофарбованим (рис. 2.2 в).

2.3 Порядок виконання лабораторної роботи

1. При закритому крані (3) заповнюють напірний бак водою так, щоб безупинно працював злив.

2. Злегка відкривши вентиль (3), створюють невелику витрату води по трубі (кран (8) на мірному бачку відкритий).

3. Відкриттям крана (7) домагаються одержання тонкого струмка фарби, що не розривається. За візуальними спостереженнями встановлюють ламінарний режим.

4. При даному режимі руху рідини закривають кран (8) на мірному баці. Замірять висоту підйому рідини в мірному бачку h за відповідний час t.

5. За допомогою крана (8) установлюють за візуальними спостереженнями турбулентний режим і повторюють виміри (3...4 рази).

6. Термометром замірять температуру води й по таблиці (дод. В) визначають значення коефіцієнта кінематичної в'язкості води .

Результати вимірів заносять у таблицю 2.2.

Таблиця 2.2 - Результати вимірів і довідкові величини

2.4 Обробка результатів експерименту

1. Визначають об'єм води V, що витекла в мірний бачок за час t при і-м вимірі, м³:

V = h_i  _б,

де h – висота підйому води в мірному бачку при і-м вимірі, м;

- площа перетину мірного бачка, м².

2. Визначають об'ємну витрату Q при і-м вимірі, м³/с:

Q = ,

де t – час наповнення мірного бака, c.

3. Визначають середню швидкість руху води по трубі v при і-м вимірі з рівняння сталості об'ємної витрати, м/с:

v = = ,

де  - площа поперечного переріза труби, м².

4. Розраховують число Рейнольдса:

Re = .

5. Розраховане значення критерію Рейнольдса порівнюють із критичним й

роблять висновок про режим плину рідини (з розрахунку).

6. Побудувати графік залежності Re = f(v) і визначити критичну швидкість переходу з ламінарного режиму руху в турбулентний.

7. Результати розрахунку зводять у таблиці 2.3.

Таблиця 2.3 - Результати розрахунків

Зміст звіту

1. Короткі теоретичні відомості.

2. Схема лабораторної установки та її опис.

3. Таблиці вимірів і розрахунків.

4. Графік залежності Re = f(v).

5. Висновок.

Контрольні питання:

1. Режими руху та їхні особливості.

2. Критерій Рейнольдса та його фізичний зміст.

3. Поняття характерного розміру трубопроводу, напруги.

4. Поняття усталеного й неусталеного руху.

5. Поняття рівномірного й нерівномірного руху.

Лабораторна робота № 3

ГРАФІЧНА ІЛЮСТРАЦІЯ РІВНЯННЯ БЕРНУЛЛІ

Мета роботи: Експериментально перевірити й графічно проілюструвати рівняння Бернуллі.

3.1 Загальні відомості

З погляду енергетичного змісту рівняння Бернуллі формулюється так: при русі нев'язкої нестисливої рідини уздовж потоку сума питомих енергій – потенційної (положення й тиску) і кінетичної – є величина постійна. Рівняння Бернуллі являє собою закон збереження механічної енергії при русі ідеальної рідини.

При формулюванні рівняння Бернуллі використаємо поняття питомої енергії, тобто енергії рідини, віднесеної до одиниці ваги рідини.

Геометричний зміст рівняння Бернуллі: при русі нев'язкої нестисливої рідини уздовж потоку сума геометричної, п’єзометричної і швидкісної висот є величиною постійною.

Рівняння Бернуллі записується у вигляді

= const, (3.1)

де  щільність рідини, кг/м³;

р – манометричний тиск у центрі розглянутого перетину потоку, Па;

 коефіцієнт Кориоліса (коефіцієнт кінетичної енергії), що характеризує нерівномірність розподілу швидкостей по перетині потоку;

v – середня по перетині потоку швидкість руху рідини, м/с;

g – прискорення сили ваги, м/с².

З погляду енергетичного змісту рівняння:

z – питома потенційна енергія положення;

 питома потенційна енергія тиску;

 питома кінетична енергія;

 повна питома енергія.

Напір – лінійна величина, що виражає питому (віднесену до одиниці ваги) енергію потоку рідини в даній точці (або в даному перетині). Тоді:

 п’єзометричний напір, м;

 динамічний напір, м;

 гідродинамічний (або повний) напір, м.

С точки зору геометричного змісту рівняння:

z – геометрична висота, м;

 п’єзометрична висота, м;

 швидкісна (або динамічна висота), м;

 повна висота рідини в перетині, м.

Напишемо рівняння Бернуллі для трубопроводу, що складається із труб різних діаметрів (рис. 3.1). При горизонтальному розташуванні трубопроводу (z₁ = z₂) рівність питомих енергій для розрахункових перетинів 1-1 й 2-2 виражається рівнянням виду

= . (3.2)

При переході потоку з вузької частини трубопроводу в широку спостерігається ріст питомої потенційної енергії за рахунок зменшення кінетичної енергії потоку .

Наведені вище рівності (3.1) і (3.2) виконуються тільки для ідеальної (нев'язкої) рідини. При експериментальній перевірці рівняння Бернуллі з'ясовується, що повна питома енергія потоку реальної (в'язкої) рідини в попередньому перетині завжди більше чим надалі в напрямку руху рідини. Різниця між повними питомими енергіями на початку й в кінці розглянутої ділянки визначає втрати питомої енергії (напору) h_втр, на подолання опорів у трубопроводі. Рівняння Бернуллі для реальної (в'язкої) рідини (при = = 1) має вигляд

= + h_втр.

Гідравлічним ухилом i називається відношення втрат напору до довжини ділянки l, на якій ці втрати відбуваються (тобто втрати на одиницю довжини), м/м:

i = .

Гідравлічний ухил завжди позитивний, тому що повний напір реальної рідини завжди зменшується уздовж руху.

П’єзометричним ухилом називається віднесена до одиниці довжини зміна п’єзометричного напору . П’єзометричний ухил вважається позитивним, якщо за течією п’єзометрична лінія знижується.

3.2 Схема лабораторної установки

Лабораторна установка включає горизонтальний трубопровід змінного перетину, напірний бак і мірний бак. На трубопроводі встановлені п’єзометри. Експериментальна установка схематично зображена на рис. 3.1

АВ, СD – вузькі ділянки трубопроводу (d = 0,020 м); ВС – широка ділянка трубопроводу (D = 0,1 м).

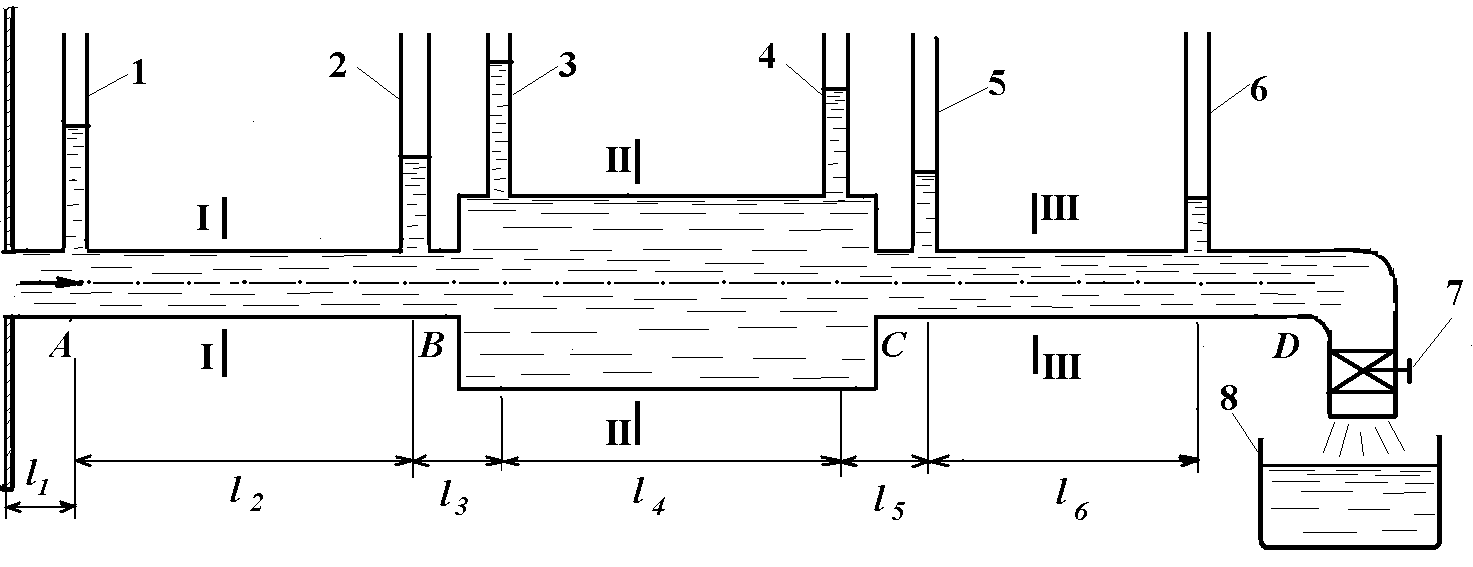
1...6 - п’єзометри; 7 - регулюючий кран; 8 - мірний бачок.

Рисунок 3.1 - Схема установки

3.3 Порядок проведення роботи

Підготувавши установку до роботи, регулюючим краном установлюють певну витрату води, що протікає по трубопроводу. При даному режимі записують показання п’єзометрів, а також заміряють висоту рідини h_i, що заповнила мірний бачок за час t.

Змінюючи за допомогою регулюючого крана витрату води по трубопроводу, повторюють зазначені виміри ще два рази. Результати вимірів заносять у табл. 3.1.

Таблиця 3.1 - Результати вимірів

3.4 Обробка результатів експерименту

Розрахунком визначають об'ємну витрату води для кожного з дослідів, м³/с

Q_j = = ,

де V  об'єм мірного бака, м³;

h_j – висота підйому води в мірному баці при j - тім вимірі, м;

 площа перетину мірного бака, м²;

t – час заповнення мірного бака, с.

Для кожного з дослідів розраховують швидкість потоку (v = = ) і швидкісну (динамічну) висоту для перетинів 1-1, 2-2, 3-3. Підсумовуючи відповідні значення п’єзометричної і швидкісної висот, одержують значення повної висоти (повного напору) у розрахункових перетинах горизонтального (z₁ = z₂) трубопроводу.

Результати розрахунків вносять у табл. 3.2.

Таблиця 3.2 - Результати вимірів і розрахунків

На міліметровий папір наносять координатні осі. Вісь абсцис відповідає площині порівняння, а вісь ординат - внутрішній стороні стінки напірного бака.

На осі абсцис в обраному масштабі відзначають положення перетинів, у яких установлені п’єзометри (відстань від стінки напірного бака до першого п’єзометра l₁ і відстані між п’єзометрами (l₂…l₆).

На осі ординат відзначають висоти в кожному перетині: геометричну (z_i), п’єзометричну й швидкісну . Якщо площина порівняння сполучена з віссю горизонтального трубопроводу, то z_i = 0. Графічно зміна по довжині трубопроводу п’єзометричного напору є п’єзометричною лінією. П’єзометрична лінія відокремлює область зміни потенційної енергії від області зміни кінетичної енергії. Лінія, що з'єднує кінці відрізків - є гідродинамічною лінією. Провівши лінію повного напору для ідеальної рідини Н_ід, з графіка знаходять втрати напору h_втр.

Розраховують п’єзометричний ухил i_n для окремих ділянок п’єзометричної лінії:

i_{п 1-2} = ,

i_{п 2-3} = і т.д.

Гідравлічний ухил i, що характеризує зміну повного напору по довжині трубопроводу в напрямку руху рідини, розраховується для ділянок з постійним діаметром (d = const): l₂, l₄, l₆:

i_1-2 = = ;

i_3-4 =

i_5-6 =

Аналізують перетворення енергії, що мають місце при русі води по трубопроводу змінного перетину.

Зміст звіту

1. Короткі теоретичні відомості.

2. Схема лабораторної установки і її опис.

3. Таблиця вимірів.

4. Таблиця розрахунків.

5. Графік зміни п’єзометричного й повного напору.

6. Висновок.

Контрольні питання

1. Який закон виражає рівняння Бернуллі?

2. Написати рівняння Бернуллі для потоку реальної (ідеальної) рідини. Пояснити.

3. Пояснити фізичний зміст величин z, , .

4. Геометричний й енергетичний зміст рівняння Бернуллі для ідеальної й реальної рідини.

5. Що характеризує п’єзометричний ухил i_п? Гідравлічний ухил i?

Лабораторна робота № 4

ВИЗНАЧЕННЯ КОЕФІЦІЄНТА ГІДРАВЛІЧНОГО ТЕРТЯ

Мета роботи: Вивчити залежність коефіцієнта гідравлічного тертя від числа Рейнольдса.

4.1 Загальні теоретичні відомості

При русі реальної рідини частина енергії потоку губиться на подолання сил тертя. Втрати питомої енергії (напору) на ділянці між двома довільно обраними перетинами 1-1 й 2-2 визначають із рівняння Бернуллі, м:

h_тр = Н_{Р 1}  Н_{Р 2} = 

Для горизонтальної труби постійного діаметра при одержують:

h_тр = 

Втрати напору по довжині (лінійні втрати) h_тр визначаються формулою Дарсі-Вейсбаха, м:

h_тр =   , (4.1)

де  коефіцієнт гідравлічного тертя (коефіцієнт Дарсі);

 довжина й діаметр трубопроводу відповідно, м;

v – середня швидкість плину рідини в перетині потоку, м/с.

Коефіцієнт гідравлічного тертя залежить від в'язкості й щільності рідини , діаметра трубопроводу d, шорсткості внутрішніх стінок трубопроводу k_е й середньої швидкості руху рідини v. У загальному випадку коефіцієнт залежить від двох безрозмірних параметрів – числа Рейнольдса Re і відносної шорсткості :

 = f ,

де  абсолютна еквівалентна шорсткість стінок труби, м (дод. Г).

Під абсолютною еквівалентною шорсткістю розуміють таку уявлювану (умовну) рівномірну шорсткість, при якій втрати напору дорівнюють втратам у реальному трубопроводі за тих самих умов плину.

При ламінарному режимі плину рідини (ReRe_кр) коефіцієнт гідравлічного тертя залежить тільки від числа Рейнольдса й визначається по формулі:

 = (4.2)

По найпоширенішій гіпотезі Прандтля турбулентний потік (ReRe_кр) ділять на турбулентне ядро й в’язкий підшар. Товщина в’язкого підшару залежить від числа Рейнольдса. При відносно невеликих швидкостях (невеликих числах Re) в’язкий підшар повністю закриває всі виступи шорсткості стінки (рис. 4.1, а). В результаті вплив шорсткості на коефіцієнт гідравлічного тертя й, відповідно, на втрати напору по довжині буде зневажливо малий. Ця зона турбулентного руху рідини називається зоною гідравлічно гладких труб. Критерій зони турбулентності менше 10. Коефіцієнт гідравлічного опору визначається по формулі Блазіуса:

 = (4.3)

Рисунок 4.1 – Гідравлічна шорсткість

Зі збільшенням числа Рейнольдса товщина в’язкого підшару зменшується, і вплив виступів шорсткості на втрати напору збільшується (рис. 4.1, б). У цій зоні змішаного опору, тобто області переходу від гідравлічно гладких до гідравлічно шорсткуватих труб коефіцієнт залежить і від числа Рейнольдса й від відносної шорсткості. Критерій зони турбулентності перебуває у межах від 10 до 500. Коефіцієнт Дарсі визначають по формулі Альтшуля:

 = 0,11 (4.4)

При дуже великих числах Рейнольдса в’язкий підшар стає зникаюче малим й турбулентне ядро потоку захоплює виступи шорсткості стінок (рис. 4.1, в). У цій зоні гідравлічно шорсткуватих труб коефіцієнт залежить тільки від відносної шорсткості внутрішніх стінок трубопроводу. Критерій зони турбулентності більше 500. Коефіцієнт визначають по формулі Шифринсона:

 = 0,11 (4.5)

4.2 Схема експериментальної установки

Схема експериментальної установки схематично показана на рис. 4.2. По трубопроводу 1 вода з напірного бака випливає в мірний бачок 3. На початку й кінці ділянки трубопроводу довжиною встановлені п’єзометри, за допомогою яких у досліді визначаються втрати напору h_тр. Кран 2 служить для регулювання витрати води.

Рисунок 4.2 - Схема експериментальної установки

4.3 Порядок проведення роботи

Заповнюють напірний бак водою до постійного рівня; видаляють пухирці повітря з п’єзометричних трубок. За допомогою регулюючого крана встановлюють певну витрату води. При заданій витраті тричі знімають показання п’єзометрів і визначають час заповнення мірного бачка. Проводять ще два досліди при інших витратах води.

Результати вимірів зводять у табл. 4.1.

Таблиця 4.1 - Результати вимірів і довідкові дані

4.4 Обробка результатів експерименту

Об'ємна витрата води, що витекла із труби за час t, дорівнює, м³/с:

Q = = ,

де t – час заповнення мірного бачка, с;

V  об’єм мірного бачка, м³.

Середню швидкість руху води в перетині потоку можна виразити через об'ємну витрату Q, м/с:

v = = ,

де  площа живого перетину труби, м².

По різниці показань п’єзометрів визначають втрати напору h_тр на ділянці потоку. З урахуванням величини h_тр із формули Дарсі-Вейсбаха (4.1) знаходять експериментальне значення коефіцієнта гідравлічного тертя:

 = h_тр.

При визначенні розрахункового (теоретичного) значення коефіцієнта гідравлічного тертя попередньо по середній швидкості руху води в трубі v розраховують число Рейнольдса

Re = ,

де - кінематичний коефіцієнт в'язкості для води, (додаток В).

У випадку турбулентного плину визначають критерій зони турбулентності . Значення абсолютної еквівалентної шорсткості k_е приймають відповідно до додатка Г.

Залежно від чисельного значення числа Рейнольдса й критерію зони турбулентності визначають розрахункові значення коефіцієнта гідравлічного тертя по формулах (4.2)…(4...5).

У розрахунках враховують усереднені дані по кожному досліду.

Результати розрахунків зводять у табл. 4.2.

Таблиця 4.2 - Результати розрахунків

Зміст звіту

1. Короткі теоретичні відомості.

2. Схема лабораторної установки і її опис.

3. Таблиця вимірів.

4. Таблиця розрахунків.

5. Висновок.

Контрольні питання

1. Напишіть формулу Дарсі-Вейсбаха. Поясніть.

2. Як варто розуміти терміни «гідравлічно гладкі» й «гідравлічно шорсткуваті» труби?

3. Як варто розуміти природну абсолютну, абсолютну еквівалентну, відносну шорсткість внутрішніх стінок труби?

4. Від чого залежить коефіцієнт гідравлічного опору при ламінарному режимі? При турбулентному русі рідини?

5. Назвіть зони гідравлічних опорів. Чим вони розрізняються?

Лабораторна робота № 5

ВИЗНАЧЕННЯ КОЕФІЦІЄНТІВ МІСЦЕВИХ ОПОРІВ

Мета роботи: Експериментально визначити коефіцієнти місцевих опорів.

5.1 Загальні відомості

Місцевими опорами називають короткі ділянки потоку, на яких вектор середньої швидкості змінюється по величині й (або) напрямку. У місцевих опорах мають місце додаткові втрати напору, які визначаються по формулі Вейсбаха, м

h_м =  (5.1)

де v – середня швидкість у перетині, зазвичай за місцевим опором, м/с;

 – коефіцієнт місцевого опору, безрозмірний;

g – прискорення сили ваги, м/с².

До місцевих опорів належать діафрагми, крани, засувки, повороти, раптові звуження й розширення трубопроводу й ін.

У загальному випадку коефіцієнт місцевого опору  залежить від типу місцевого опору, ступеня стиснення потоку й від числа Рейнольдса. При розвиненому турбулентному режимі плину в автомодельній області коефіцієнт  від числа Рейнольдса практично не залежить.

Коефіцієнт місцевого опору  можна визначити з рівняння Вейсбаха (5.1), експериментально вимірявши втрати напору в місцевому опорі й середню швидкість руху в перетині потоку. Втрати напору знаходять, використовуючи рівняння Бернуллі для двох розрахункових перетинів (1-1 до й 2-2 після місцевого опору), м

h_м =  ,

де z₁, z₂ – геометричні висоти в прийнятих перетинах потоку, м;

,  п’єзометричні висоти в прийнятих перетинах потоку, м;

₁ , ₂  швидкісні висоти в прийнятих перетинах потоку, м.

Розрахункові перетини варто вибирати так, щоб вони перебували досить близько від місцевого опору, і можна було зневажити втратами напору на тертя.

Для горизонтальної труби постійного діаметра втрати напору в місцевому опорі дорівнюють різниці показань п’єзометрів, м

h_м =  .

З урахуванням місцевих втрат напору з формули (5.1) розраховують експериментальний коефіцієнт місцевого опору 

= h_м (5.1, а)

Для турбулентного потоку при раптовому розширенні для швидкості до розширення v₁ (у трубопроводі меншого перетину) розрахунковий коефіцієнт місцевого опору можна визначити по формулі

_{р. р. 1} = = (5.2)

де ₁  площа перетину трубопроводу до місцевого опору, м²;

₂  площа перетину трубопроводу після місцевого опору, м²;

n_р =  ступінь розширення потоку. Ступінь розширення потоку n_р являє собою відношення площі трубопроводу більшого перетину ₂ (після місцевого опору) до площі трубопроводу меншого перетину ₁ (до місцевого опору).

Для швидкості після раптового розширення v₂ коефіцієнт місцевого опору можна визначити по формулі

_{р. р. 2} = = (5.3)

У випадку раптового звуження потоку розрахунковий коефіцієнт місцевого опору може бути розрахований по емпіричній формулі

_{р. зв.} = (5.4 а)

де  - коефіцієнт стиску струменя, дорівнює відношенню мінімального живого перетину потоку _п до площі трубопроводу меншого перетину ₂ (після місцевого опору)  = .

Коефіцієнт стиску струменя  залежить від ступеня стиску потоку n_с і його можна оцінити по емпіричній формулі:

 = 0,57 + (5.4 б)

Ступінь стиску потоку n_с являє собою відношення площі трубопроводу меншого перетину ₂ (після місцевого опору) до площі трубопроводу більшого перетину ₁ (до місцевого опору):

n_с = . (5.4 в)

Коефіцієнт місцевого опору при плавному повороті труби на 90⁰ визначають по емпіричній формулі Альтшуля:

₉₀ = (5.5)

де d – діаметр трубопроводу, м;

R_п – радіус закруглення труби, м;

  коефіцієнт гідравлічного тертя.

5.2 Опис експериментальної установки

Схематично експериментальна установка представлена на рис. 5.1. Вона складається із трубопроводу змінного перетину 1, який регулюється краном 8, і мірного бачка 9. Це дозволяє визначити коефіцієнт місцевого опору при раптовому розширенні I, раптовому звуженні II, на вентилі III і повороті потоку IV. Для визначення втрат напору до й після кожного місцевого опору встановлені п’єзометри 2...7.

1 - трубопровід змінного перетину; 2...7 - п’єзометри; 8 - регулюючий кран;

9 - (мірний бак)

Рисунок 5.1 - Схема установки

5.3 Порядок проведення роботи

Заповнюють напірний бак водою до постійного рівня, видаляють пухирці повітря з п’єзометрів. За допомогою регулюючого крана встановлюють певну витрату води. Знімають і записують показання п’єзометрів; за секундоміром визначають час заповнення мірного бачка. Дослід повторюють при інших витратах води.

Результати вимірів заносять у табл. 5.1.

Таблиця 5.1 - Результати вимірів і довідкові величини

5.4 Обробка результатів експерименту

Об'ємну витрату води, що витікає, знаходять по формулі, м³/с:

Q = = ,

де V  об’єм мірного бачка, м³;

t – час заповнення мірного бачка, с;

Середня швидкість у перетині потоку може бути визначена з рівняння сталості об'ємної витрати, Q, м/с:

v = = ,

де  площа перетину потоку в трубопроводі, м².

З урахуванням втрат напору у відповідних місцевих опорах розраховують значення коефіцієнта. Для раптового розширення, раптового звуження й повороту потоку експериментальні значення коефіцієнтів, що розраховані по формулі (5.1, а), зіставляють із розрахованими по теоретичних формулах (5.2)...(5.5). Результати розрахунку зводять у табл. 5.2.

Зміст звіту

1. Короткі теоретичні відомості.

2. Схема лабораторної установки і її опис.

3. Таблиця вимірів.

4. Таблиця розрахунків.

5. Висновок.

Таблиця 5.2 - Результати розрахунків

Контрольні питання

1. Що називають місцевим опором? Приведіть приклади місцевих опорів.

2. Від яких параметрів залежать втрати напору в місцевих опорах?

3. Як визначити коефіцієнт місцевого опору експериментально?

4. Втрати напору при раптовому розширенні потоку.

5. Як розраховують втрати напору при раптовому звуженні потоку?

6. Втрати напору при повороті потоку.

Лабораторна робота № 6

ВИТІКАННЯ РІДИНИ ЧЕРЕЗ ОТВОРИ Й НАСАДКИ

ПРИ ПОСТІЙНОМУ НАПОРІ

Мета роботи: Експериментально визначити коефіцієнти витрати, швидкості, опору й стиску для отворів і насадків різних типів.

6.1 Загальні відомості

В техніці широко застосовується витікання рідини через різні отвори й насадки. Розрізняють витікання через малий отвір у тонкій стінці й через насадки різних видів.

Отвір називається малим, якщо у всіх його точках геометричний напір Н и швидкості практично однакові. Звичайно приймають отвір малим, якщо його найбільший вертикальний розмір S  0,1 Н. Тонкою називають стінку, якщо її товщина не впливає на умови витікання. Рідина, що витікає, торкається тільки кромки отвору. Це може бути забезпечено або при товщині стінки (0,2…0,5)d, або зрізом кромок під гострим кутом (при   3d). Насадком називається короткий патрубок певної форми, що прикріплюється до отвору в стінці для зміни характеристик стікаючого струменя в порівнянні з витіканням з отвору. Звичайно насадки мають довжину три-п'ять діаметрів отвору l(3...5)d.

Витікаючи через отвір, струмінь на деякій відстані від нього l(0,5...1)d стискується і його перетин стає менше перетину отвору. Відношення площі перетину стислого струменя _c до площі перетину отвору _о називається коефіцієнтом стиску струменя 

 = (6.1)

Швидкість витікання рідини v з отвору або через насадок дорівнює, м/с:

v =  =   (6.2)

де Н – постійний напір води в напірному баці, м;

_с  коефіцієнт Кориоліса. Звичайно приймають _с  1;

  коефіцієнт місцевого опору отвору, насадка;

  коефіцієнт швидкості.

 = = (6.3)

Коефіцієнт швидкості  характеризує зменшення швидкості витікання через отвір або насадок реальної рідини в порівнянні зі швидкістю витікання в тих же умовах ідеальної рідини. Зменшення швидкості відбувається внаслідок втрат напору при проходженні рідини через отвір, а також внаслідок втрат напору, що мають місце при розширенні стислого струменя. Чисельно коефіцієнт швидкості визначається як відношення дійсної швидкості витікання реальної рідини до теоретичної швидкості, що характеризує витікання ідеальної рідини

 = = ,

де v_max – максимальна (теоретична) швидкість витікання ідеальної рідини з отвору або з насадка. v_max = .

Витрата рідини, що випливає через отвір або насадок, визначається формулою, м³/с

Q =   , (6.4)

де   коефіцієнт витрати;

  площа перетину отвору в стінці або площа перетину вихідного отвору насадка, м².

Коефіцієнт витрати  характеризує зменшення витрати через отвір або насадок реальної рідини в порівнянні з витратою в таких же умовах ідеальної рідини.

Коефіцієнт витрати  дорівнює добутку коефіцієнта стиску струменя  і коефіцієнта швидкості 

 =  (6.5)

Коефіцієнт витрати дорівнює відношенню дійсної витрати, що відповідає витіканню реальної рідини, до теоретичної (максимальної) витрати витікання в таких же умовах ідеальної рідини

 = = .

Таким чином, витікання рідини через отвори й насадки характеризується коефіцієнтами , , , , знаючи які можна по відомих величинах d і Н обчислити швидкість витікання рідини і її витрату.

Для турбулентного руху води (автомодельна область) у табл. 6.1 наведені довідкові дані за коефіцієнтами стиску, швидкості й витрати при витіканні через отвори й насадки різних типів.

Таблиця 6.1 - Значення коефіцієнтів, що характеризують витікання

6.2 Опис експериментальної установки

Схема експериментальної установки представлена на рис. 6.1. Установка складається з напірного бака 1, у вертикальній стінці якого зроблено кілька отворів і до них приєднані насадки 3 різних видів. Насосом 6 вода безупинно подається в напірний бак 1, у якому за допомогою переливу 2 підтримується постійний рівень води. Струмінь, що випливає через отвір або насадок за допомогою лійки 4 з гумовим шлангом відводиться в мірний бачок 5.

1 - напірний бак; 2 - перелив; 3 - насадки; 4 - лійка; 5 - мірний бачок; 6 – насос

Рисунок 6.1 - Схема установки

6.3 Порядок проведення роботи

Наповнюють напірний бак водою до постійного рівня. Відкривши отвір або насадок, підводять під струмінь води прийомну лійку, гумовий шланг якої опущений у мірний бачок. Користуючись секундоміром, заміряють час заповнення мірного бачка.

Для кожного типу отворів і насадків проводять не менш трьох вимірів. У розрахунках ураховують середні значення часу заповнення бачка.

Дані вимірів і результати розрахунків зводять у табл. 6.2, 6.3.

6.4 Обробка результатів експерименту

Для кожного виміру розраховують витрату рідини при витіканні, м³/с:

Q = ,

де V – об’єм мірного бачка, м³;

t – час заповнення мірного бачка, с.

Розраховують експериментальний коефіцієнт витрати отвору або насадка по формулі:

 = .

Значення коефіцієнта витрати, що були визначені дослідним шляхом для різних типів отворів і насадків, порівнюємо з теоретичними (обумовленими формулами 6.1, 6.3, 6.5), наведеними в таблиці 6.1.

Таблиця 6.2 - Результати вимірів

Таблиця 6.3 - Результати розрахунків

Зміст звіту

1. Короткі теоретичні відомості.

2. Схема лабораторної установки і її опис.

3. Таблиці вимірів і розрахунків.

4. Висновок.

Контрольні питання

1. Поясніть терміни «малий отвір», «тонка стінка», «насадок».

2. Доведіть, що коефіцієнти швидкості й витрати завжди менше одиниці.

3. Розкажіть про основні типи насадків (циліндричний зовнішній, циліндричний внутрішній, коноїдальний, конічний збіжний, конічний розбіжний).

4. Які коефіцієнти витрати для отворів у стінці й насадків?

5. Чому коефіцієнт витрати для насадка більше, ніж для отвору, у той час, як коефіцієнт швидкості менше?

Лабораторная работа № 1 приборы для измерения давления

Цель работы: изучить средства измерения давления и принципы их действия, приобрести практические навыки измерения давления.

1.1 Общие сведения

На жидкость действуют массовые и поверхностные силы. Массовые силы пропорциональны массе жидкости m (или объему жидкости V при ). Например, сила тяжести, сила инерции и др. Поверхностные силы пропорциональны площади поверхности , на которую они действуют. Например, сила трения, сила давления на поверхность и др.

Результирующую массовых и поверхностных сил можно разложить на составляющие: нормальную к поверхности ( ) и касательную к ней ( ). Направленная внутрь жидкости нормальная составляющая , действующая на поверхность , ограничивающую выделенный элемент жидкости, называется силой давления. Сжимающее напряжение, возникающее внутри жидкости под действием силы давления, называется гидростатистическим давлением.

Среднее гидростатистическое давление, т.е. сила, приходящаяся на единицу площади поверхности, определяется выражением

р_ср = .

Предел, к которому стремится это отношение при уменьшении поверхности , называется полным или абсолютным давлением в точке

р =

или

p = ,

где - элементарная сила, ;

- элементарная площадка, на которую действует сила , м².

В СИ основная единица измерения давления – Паскаль (Па); 1 Па = 1 . Внесистемные единицы измерения давления I мм рт. ст. (миллиметр ртутного столба) и I мм вод. ст. (миллиметр водяного столба) определяются давлением столба высотой h = 110^-3 м жидкости соответствующей плотности . Физическая атмосфера (1 атм) соответствует давлению столба ртути высотой 760 мм, техническая атмосфера (1 ат) – 735,8 мм.

1 мм вод. ст. = = 9,81 Па;

1 мм рт. ст. = 1 Торр = 133,3224 Па;

1 атм = 760 мм рт. ст. = 760 Торр = 101325 Па;

1 ат = = Па;

1 бар = 1 Па.

Если на жидкость действует только сила тяжести гидростатический закон распределения давления в однородной трудносжимаемой жидкости имеет вид:

р = р₀ + gh, (1.1)

где р  полное или абсолютное давление в рассматриваемой точке, Па;

р₀  давление на свободной поверхности (поверхностное или внешнее давление ), Па;

 относительное (или весовое давление), Па;

- глубина погружения рассматриваемой точки под уровень свободной поверхности, м.

Общий гидростатический закон: полное (абсолютное) давление в любой точке покоящейся жидкости равно внешнему давлению, сложенному с давлением столба жидкости высотой .

Закон Паскаля: давление на свободную поверхность передается во все точки покоящееся жидкости без изменений.

Следствие из закона Паскаля: на любой горизонтальной плоскости, пересекающей рассматриваемый покоящийся объем однородной жидкости или газа, давление постоянно.

Обычно в инженерной практике используют не абсолютное давление р , а его отклонение от атмосферного р_бар.

Если полное давление в рассматриваемой точке больше атмосферного, то разность ( ) представляет собой превышение абсолютного давления над атмосферным и называется манометрическим или избыточным давлением в данной точке:

р_изб = р_ман = р – р_бар = р₀ + gh – р_бар. (1.2)

Если давление на свободной поверхности жидкости равно атмосферному , то

р_изб = gh (1.2 а).

В этом случае избыточное и весовое давление совпадают.

Если абсолютное давление в рассматриваемой точке меньше атмосферного, то недостача полного давления до атмосферного называется вакуумом или разрежением:

р_вак = р_бар  р. (1.3)

Приборы для измерения давления весьма разнообразны. Они классифицируются по различным признакам.

По характеру измеряемой величины приборы разделяют на такие группы:

6. Приборы для измерения атмосферного давления - барометры.

7. Приборы для измерения разности абсолютного и атмосферного

давлений, т.е. избыточного и вакуумметрического давлений:

• манометры – приборы, измеряющие избыточное давление ;

• вакуумметры – приборы, измеряющие вакуум ;

• мановакуумметры – приборы, измеряющие и избыточное давление и вакуум.