1.3 Сигналы.

Сигнал представляет физическую величину, которая меняется со временем. Поэтому в качестве математической модели сигнала используется функция времени S(t). Свойства функции положены в основу классификации сигналов.

Классификация сигналов.

Классификация сигналов может быть проведена по разным признакам.

1. В основу классификации положены свойства множеств аргумента {t} и функции {S}. Графики соответствующих сигналов представлены на рис.1.7.

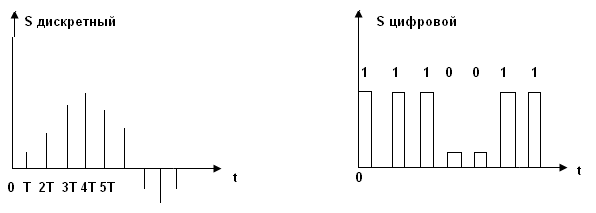
Рис.1.7

а) Сигнал аналоговый, если множество {t} и множество {S} непрерывны.

б) Сигнал дискретный, если множество {t} – дискретное, а множество {S}- непрерывное.

в) Сигнал квантованный, если множество {t} –непрерывное, а множество {S}- дискретное.

г) Сигнал цифровой, если множества {t} и {S}- дискретные.

Физически реализуемый сигнал всегда является дискретным. Дискретный сигнал моделирует отсчеты физического сигнала в моменты времени t_k. Обычно отсчеты берутся через одинаковые интервалы времени Т (интервал дискретизации по времени). Тогда t_k=kT, где k- номер отсчета. Квантованный (дискретный по уровню) сигнал можно трактовать как кусочно-непрерывное приближение реального сигнала. Если квант ΔS (интервал дискретизации по уровню) постоянная величина, то уровень S_m можно задать его номером m, т.е. S_m=mΔS. Отсчет цифрового сигнала задается парой чисел: k, m, которые соответствуют номерам отсчетов по времени и по уровню соответственно. Модель цифрового сигнала необходима, если радиосистема содержит узлы цифровой электроники.

1. Различают два больших классов сигналов: детерминированные и случайные. Для детерминированного сигнала S(t) в любой момент времени t точно известно значение S. Для случайного сигнала ξ(t) в момент времени t значение ξ – случайная величина. Детерминированные сигналы в свою очередь делятся на два подкласса: периодические и непериодические сигналы. Для периодического сигнала в любой момент t выполняется условие:

S(t) = S(t+nT), (1.14)

где n–целое число, T- период. Если не существует такого интервала времени T, для которого выполняется условие периодичности (1.9), то сигнал непериодический.

2. Сигнал является не только функцией времени, но также зависит от параметров – одного S(t) = S(t,λ), или нескольких S(t) = S(t, λ_1, λ₂,…).

Модуляция – это изменение параметра сигнала во времени. Изменение параметра должно быть медленным по сравнению с изменением самого сигнала. При наличии модуляции сигнал считается модулированным, при отсутствии – немодулированным. Для немодулированного сигнала параметр λ не зависит от времени.

Математическая модель сигнала должна отражать основные свойства реального сигнала и по возможности описываться простыми выражениями. Самыми распространенными моделями являются гармонический, или синусоидальный сигнал и прямоугольный импульс. Математической моделью гармонического сигнала является функция S(t)=cos(ωt+Ф). Математическая модель прямоугольного импульса представляет кусочно-непрерывную функцию времени S(t) = АП(t,);

, где δ длительность импульса.

График функции представлен на рис.1.8.

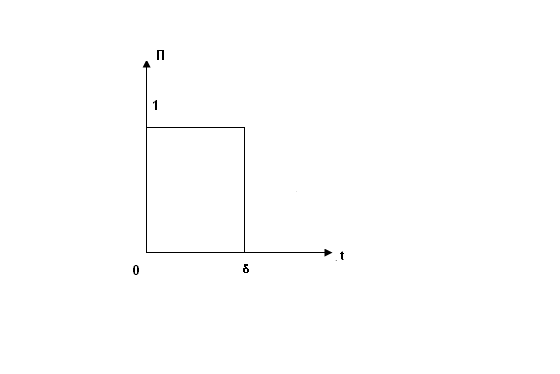
Рис.1.8

Линейные цепи при произвольных периодических воздействиях.

На практике приходится иметь дело с воздействиями более сложного типа, чем гармонический сигнал. Чтобы получить представление о принципах расчета цепей при произвольных периодических воздействиях, рассмотрим линейный двухполюсник, к которому прикладывается n-гармонических напряжений с различными амплитудами и кратными частотами колебаний, т.е. . Исследуемая цепь является линейной и к ней применим принцип суперпозиции. Согласно этому принципу ток, текущий в двухполюснике, равен сумме токов, возбуждаемых гармоническими напряжениями, т.е. . Поэтому расчет тока в цепи сводится к вычислению откликов на отдельные гармонические воздействия.

Если функция S(t)= S(t+nT), то ее можно разложить в ряд Фурье

(1.15)

а коэффициенты Фурье

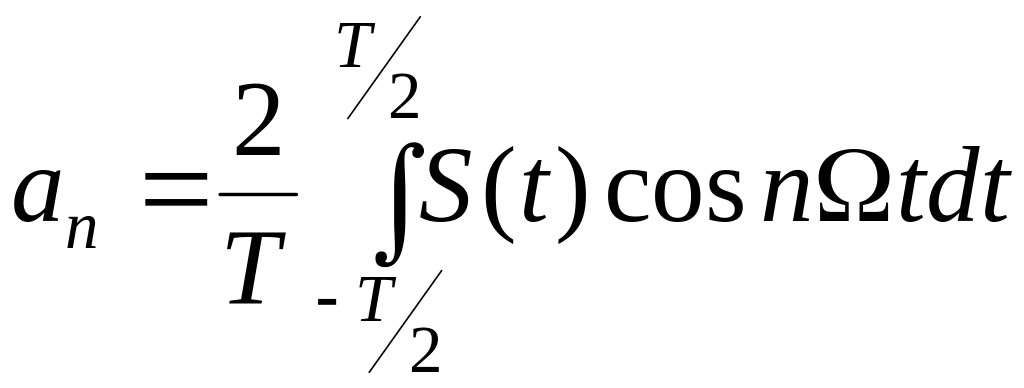, (1.16)

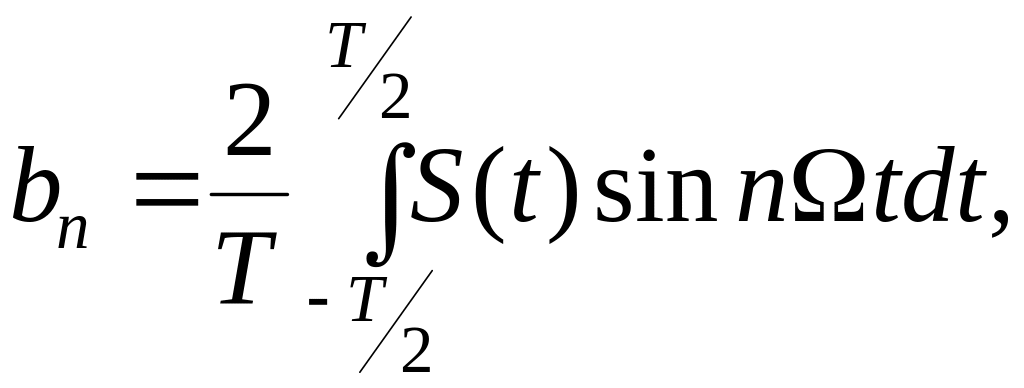(1.17)

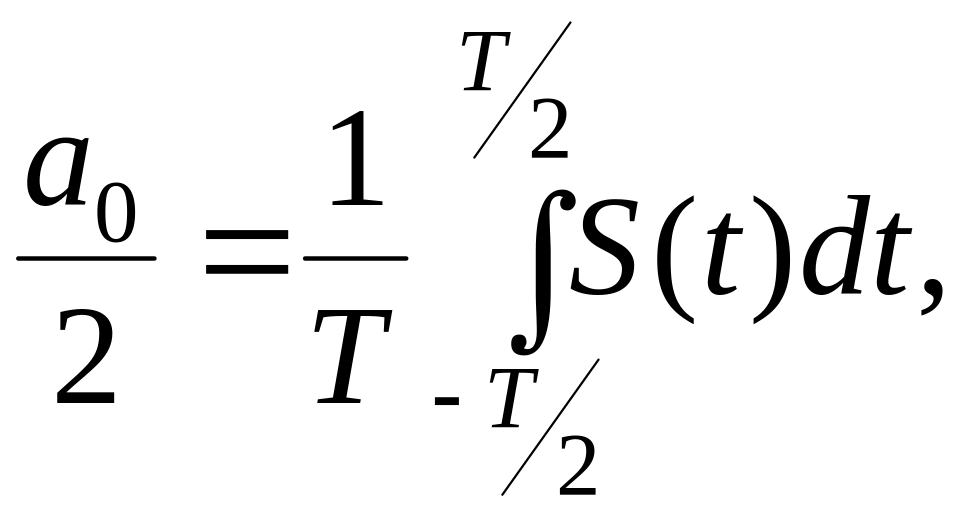(1.13)

где Ω=2π/T.

Разложение (1.10) можно представить в тригонометрической форме:

(1.18)

Здесь

(1.19)

(1.20)

Совокупность гармонических составляющих, на которые раскладывается функция S(t), называется спектром. Спектр периодической функции сложной формы, как вытекает из разложения (1.18) состоит из постоянной составляющей и множества гармонических составляющих, частоты которых образует дискретный ряд значений nΩ (n=1,2,3…), кратных основной частоте Ω. Амплитуды гармонических составляющих (или сокращенно гармоник) равны А_n, а начальные фазы φ_n. Такой спектр называется дискретным или линейчатым.

Заметим, что постоянную составляющую в разложении (1.18) можно рассматривать как гармонику с нулевой частотой колебания и амплитудой А₀=а₀/2.

В общем случае гармонические колебания, входящие в состав спектра, будут иметь различные амплитуды и фазы. Чтобы получить наглядное представление о спектре, целесообразно воспользоваться графиками – так называемыми спектральными диаграммами. Различают два типа диаграмм: амплитудные и фазовые, которые представлены на рис. 1.9 (амплитудная - а, фазовая -б).

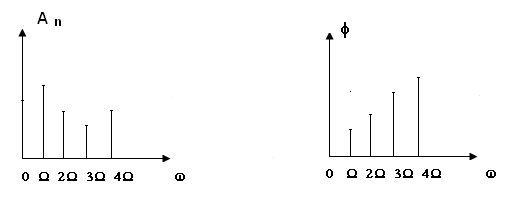
а) б)

Рис.1.9

Ряды Фурье могут быть записаны в комплексном виде. Известно, что

и

Подставляя эти выражения в разложение (1.15), после несложных преобразований получим

(1.21)

Воспользуемся далее обозначениями:

и .

Тогда вместо 1.21 будем иметь

.

Полагая и учитывая, что

приведем разложение S(t) к окончательному виду:

(1.22)

Равенство 1.18 есть комплексный ряд Фурье функции S(t).

Комплексный коэффициент Фурье с учетом выражений (1.16) и (1.17) определяется так:

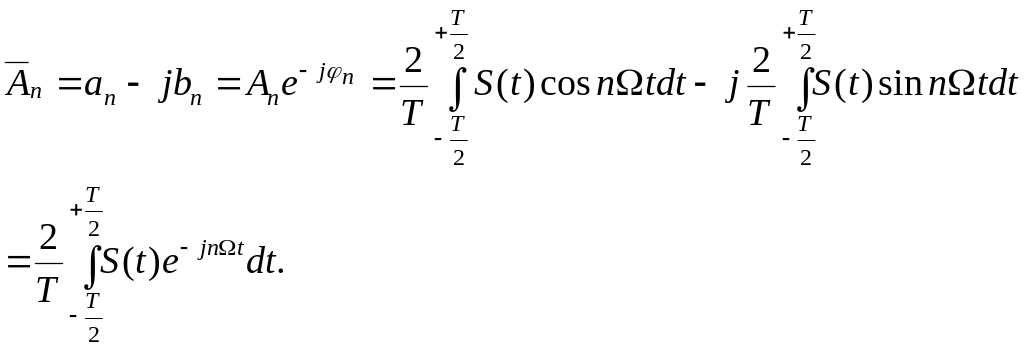(1.23)

В разложении 1.22 суммирование членов происходит как по положительным, так и по отрицательным n. Это означает, что комплексный ряд Фурье содержит гармоники не только с положительными, но и отрицательными частотами. Совершенно ясно, что последние частоты никакого физического смысла не имеют. Они появляются только как следствие формального представления тригонометрических функций с мнимым аргументом.

Очевидно, гармонические колебания с отрицательной частотой по аналогии с колебаниями, имеющими положительную частоту, можно представить в виде вектора, который вращается по плоскости с постоянной угловой частотой по часовой стрелке.

Найдем расстояния между соседними линиями спектра:

(n+1)Ω –nΩ = (n+1)2π/T -n 2π/T=2π/T.

При увеличении T это расстояние уменьшается, и спектр становится более плотным. От величины T зависят также амплитуды гармонических составляющих спектра. Зависимость комплексных амплитуд гармонических составляющих от частоты (если ω рассматривать как непрерывную переменную) определяется функцией

(1.24) которая не содержит T и носит название спектральной функции.

Из выражений (1.23) и (1.24) вытекает, что

если . (1.24а)

Ряды четных и нечетных функций.

Рассмотрим некоторые особенности рядов Фурье при дополнительных условиях, накладываемых на функцию S(t). Пусть S(t) – четная функция, т.е. S(-t)= S(t) (рис.1.10а).

При таком условии коэффициенты Фурье принимают вид

(1.25)

и

Следовательно, в разложении (1.25) останутся только те члены, содержащие косинусоидальные функции

(1.26)

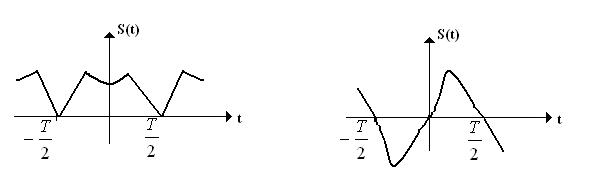
а) б)

Рис. 1.10

Если S(t) – нечетная функция т.е. S(-t)= -S(t) (рис.1.10б), то и

. (1.27)

Ряд Фурье в этом случае имеет только синусоидальные составляющие:

(1.28)

Спектральное представление непериодических сигналов.

В теории спектрального представления непериодических (импульсных) сигналов используют искусственный прием, формально заменяя такие сигналы периодическими с бесконечно большим периодом следования Т→∞.

Положим, что некоторая заданная функция S(t) аналитически описывает одиночный импульсный сигнал конечной длительности. Мысленно дополнив его такими же импульсными сигналами, следующими с некоторым интервалом Т, получим периодическую последовательность аналогичных импульсов S_n(t)= S(t+nT).

Для того чтобы вне искусственного интервала 0, Т исходный сигнал был равен нулю, необходимо увеличить период повторения импульсов. В пределе, при увеличении периода и Т→∞, все импульсы уйдут вправо и влево в бесконечность и периодическая последовательность S(t) вновь станет одиночным импульсом. В этом случае выражения (1.9.), (1.10) по-прежнему должны сохранять свой смысл, однако угловая частота Ω=2π/Т теперь будет стремиться к нулю, и ее придется заменить бесконечно малой величиной dω. Далее, произведение nΩ при Т→∞., очевидно, может принимать любые значения и является непрерывной функцией n. Поэтому nΩ следует рассматривать как текущую частоту ω, изменяющуюся от -∞ до +∞. Легко заметить, что при увеличении периода следования импульсов Т линейчатый спектр будет все более плотным. В предельном случае, когда Т→∞., равные расстояния между спектральными линиями уменьшатся настолько, что спектр станет сплошным, а амплитуда отдельных спектральных составляющих окажутся бесконечно малыми.

С учетом последних соотношений коэффициент для бесконечно большого интервала разложения будет равен

где

(1.29)

Отсюда вытекает, что при вычислении S(t) вместо суммирования дискретных значений e^jnΩt в (1.9) необходимо складывать бесконечно малые величины d (ω)e^jωt с частотой, изменяющейся непрерывно. Другими словами, ряд (1.9) превращается в интеграл

. (1.30)

Выражения (1.29) и (1.30) представляют собой прямое и обратное преобразование Фурье.

Итак, из равенств (1.29) и (1.30) видно, что любую непериодическую функцию S(t) можно представить в виде бесконечного множества гармонических составляющих, частоты которых образуют непрерывное множество значений от -∞ до +∞.

Совокупность гармоник, как известно, составляет спектр заданной функции S(t). В рассматриваемом случае каждая гармоника имеет бесконечно малую комплексную амплитуду. Поэтому в качестве спектральной характеристики процесса используется функция , называемая спектральной плотностью непериодической функции S(t). Она определяет соотношение между комплексными амплитудами гармоник в спектре.

Если S(t) отлична от нуля на конечном интервале, спектральная плотность ее совпадает со спектральной функцией, ранее введенной в теории рядов.

Спектральная плотность есть функция комплексная. Из выражения (1.29) видно, что

(1.31)

где

(1.32)

(1.33)

Модуль спектральной плотности равен

. (1.34)

и является четной функцией переменной ω, т.е. F(-ω)= F(+ω).

Аргумент

(1.35)

Таким образом, спектр непериодической функции характеризуется зависимостью модуля F(ω) и аргумента φ(ω) спектральной плотности.

Отметим связь между значениями спектральной плотности одиночного импульса и амплитудами гармонических составляющих периодической последовательности таких импульсов. Для этого сравним выражение (1.24а) комплексных амплитуд гармонических составляющих периодической последовательности импульсов с периодом Т со спектральной плотностью одиночного импульса той же последовательности (1.29), если импульс существует в промежутке –Т/2 до +Т/2:

. (1.36)

Некоторые свойства преобразований Фурье.

Рассматриваемые далее свойства преобразований Фурье позволяют наиболее просто по заданной непериодической функции S(t) находить ее спектральную плотность F(jω) или по заданной спектральной плотности F(jω) находить оригинал, т.е. функцию S(t).

1. Свойство линейности. При преобразованиях Фурье вследствие их линейности может быть использован принцип суперпозиции, в силу которого суммирование временных функций соответствует суммированию их спектральных функций. Если

и , то

. (1.37)

(Знак означает соответствие).

2. Изменение масштаба функции. Если

, то . (1.38)

3. Теорема подобия. Если

то . (1.39)

Следовательно, увеличение длительности импульса вызывает сжатие его спектральной плотности и уменьшение амплитуд гармонических составляющих спектра, т.е. ширина полосы пропускания должна быть тем больше, чем короче передаваемый импульс.

4. Теорема запаздывания. Если

, то . (1.40)

Согласно этой теореме запаздывание функции на время t₀ вызывает смещение фазового спектра функции на угол ωt_0, но амплитудный спектр не изменяется.

С помощью теоремы запаздывания может быть найдена спектральная плотность последовательности одинаковых импульсов, если известна спектральная плотность одного импульса.

5. Теорема смещения. Если

, то (1.41)

Умножение сигнала на комплексную амплитуду е^jω₀^t приводит к сдвигу спектра сигнала по оси частот на величину ω₀ в сторону увеличения частот. На основании свойства смещения спектра функции можно найти спектры отрезков синусоид и косинусоид по известным спектрам огибающих этих гармонических функций. Например, пусть задана функция S(t)cosω₀t и известно, что . Преобразуем заданную функцию, записав cosω₀t в показательной форме:

(1.42)

Согласно предыдущему спектральная плотность заданной функции будет иметь вид

(1.43)

6. Дифференцирование временной функции. Если

, то (1.44)

Дифференцирование сигнала по времени соответствует умножению спектральной плотности на jω.

7. Интегрирование временной функции. Если

, то (1.45)

Интегрирование сигнала по времени соответствует делению спектральной плотности на jω.

8. Энергетическое соотношение. Для сигнала с непрерывным спектром:

(1.46)

Если учесть четность амплитудного спектра, то правый интеграл запишется по положительным, физически реализуемым, частотам

(1.48)

Энергия сигнала с непрерывным спектром определяется только амплитудным спектром и не зависит от фазового спектра.

Спектры некоторых непериодических функций.

В качестве примера найдем спектр одиночного прямоугольного импульса, график которого представлен на рис.1.11.

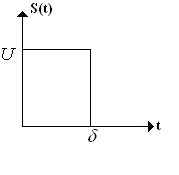
Рис.1.11

Запишем выражение для функции S(t):

(1.49)

Функцию спектральной плотности найдем, используя соотношение (1.29).

(1.40)

Чтобы обойти громоздкие вычисления амплитудного и фазового спектров, проведем преобразование числителя:

Умножим на δ числитель и знаменатель выражения (1.40). После этих преобразований функция спектральной плотности принимает удобную для анализа форму:

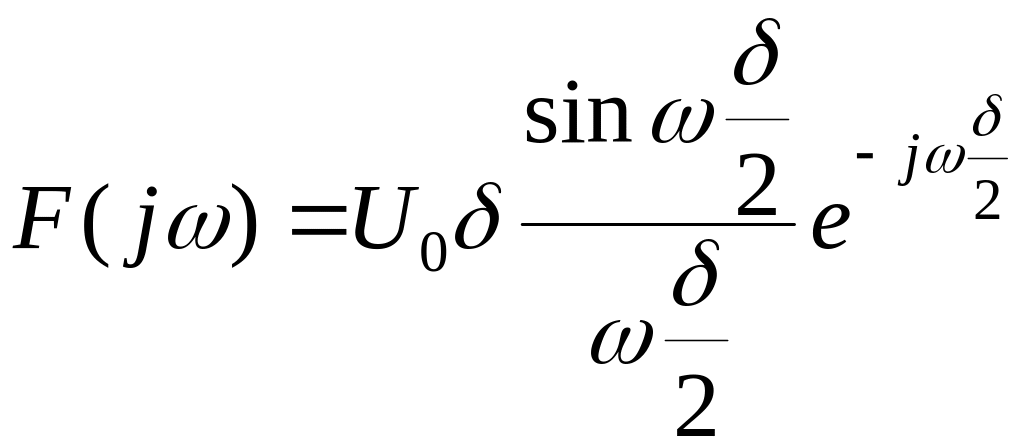. (1.41) Отсюда нетрудно найти амплитудный спектр:

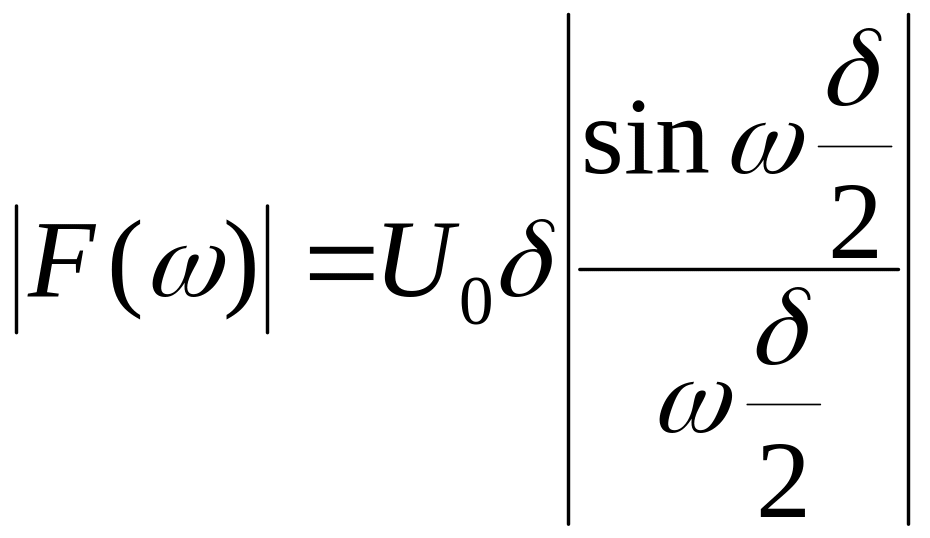(1.42)

Сравнивая (1.41) и (1.23), можно записать фазовый спектр:

(1.43)

где - целая часть от выражения в обратных скобках.

Графики амплитудного и фазового спектров приведены на рис.1.4. (Б.2.9 стр.52)

Амплитудная спектральная плотность максимальна на нулевой частоте. На частотах

(1.44)

амплитудная спектральная плотность равна нулю.