3.4. Частотные характеристики и частотные функции цепей.

В теории радиотехнических цепей особое внимание уделяется изучению их свойств при гармонических воздействиях с различными частотами.

Какова бы не была схема цепи, она может быть изображена в виде пассивного многополюсника (рис.3.3), из которого выделены во внешние относительно него участки цепей: источники воздействия и те пассивные элементы, отклики в которых подлежат определению.

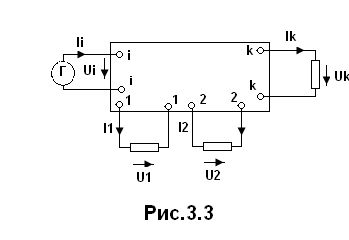
Зажимы многополюсника, к которым подключены источники, называются входными.

Пары зажимов между которыми могут быть включены внешние пассивные элементы, называются выходными.

Пусть цепь находится под гармоническим воздействием (напряжения или тока), выражаемым текущим комплексом ; источник воздействия включен, например, между зажимами i – i. Текущий комплекс отклика некоторой (k-й) ветви .

Комплексной частотной характеристикой цепи (КЧХ) называется отношение текущих комплексов отклика и воздействия.

Так как цепь неизбежно

содержит реактивные элементы, параметры которых зависят от частоты, то КЧХ в общем случае является комплексной функцией частоты. Будем обозначать ее :

(3.6)

Таким образом, КЧХ представляет собой отношение комплексных амплитуд отклика и воздействия . В последних выражениях - амплитуды отклика и воздействия; - соответственно их начальные фазы. Следует помнить, что размерность частотной характеристики равна отношению размерностей и .

Записав в показательной форме, получим

(3.7)

Здесь - амплитудно-частотная характеристика (АЧХ);

- фазо-частотная характеристика (ФЧХ).

Таким образом, КЧХ сочетает в себе две характеристики:

а) АЧХ, определяющую зависимость от частоты амплитуд отклика и воздействия;

б) ФЧХ. выражающую сдвиг фаз между откликом и воздействием как функцию частоты.

Амплитудно-частотные фазо-частотные характеристики могут быть представлены графиками или таблицами числовых значений, полученными, например, экспериментально.

Аналитическое выражение комплексной частотной характеристики называется комплексной частотной функцией.

Частотные функции классифицируются в зависимости от того, какие конкретные величины понимаются под воздействием и откликом. В частности, функции подразделяются на входные и передаточные.

а. Входные функции

Пусть требуется определить отклик на входе цепи, т.е. ток при заданном напряжении (или при заданном ). Схема, изображенная на рис. 3.7 стр105, в этом случае сводится к двухполюснику (рис.3.4)

Когда отклик и воздействие рассматриваются на одной паре зажимов i-i, то частотная характеристика и соответствующая ей функция называется входной.

Входная частотная функция имеет размерность сопротивления. Очевидно, что она является входным сопротивлением между точками i-i:

(3.8)

Другая входная функция имеет размерность проводимости и совпадает с понятием проводимости цепи:

(3.9)

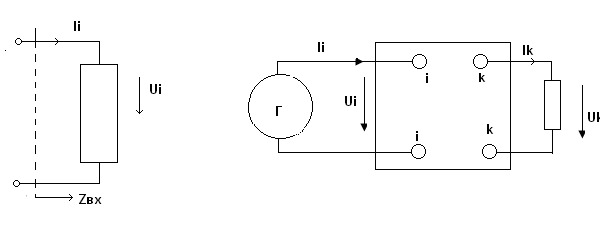
Рис.3.4 Рис.3.5

б. Передаточные функции

Когда требуется определить отклик на одном из выходов (k-k) на воздействие источника, включенного на входе цепи (i-i), схема, изображенная на рис.3.3, может быть представлена в виде четырехполюсника (рис.3.5). Соответствующая такой постановке задачи комплексная частотная характеристика (функция) называется передаточной.

Возможны четыре разновидности передаточных функций.

1. Определению подлежит ток 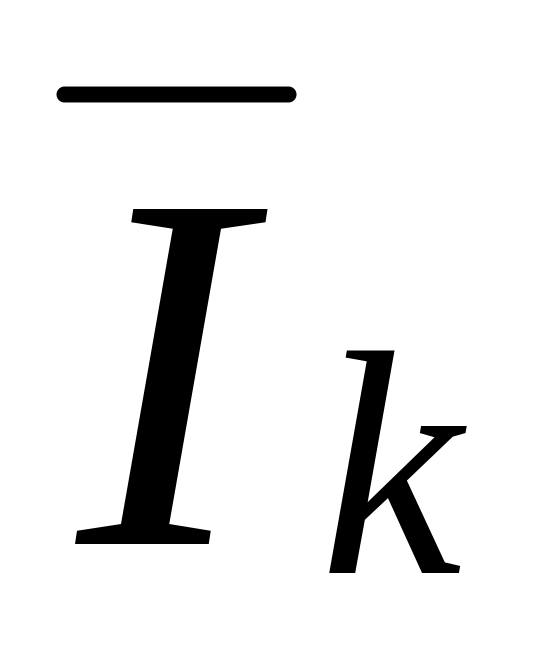при заданном напряжении .

Частотная функция в этом случае имеет размерность проводимости и носит наименование передаточной проводимости.

2. Искомым является напряжение 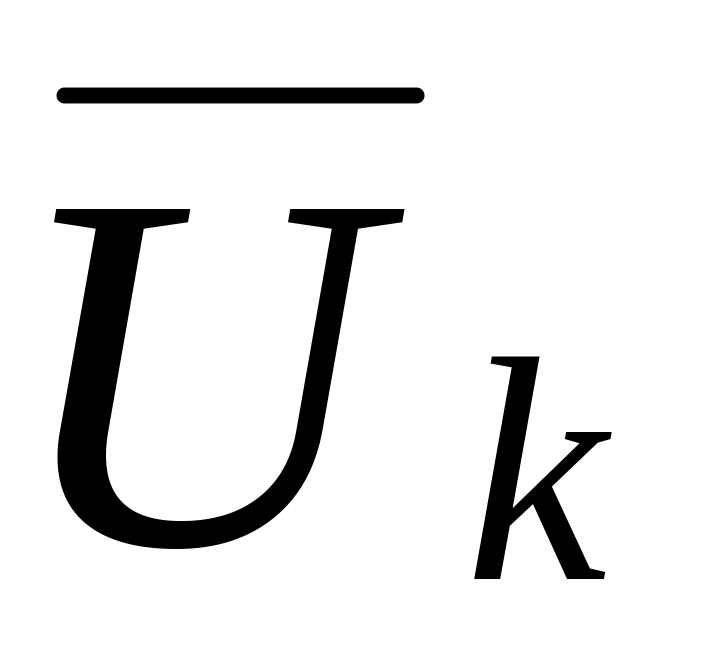при заданном токе . Тогда частотная функция имеет размерность сопротивления и называется передаточным сопротивлением.

3. Требуется рассчитать ток при известном токе . Теперь частотная характеристика безразмерна и носит название передаточная функция по току.

4. Задача заключается в определении выходного напряжения при заданном напряжении на входе . В этом случае функция безразмерна и называется передаточной функцией по напряжению.

Значение ,найденное для определенной частоты, называется комплексным коэффициентом передачи по напряжению.

в. Делитель напряжения. Компенсированный делитель напряжения.

Для уменьшения уровня сигнала, подаваемого на какое либо устройство, применяют делитель напряжения, общая схема которого представлена на рис 3.6.

Рассчитаем передаточную функцию по напряжению.

; , Окончательно получаем

(3.10)

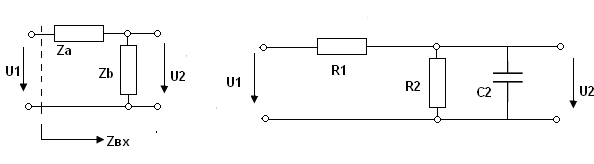
Рис.3.6 рис.3.7

Если в схеме нет реактивных элементов, т.е. , , то коэффициент передачи делителя напряжения не зависит от частоты и определяется как

. (3.11)

Однако, как правило, паразитные емкости (например, входная емкость осциллографа) превращают такой делитель в частотнозависимую цепь (рис.3.7).

Действительно, как видно из рис.3.7, коэффициент передачи такой цепи будет комплексным

. (3.12)

Для того чтобы исключить возникающие искажения, параллельно сопротивлению R₁ включают емкость C₁ (рис.3.8).

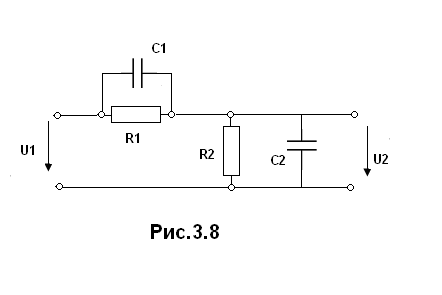
Для такой схемы комплексный коэффициент передачи найдется как

. (3.13)

Путем несложных преобразований получаем

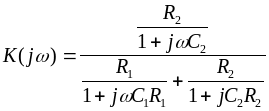. (3.14)

Если выполнено условие R₁C₁=R₂C₂ , то коэффициент передачи не зависит от частоты и равен

. (3.15)

г. Частотные характеристики цепей с одним энергоемким элементом.

Произведем расчет передаточной функции цепи в предположении, что в качестве энергоемкого элемента использована емкость, с которой снимается напряжение (рис.3.9).

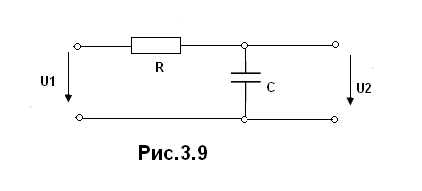
В общем случае передаточная функция четырехполюсника

(3.16)

Здесь , - начальные фазы напряжений u₂, u₁соответственно; ; .

Подставив в (3.16) , , найдем

(3.17)

Амплитудно-частотная характеристика

(3.18)

Фазо-частотная характеристика

(3.19)

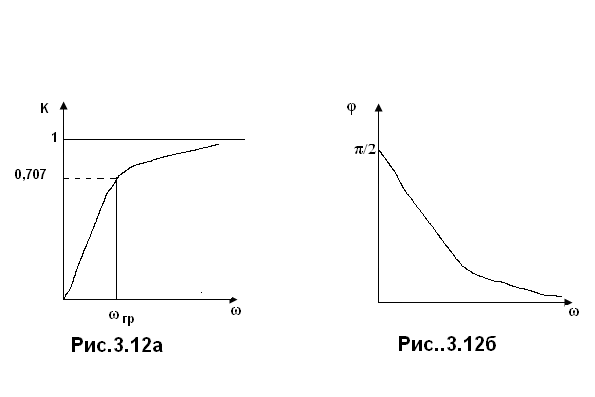
На рис. 3.11а изображен график АЧХ, а на рис.3.11б – кривая ФЧХ.

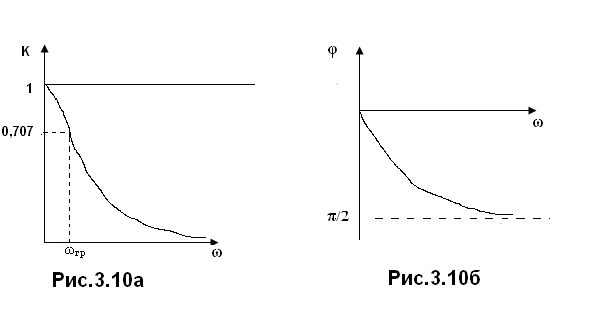
Как видно рассматриваемый четырехполюсник пропускает частоты, меньше ω_гр=1/RC, и подавляет более частоты. Такая цепь называется интегрирующей. Поменяв местами R и C, соответственно получим дифференцирующую цепь (рис.3.11),

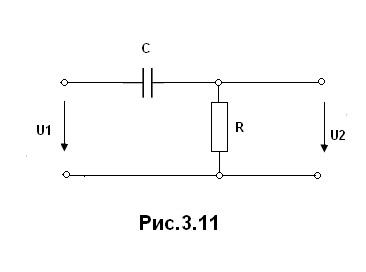
для которой АЧХ запишется как

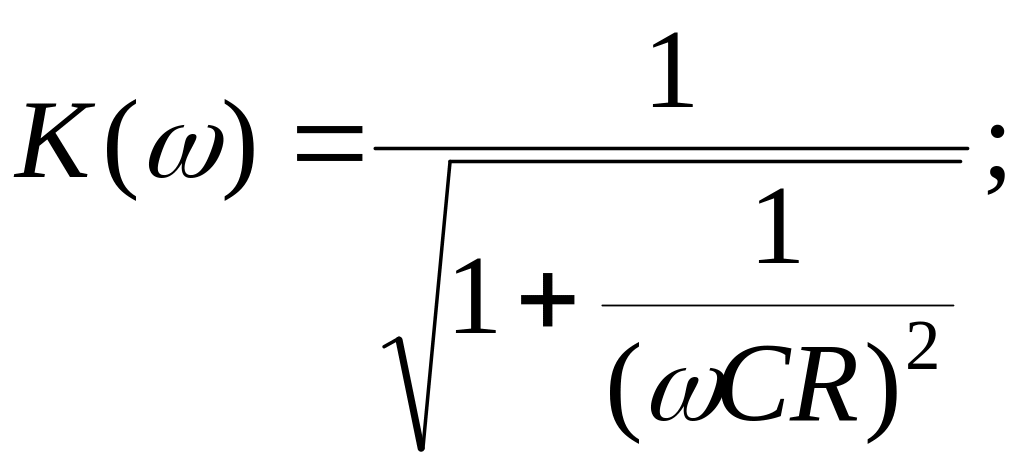(3.19)

а ФЧХ

(3.20)

Графики АЧХ и ФЧХ представлены на рис. 3.12.

34