2. 4. Метод Эйлера.

Иногда этот метод называют методом Рунге-Кутта первого порядка точности.

Данный метод одношаговый. Табулирование функции происходит поочередно в каждой точке. Для расчета значения функции в очередном узле необходимо использовать значение функции в одном предыдущем узле.

Пусть дано дифференциальное уравнение первого порядка:

Y’ = f(x, y)

с начальным условием

y(x₀) = y₀

Выберем шаг h и введём обозначения:

x_i = х₀ + ih и y_i = y(x_i), где i = 0, 1, 2, ...,

x_i - узлы сетки,

y_i - значение интегральной функции в узлах.

Иллюстрации к решению приведены на рисунке 2.

Проведем прямую АВ через точку (x_i, y_i) под углом α. При этом tg α = f(x_i, y_i)

В соответствий с геометрическим смыслом задачи, прямая АВ является касательной к интегральной функции. Произведем замену точки интегральной функции точкой, лежащей на касательной АВ.

Тогда y_i+1 = y_i + Δy

Из прямоугольного треугольника ABC

Приравняем правые части tg α = f(x_i, y_i) и . Получим

Отсюда Δу = h ∙ f(x_i, y_i).

Подставим в это выражение формулу y_i+1 = y_i + Δy, а затем преобразуем его. В результате получаем формулу расчета очередной точки интегральной функции:

.

Рисунок 2. Метод Эйлера.

Из формулы видно, что для расчета каждой следующей точки интегральной функции необходимо знать значение только одной предыдущей точки. Таким образом, зная начальные условия, можно построить интегральную кривую на заданном промежутке.

Блок-схема процедуры решения дифференциального уравнения методом Эйлера приведена на рисунке 3.

Eiler(X0, Xk, Y0, N, Y)

F(x, у) - заданная функция – должна

б

h = (Xk – X0)/N

ыть описана отдельно.

Входные параметры:

Х

i = 0, …, N - 1

0,XK—начальное и конечное

значения независимойпеременной;

Y

x = X0 + i ∙ h

0 – значение y₀ из начального условия

y(x₀) = y₀;

N

Y_i+1 = Y_i + h ∙ F(x, Y_i)

- количество отрезков разбиения;

Выходные параметры:

У - массив значений искомого решения

в

End

узлах сетки.

Рисунок 3. Блок-схема процедуры решения дифференциального уравнения методом Эйлера.

Метод Эйлера - один из простейших методов численного решения обыкновенных дифференциальных уравнений. Но существенным его недостатком является большая погрешность вычислений. На рисунке 2 погрешность вычислений для i-гo шага обозначена ε. С каждым шагом погрешность вычислений увеличивается.

2.5.Метод Рунге - Кутта 4-го порядка

Пусть дано дифференциальное уравнение первого порядка

y' = f(x,y)

с начальным условием:

y(x₀) = y₀

Выберем шаг h и введём обозначения:

x_i = x₀ + ih и y_i = y(x_i), где i = 0,1, 2, ....

Аналогично описанным выше методам производится решение дифференциального уравнения. Отличие состоит в делении шага на 4 части.

Согласно методу Рунге - Кутта четвёртого порядка, последовательные значения y_i искомой функции у определяются по формуле:

y_i+1 = y_i + Δy_i

где

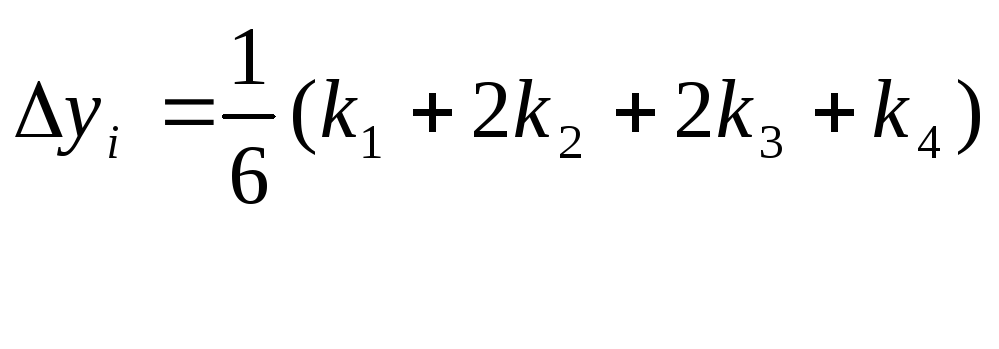, i = 0, 1, 2, …

а числа k₁⁽ⁱ⁾, 2k₂⁽ⁱ⁾, 2k₃⁽ⁱ⁾, k₄ ⁽ⁱ⁾ на каждом шаге вычисляются по формулам:

Это явный четырехэтапный метод четвертого порядка точности.

Методы Рунге - Купа легко программируются и обладают значительной точностью и устойчивостью для широкого круга задач.

На рисунке 6 приведена блок-схема процедурыRUNGE(X0, XK, Y0, N, Y) для решения задачи Коши описанным выше методом Рунге - Кутта.

F(x, у)- заданная функция - должна

быть описана отдельно.

Входные параметры:

ХО, ХК. - начальное и конечное

значения независимой

переменной;

Y0 - значение у₀ из начального условия

N—количество отрезков разбиения;

Выходные параметры:

Y - массив значений искомого решения

в узлах сетки;

Рисунок б. Блок-схема процедуры RUNGE

На рисунке 7 приведена блок-схема алгоритма основной программы для решения задачи Коши и получения результатов с фиксированным количеством отрезков разбиения N. В основной программе происходит обращение к процедуре RUNGE(X0, ХК, Y0, N, Y), вычисляющей значения искомой функции у_i в точках х_i методом Рунге - Кутта.

Исходными данными в данной задаче являются:

Х0, ХК - начальное и конечное значения независимой переменной;

Y0 - значение у₀ из начального условия у(х₀) = у₀;

N - количество отрезков разбиения.

Результаты работы программы выводятся в виде двух столбцов: X - массив значений узлов сетки; Y - массив значений искомого решения в соответствующих узлах сетки.

Рисунок 7. Блок-схема алгоритма основной программы для решения задачи Коши с фиксированным количеством отрезков разбиения N