Вычислительная геометрия
Лекция 5
•Геометрический поиск. Метод локусов
•Методы локализации точки
•Метод полос
•Метод цепей
•Метод детализации триангуляции
Геометрический поиск
Абстрактная модель поиска:
некоторый набор данных – «файл»;
некоторый новый элемент данных – «образец».
Поиск – установление связи между образцом и файлом.
Геометрический поиск
•Файлы – сложные геометрические структуры: множества точек, многоугольники, графы и т.п.
•Образцы: точки, регионы и т.п.
Запрос на поиск (на обработку – просмотр файла) Пример: поиск в массиве чисел.
Уникальный запрос. Массовый запрос.
Предобработка – структуризация данных (сортировка)
30.03.2007 |
Геометрический поиск |
2 |
|
Локализация точки |
|
Геометрический поиск
4 меры оценки ресурсов
при анализе геометрических алгоритмов поиска:
• Время предобработки. Сколько времени
необходимо для организации данных перед поиском?
• Время запроса. Сколько времени необходимо для ответа на один запрос?
• Память. Сколько памяти необходимо для структуры данных (СД)?
• Время корректировки. Предъявлен элемент
данных. Сколько времени потребуется на его включение в СД или исключение из неё?
30.03.2007 |
Геометрический поиск |
3 |
|
Локализация точки |
|
Фазы обработки при геометрическом поиске
Элемент(ы) файла ИД
Корректировка
СД
образец
Предобработка |
|
Обработка |
Файл |
Файл |
запроса |
|
||
|
|
|
|
(СД) |
|
Ответ
30.03.2007 |
Геометрический поиск |
4 |
|
Локализация точки |
|
Пример: бинарный поиск в массиве из n элементов
•Время предобработки: сортировка
–O (n log n)
• Время запроса: log2 (n + 1) или
O(log n)
•Память: O (n)
•Время корректировки: O (n)
30.03.2007 |
Геометрический поиск |
5 |
|
Локализация точки |
|
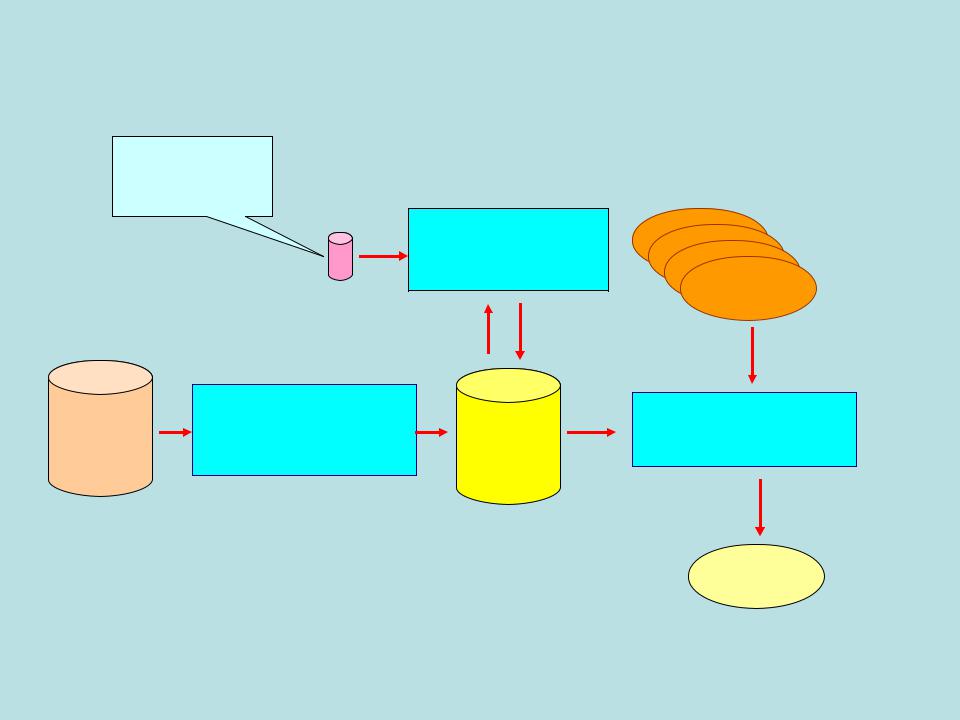
Региональный поиск (подсчет).
Региональный поиск: даны n точек на плоскости.
Сколько из них лежит внутри заданного прямоугольника, стороны которого параллельны координатным осям?
Т.е. сколько точек p = (x, y) удовлетворяют неравенствам a x b, c y d для заданных a, b, c и d ?
В форме отчет – перечислить внутренние точки.
Уникальный региональный запрос – O(n) (оптимально).
Метод локусов. Локус –
геометрическое место точек, в пределах которого ответ не меняется.
30.03.2007 |
Геометрический поиск |
6 |
|
Локализация точки |
|
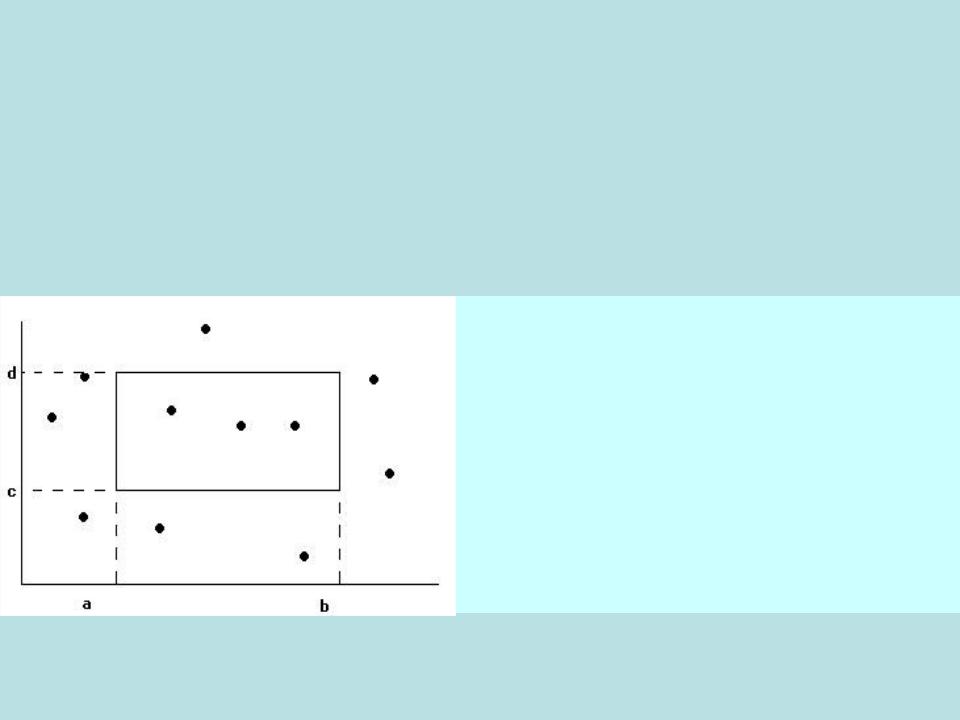
Региональный поиск. Метод локусов
Прямоугольник = 4 вершины.
Можно заменить запрос с прямоугольником четырьмя подзадачами, по одной на каждую из его вершин.
Подзадача, связанная с вершиной p: определить число точек Q(p) исходного множества, которые удовлетворяют неравенствам x x(p) и y y(p), т.е. числа точек в левом нижнем квадранте, определяемом вершиной p.
векторное доминирование
Говорят, что точка (вектор) v доминирует над w, тогда и только тогда, когда для всех индексов (координат) i верно условие vi wi. На плоскости точка v
доминирует над w тогда и только тогда, когда w лежит в левом нижнем
квадранте, определяемом v.
Сколько точек “юго-западнее” p?
30.03.2007 |
Геометрический поиск |
7 |
|
Локализация точки |
|
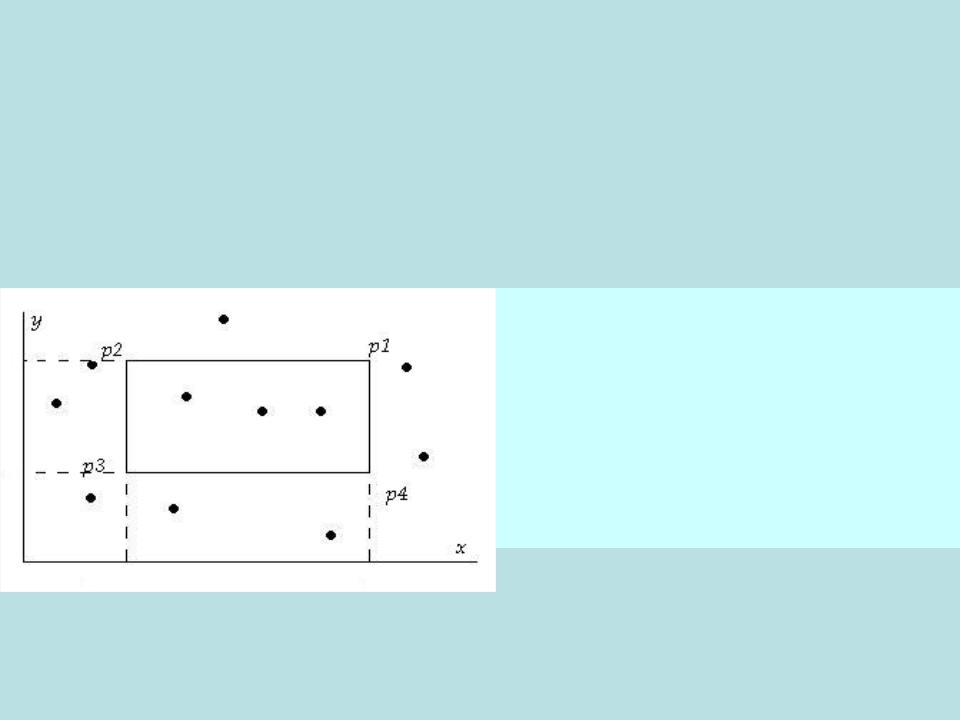
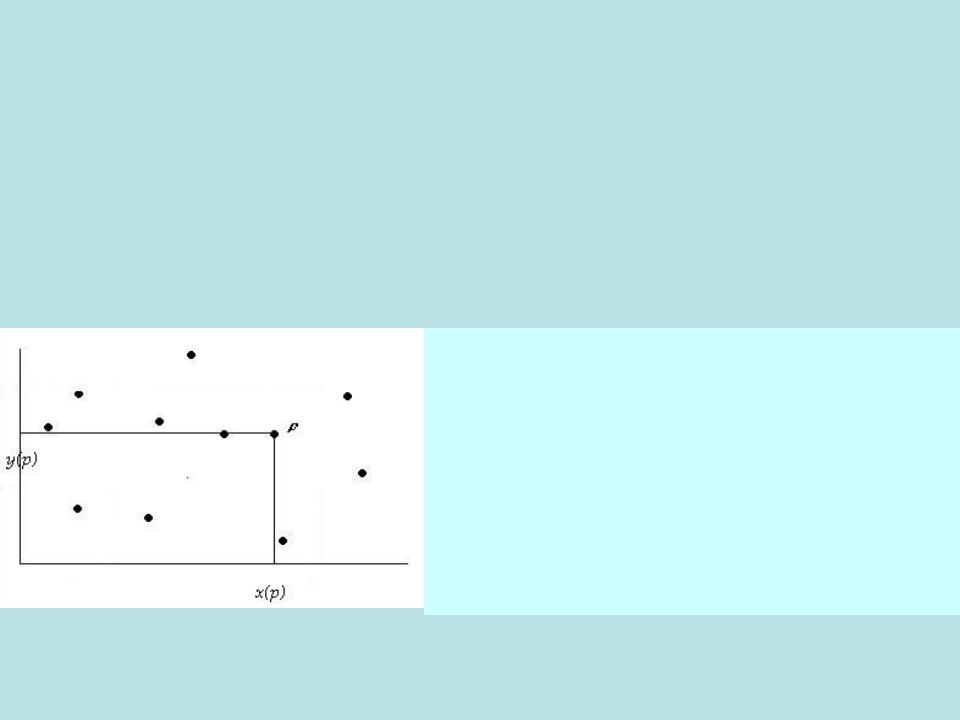
Региональный поиск. Метод локусов
Связь между доминированием и региональным поиском
Число точек N(p1p2p3p4) в прямоугольнике p1p2p3p4 определяется следующим образом:
N(p1p2p3p4) = Q(p1) - Q(p2) - Q(p4) + Q(p3)
На плоскости существуют области удобной формы, внутри которых число
доминирования Q является константой. Локусы.
См. папку «1Метод локусов»
30.03.2007 |
Геометрический поиск |
8 |
|
Локализация точки |
|
Региональный поиск. Метод локусов
Из точек p опущены перпендикуляры на оси x и y, а полученные линии продолжены в бесконечность. Они создают решетку из (n+1)2 прямоугольников.
0 |
1 |
2 |
3 |
4 |
5 |
0 |
0 |
1 |
2 |
3 |
4 |
0 |
0 |
1 |
2 |
2 |
3 |
0 |
0 |
1 |
1 |
1 |
2 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
30.03.2007 |
|
Геометрический поиск |
9 |
||
|
|
Локализация точки |
|
||
Региональный поиск. Метод локусов
Предобработка: сортировка O(n log n) + решетка O(n3) O(n2) Запрос: 2 бинарных поиска O(log2n)
Метод
Без
предобработки
Метод
локусов
Метод дерева регионов
Запрос Память Предобработка
O(n) |
O(n) |
O(n) |
O(log n) |
O(n2) |
O(n2) |
O(log2 n) O(n log n) |
O(n log n) |
Локализация точки